Конспект лекций 7

Вычисление обратной матрицы

Пусть A = (a_ij) – квадратная матрица с определителем, не равным нулю. Тогда существует обратная матрица A^–1, которая вычисляется по формуле

.

Последняя формула означает, что в i-й строке и j-м столбце обратной матрицы располагается алгебраическое дополнение элемента, стоящего в j-й строке и в i-м столбце исходной матрицы, деленное на определитель исходной матрицы.

Напомним здесь, что A_pq = (–1)^p+qM_pq, где M_pq называется минором и представляет собой определитель, получающийся из определителя detA вычеркиванием p-й строки и q-го столбца.

Если определитель матрицы равен нулю, матрица называется вырожденной.

Пример 1. Построить матрицу, обратную к заданной матрице

.

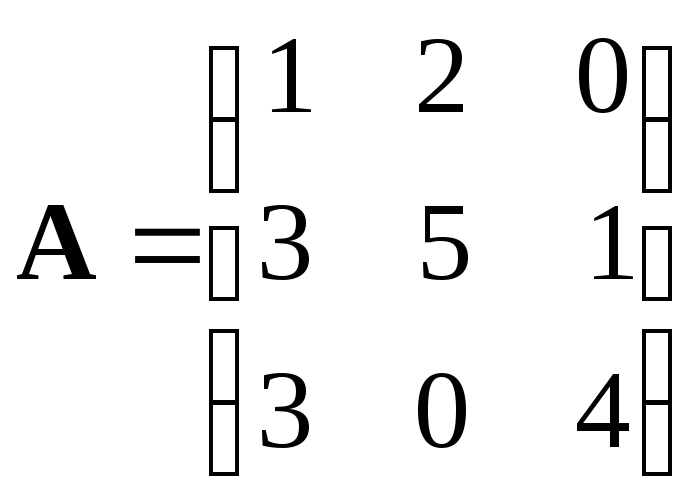Вычислим детерминант матрицы: detA = 20 + 6 – 24 = 2.

Построим матрицу , каждый элемент которой есть алгебраическое дополнение соответствующего элемента матрицы А:

.

Транспонируем полученную матрицу: .

Выпишем обратную матрицу: .

Пример 2. Проверьте равенства AA^–1 = A^–1A = E в предыдущем примере.

.

Правило Крамера решения квадратных систем линейных уравнений

Пусть задана квадратная система линейных уравнений:

.

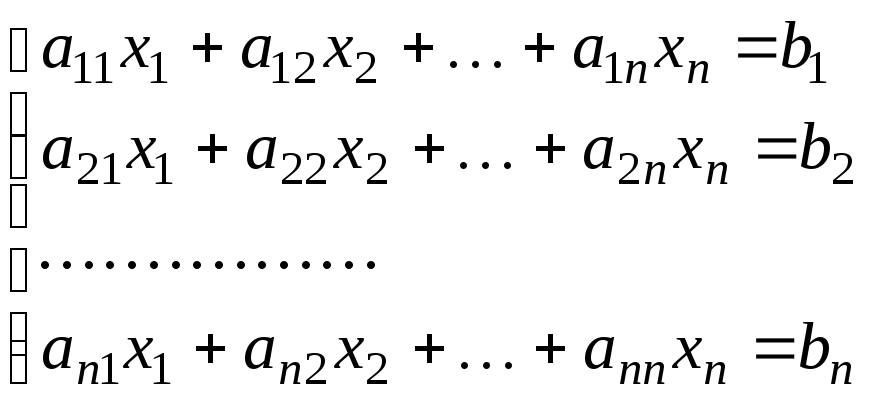Ее можно записать в матричной форме: AX = B, где

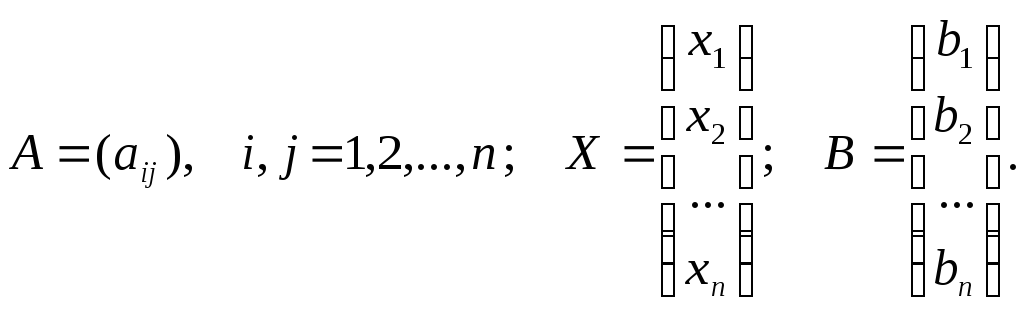
Если определитель матрицы A не равен нулю, то система имеет единственное решение, определяемое формулами:

.

Здесь  – определитель n-го порядка матрицы A коэффициентов системы, _i – определитель n-го порядка, получающийся из определителя  матрицы A коэффициентов системы заменой i-го столбца столбцом свободных членов.

Пример 1.

.

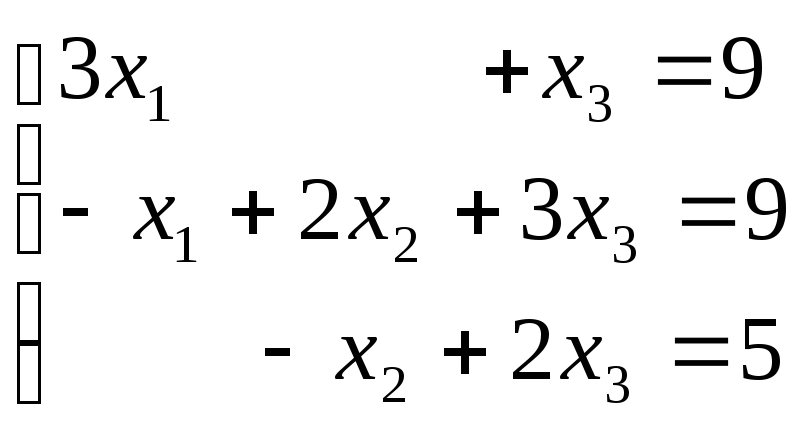Вычислим соответствующие определители:

Выпишем решение системы:

Отметим, что если определитель матрицы А коэффициентов квадратной системы линейных уравнений равен нулю, то возможен один из двух случаев: либо система несовместна, либо она совместна и неопределенна.

Матричные уравнения

Уравнения вида A*X=B, X*A=B, A*X*B =C называются матричными.

Решим первое. Помножив обе части уравнения слева на матрицу, обратную к матрице A, получим A^-1*A*X=A^-1*B. По определению обратной матрицы A^-1*A= E, следовательно, E*X=A^-1*B. По определению единичной матрицы E *X = X, тогда X=A^-1*B.

Аналогично решаются второе и третье уравнения:

X*A*A^-1=B*A^-1, X*A*A^-1=B*A^-1, X*E=B*A^-1, X=B*A^-1;

A*X*B=C, A^-1*A*X*B*B^-1=A^-1*C*B^-1, E*X*E=A^-1*C*B^-1, X=A^-1*C*B^-1.

Пример 1. Решить матричное уравнение

Решение приводится на доске.

Пример 2. Решить матричное уравнение

Решение приводится на доске.

В качестве примера использования элементов теории матриц в экономическом анализе рассмотрим модель межотраслевого баланса В. Леонтьева, которая в западной экономической литературе называется моделью “затраты – выпуск” (Курс экономической теории. Под общей редакцией проф. Чепурина М.Н. 2005). Здесь не приводится полный экономический анализа. Целью этого примера является только иллюстрация использования математических методов в экономических исследованиях.

Схема межотраслевого баланса производства и распределения продукции представляет собой таблицу.

Таблица 1.

	Отрасли–потребители
Отрасли–производители	11	2 2	3 …		n n	Конечный продукт	Валовая продукция
1	Х		…
2			Х
	
n	Х	Х	Х		Х
Добавленная стоимость	W	W	W …		W
Валовая продукция	Х	Х	Х…		Х

В этой таблице показатель Х_ij (i = 1, 2) обозначает стоимость продукции, произведенной в i-й отрасли и потребленной в качестве материальных затрат производства в j-й отрасли. Сумма

представляет собой стоимость промежуточного продукта i-й отрасли, т. е. той части всего продукта отрасли, которая использована в производстве всеми включёнными в баланс отраслями.

Показатель У_i обозначает стоимость конечного продукта i-й отрасли, то есть части всего продукта i-й отрасли, которая идёт на потребление населения, накопление, государственные закупки и другие, не связанные с производством нужды.

Вся экономика, таким образом, в данной модели условно разбивается на два сектора: производящий и потребляющий. Производящий сектор, в свою очередь, разбивается на несколько отраслей, каждая из которых производит однородный продукт.

Показатель Х_i (i =1, 2, ,n) определяется равенством

(1)

и представляет собой стоимость валового продукта i-й отрасли. Из этого равенства видно, что строка таблицы межотраслевого баланса показывает, как распределяется продукт, произведенный отраслью.

В столбце с номером j таблицы отражаются затраты на создание продукта в j-й отрасли. Сумма есть стоимость всех материальных издержек на производство продукта. Если её сложить с величиной добавленной стоимости (заработная плата, прибыль налоги), то в результате получится стоимость валового продукта, произведенного j-й отраслью:

Если в Таблице 1 каждую величину Х_ij поделить на Х_j, то из первых n строк и первых n столбцов получится квадратная матрица А коэффициентов прямых материальных затрат:

A=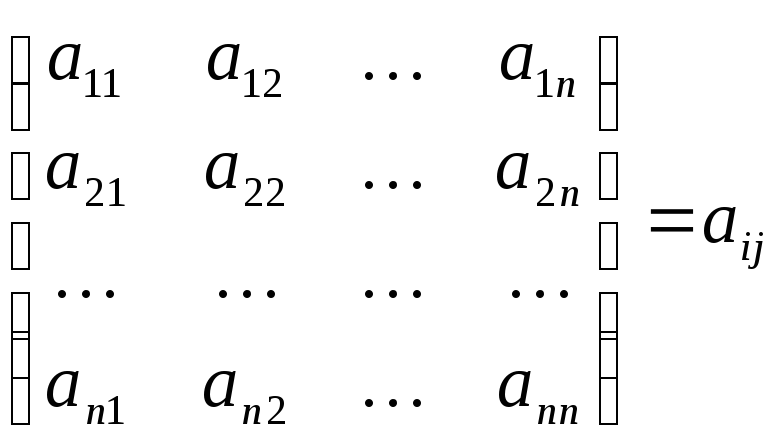 (2)

(3)

Коэффициент прямых затрат показывает, сколько единиц продукции i-й отрасли непосредственно затрачивается в качестве предметов труда на выпуск единицы продукции j-й отрасли. Так, если индексом i обозначена электроэнергетическая отрасль, а индексом j – угольная промышленность, то а_ij – коэффициент прямых затрат электроэнергии на единицу продукции угольной промышленности. При i = j получается коэффициент затрат собственной продукции отрасли на единицу её валового выпуска.

Поскольку с помощью коэффициентов прямых затрат измеряются технологические связи между отраслями, коэффициенты прямых затрат иногда называются технологическими коэффициентами, а матрица А – технологической матрицей. Предполагается, что на определенный период технологические коэффициенты известны и остаются постоянными.

Заменяя в каждом из n равенств (1) величины X_ij их выражениями, полученными из формул (3), приходим к системе n линейных уравнений:

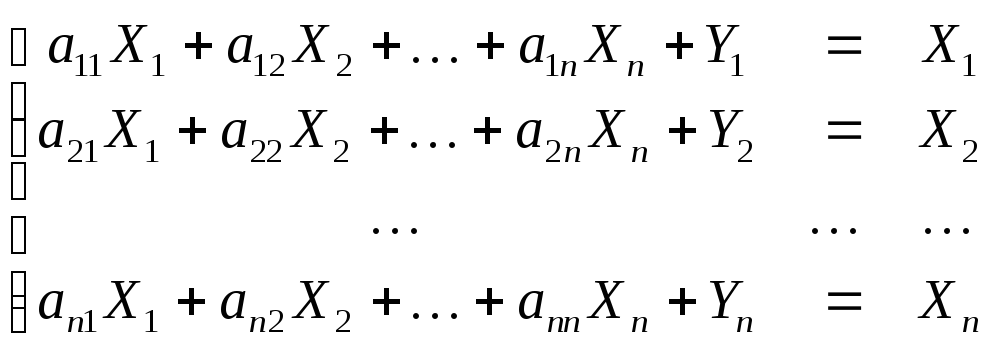. (4)

Эту систему можно представить в матричной форме:

AX+Y=X. (5)

Здесь – вектор валовых выпусков, – вектор конечной продукции.

Система (5) содержит 2n неизвестных – валовые выпуски всех отраслей и величины конечной продукции этих отраслей.

Можно поставить и решить экономическую задачу следующего содержания. Пусть заданы плановые величины конечной продукции всех отраслей. Требуется определить величины валовой продукции, обусловленные технологической структурой производства (коэффициентами прямых затрат). Для решения этой задачи преобразуем систему (5) к виду:

(E–A)X = Y, (6)

где Е – единичная матрица размера n. К такому виду систему можно привести непосредственно из представления (4).

Решение системы уравнений (6) можно также получить в матричной форме:

X = (E–A)^–1Y

Экономический смысл элементов матрицы (E–A)^–1 будет в дальнейшем раскрыт в курсе “Экономико-математические методы и модели”.

Приведём конкретный пример.

Пример 1. С двух каменных карьеров сырьё поставляется на два перерабатывающих завода, потребности, которых 200 т и 300 т ежедневно. Ежесуточная добыча сырья на первом и втором карьерах 350 т и 150 т соответственно. Затраты на перевозку заданы в таблице:

Завод Карьер	1	2
1	15	20
2	8	25

Минимальные затраты на перевозку равны 7950 ед. стоимости. Найти оптимальный план перевозок.

Пусть — количество сырья в тоннах, поставляемое с i-го карьера на j-й завод, i, j=1,2. Тогда получаем систему:

Решаем методом Гаусса. Находим решение