Методика виконання роботи

1. Установити вагу по рівню 2 з допомогою гвинтів 1 (мал. 2).

2. При закритій вазі – аретир 3 в положенні “Закрито” – зняти пластинку 7 з важеля 6.

3. Пересунути аретир в положення “Відкрито”. Установити стрілку 5 на нуль шкали, обертанням коректора 9 сумістити покажчик 4 з нульовою рисою на шкалі.

4. Пересунути аретир 3 в положення “Закрито”, відкрити кришку та підвісити на крючок пластинку 7.

5. На прозору полицю поставити стаканчик з дистильованою водою та гвинтами підняти полицю до зіткнення пластинки з поверхнею рідини.

6. Аретир 3 пересунути в положення “Відкрито”, а потім повільно пересува­ти важіль 8 до моменту відриву пластинки від поверхні рідини. Відмітити силу відриву Fпо шкалі проти стрілки 5. При зворотному русі важеля 8 визначити вагу пластинки з каплею в момент установлення покажчика 4 на нуль.

7. Перед вимірюваннями з іншою рідиною пластинку 7 висушують фільтрованим папером.

8. Вимірювання провести для води та усіх досліджуваних рідин три-п‘ять разів, знайти середню різницю F_x-P_x та , похибки різниць(F_x-P_x) та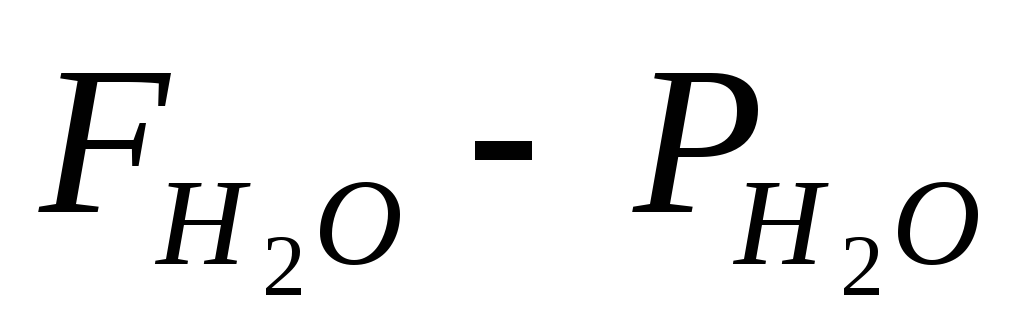(). Результати звести в таблицю.

Вода				Рідина 1				Рідина 2

9. Підрахувати для всіх рідин _x. Похибки_x визначити шляхом диферен­ціювання натурального логарифма функції.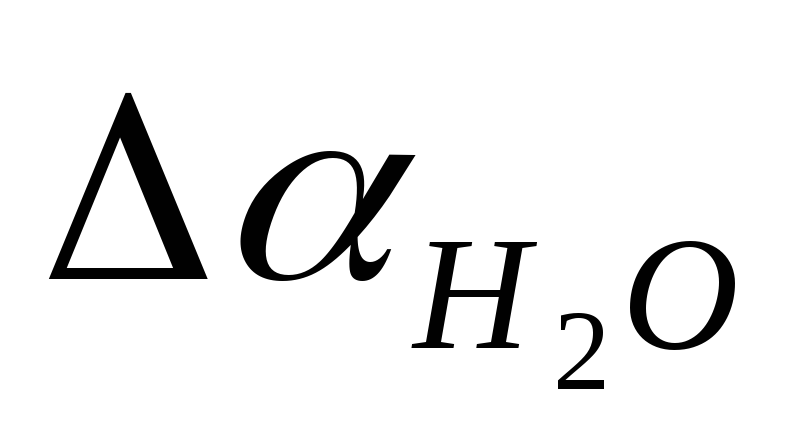знайти за таблицею.

Зауваження.Розчин солі слід добре збовтати перед вимірюваннями ().

Контрольні питання

1. Чим обумовлений поверхневий натяг у рідинах?

2. Енергетичне визначення коефіцієнта поверхневого натягу.

3. Силове визначення коефіцієнта поверхневого натягу.

4. Який вигляд робочої формули?

5. Послідовність операцій при проведенні експерименту.

6. В яку сторону в загальному випадку направлена сила надлишкового тиску під викривленою поверхнею рідини?

7. Умова відриву пластинки від поверхні рідини.

8. Формула сили поверхневого натягу, що діє по периметру пластинки, яка відривається.

9. Яким методом визначається похибка _к?

Література

1. Зисман Г.А., Тодес О.М. Курс общей физики. т.І—М.:Физматгиз, 1972.—с.212-220.

2. Савельев И.В. Курс общей физики. т.І.—М.: Физматгиз, 1977.—с.367-370.

Лабораторна робота м–17 Визначення коефіцієнта в‘язкості по методу Стокса

Мета роботи:вивчення явища в‘язкості (внутрішнього тертя) в рідинах та визначення коефіцієнта внутрішнього тертя рідини по методу Стокса.

Основні поняття явища в‘язкості (внутрішнього тертя) викладені в роботі М‑16.

В‘язкість газів пояснюється переносом кількості впорядкованого руху з одного шару газу в іншу. В‘язкість рідин визначається в основному силами взаємодії між собою (силами зчеплення молекул). В‘язкість газів з підвищенням температури збільшується, так як збільшується швидкість хаотичного руху молекул газу і, отже, перенос кількості руху. З підвищенням температури в‘язкість рідин, навпаки, зменшується та при критичній температурі стає рівною в‘язкості газу.

В методі Стокса при визначенні коефіцієнта внутрішнього тертя розглядаєть­ся рух маленької кульки радіусу R, густина матеріалу якої_т, у в‘язкому середовищі з густиною_ж. На рухому кульку діють:

• сила тяжіння кульки ;

• сила Архімеда ;

• сила внутрішнього тертя рідини (сила Стокса) .

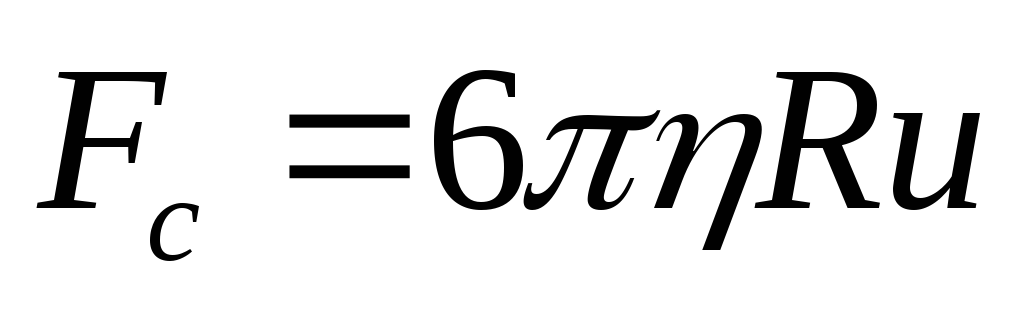Формула Стокса отримана на основі формули Ньютона для внутрішнього тертя.

Коли сила опору стане рівною P-Q, рух кульки буде рівномірним. Отже, в цей момент виконується рівність

,

звідки . (1)

Поблизу поверхонь рідини, стінок та дна посудини характер руху кульки змінюється, тому при виконанні роботи слід враховувати лише ті кульки, які рухаються в середній частині посудини.

Формула Стокса справедлива лише для ламінарного режиму руху рідини, що захоплюється кулькою, т.т. при досить малих значеннях числа Рейнольдса (набагато менше одиниці). Число Рейнольдса в цьому випадку

.

Підставимо в формулу (1) значення швидкості рівномірного руху

,

де l – відстань між візирними нитками;

t – час падіння кульки на цій відстані,

та замінимо радіус кульки її діаметром d:

. (2)