
МИНОБРНАУКИ РОССИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ЧЕЛЯБИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
ФАКУЛЬТЕТ ЗАОЧНОГО И ДИСТАНЦИОННОГО ОБУЧЕНИЯ
КАФЕДРА МАТЕМАТИЧЕСКИХ МЕТОДОВ В ЭКОНОМИКЕ
Контрольная работа
по теории статистики
|
Направление «Экономика»
Дисциплина «Статистика»
Оценка |
Выполнил: Валиуллина В.Н.
Группа: 15 ЭБC - 201
Проверил: Артамонов В.Н. канд. пед. наук, доцент
|
Челябинск
2014
Оглавление
Упражнение 3.1. 4
Вывод: 4
Вывод: 5
Упражнение 3.2. 6
Упражнение 6.1. 10
Упражнение 7.1. 12
Упражнение 7.2. 14
Упражнение 7.3. 17
Список использованной литературы 18
Упражнение 3.1.
По приведенным ниже данным найдите среднюю урожайность всех зерновых культур сельхозпредприятия: а). в отчетном периоде; б). в планируемом периоде. Дайте обоснование соответствующих формул, средних для расчета заданных показателей. Сделайте выводы.
Урожайность сельскохозяйственных культур.
Таблица 3.1
|
Культуры |
Отчетный период |
План на предстоящий период | ||
|
|
Урожайность, ц/га |
Валовой сбор, ц |
Урожайность, ц/га |
Посевная площадь, га |
|
Пшеница озимая |
22,5 |
60 000 |
25 |
3 500 |
|
Кукуруза |
40,2 |
40 000 |
42 |
1 200 |
|
Ячмень яровой |
20,5 |
15 200 |
22 |
4·20 = 80 |
Средняя урожайность в отчетном периоде рассчитывается по формуле
![]() От
=
От
=
![]() =
= =
=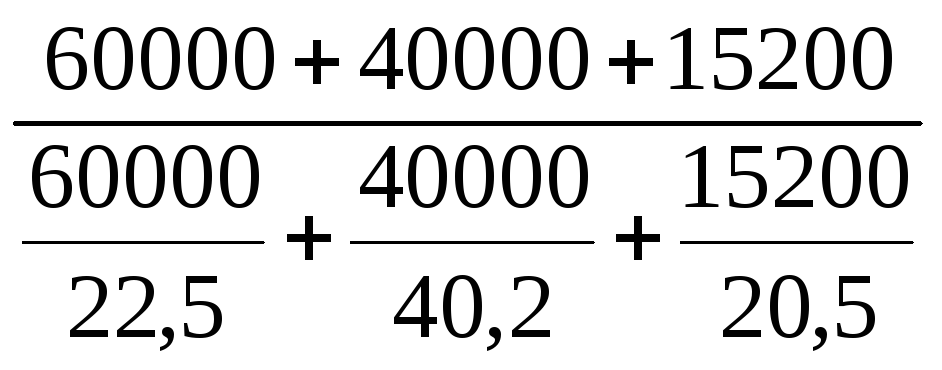 =
=![]()
=
![]() = 26,16 ц/га.
= 26,16 ц/га.
Средняя урожайность в плановом периоде рассчитывается по формуле
![]() Пл
=
Пл
=
![]() =
=![]() =
=![]() =
=![]() =
=![]() = 29,30ц/га.
= 29,30ц/га.
Вывод:
В плановом периоде урожайность должна увеличиться на 29,30–26,16 = 3,14 ц/га
Вывод:
1. Для отчетного периода использовалась средняя гармоническая, а для планового – средняя взвешенная арифметическая. В плановом периоде запланирован рост урожайности на 3,14 ц/га, т.е. на 3,14/26,16*100% = 12%
Упражнение 3.2.
Для изучения производительности труда рабочих завода проведено десятипроцентное выборочное обследование по методу случайного бесповторного отбора, в результате которого получены данные о дневной выработке изделий рабочими.
Таблица 3.2
Дневная выработка рабочих
|
Кол-во изделий за смену, шт. |
Число рабочих |
|
18 |
5 |
|
20 |
10 |
|
22 |
№ = 4 |
|
24 |
45 |
|
26 |
15 |
|
28 |
4 |
|
30 |
1 |
На основании этих данных вычислите:
размах вариации;
среднее арифметическое значение выработки на одного рабочего;
среднее линейное отклонение;
дисперсию;
среднее квадратичное отклонение;
коэффициент вариации;
моду и медиану;
коэффициент асимметрии. Определите, какая асимметрия наблюдается в данном распределении.
Сделайте выводы по указанным пунктам и по всей задаче в целом.
Решение
Пусть Х – количество изделий за смену, шт., f – число рабочих
1) Размах вариации:
R = Хмакс– Хмин = 30–18 = 12
2) Для вычисления среднего арифметического значения выработки на одного рабочего построим таблицу:
|
Xi |
fi |
Xi*fi |
|
18 |
5 |
90 |
|
20 |
10 |
200 |
|
22 |
4 |
22 |
|
24 |
45 |
1080 |
|
26 |
15 |
390 |
|
28 |
4 |
112 |
|
30 |
1 |
30 |
|
Итого |
84 |
1924 |
![]() =
=
![]() = 22,9047
= 22,9047
3) Для вычисления среднего линейного отклонения построим таблицу
|
Xi |
fi |
|Xi–Xср| |
|Xi–Xср|· fi |
|
18 |
5 |
4,9047 |
24,525 |
|
20 |
10 |
2,9047 |
29,050 |
|
22 |
4 |
0,9047 |
3,620 |
|
24 |
45 |
1,0953 |
49,288 |
|
26 |
15 |
3,0953 |
46,429 |
|
28 |
4 |
5,0953 |
20,381 |
|
30 |
1 |
7,0953 |
7,095 |
|
Итого |
84 |
|
180,388 |
![]()
4) Для вычисления дисперсии распределения построим таблицу:
|
Xi |
fi |
Xi–Xср |
(Xi–Xср)2 |
(Xi–Xср)2fi |
|
18 |
5 |
-5,753 |
33,098 |
165,490 |
|
20 |
10 |
-3,753 |
14,086 |
140,857 |
|
22 |
1 |
-1,753 |
3,073 |
3,073 |
|
24 |
45 |
0,2469 |
0,061 |
2,743 |
|
26 |
15 |
2,2469 |
5,049 |
75,729 |
|
28 |
4 |
4,2469 |
18,036 |
72,145 |
|
30 |
1 |
6,2469 |
39,024 |
39,024 |
|
Итого |
81 |
|
|
499,062 |
![]()
5) Среднего квадратическое отклонение:

6) Коэффициент вариации:
![]()
7). Рассчитаем моду. Мода – значение признака, повторяющееся с наибольшей частотой. В нашей выборке имеется такое значение: 24, которое повторяется 45 раз. Мо =24.
8). Медиана – значение Хi , разделяющее выборку на две части, объемы которых меньше половины объема всей выборки.
Номер медианы вычисляется по формуле:
![]() =
=
![]() =41
=41
Накопленные частоты до X1:
F1 = 0, F2 = 5, F3 = 5+10 = 15, F4 = 5+10+1 = 16, F5 = 5+10+1+45 = 61 > 42,
Значит, Ме = X5 = 24.
9)
Коэффициент асимметрии: As
=
![]() =
=
где М3 – центральный момент 3-го порядка. Поострим таблицу:
|
Xi |
fi |
Xi–Xср |
(Xi–Xср)3 |
(Xi–Xср)3fi |
|
18 |
5 |
-5,7108 |
-190,42 |
-952,08 |
|
20 |
10 |
-3,7108 |
-52,86 |
-528,65 |
|
22 |
1 |
-1,7108 |
-5,39 |
-5,39 |
|
24 |
45 |
-0,2892 |
0,02 |
0,68 |
|
26 |
15 |
2,2892 |
11,34 |
170,16 |
|
28 |
4 |
4,2892 |
76,60 |
306,39 |
|
30 |
1 |
6,2892 |
243,78 |
243,78 |
|
Итого |
81 |
|
|
-765,11 |
M3
=
![]()
As
=
![]() =
=
![]() =
=
![]() = –0,618
= –0,618
Так как As < 0, то имеет место левосторонняя асимметрия.
