10. Коефіцієнт кореляції

Якщо певному значенню однієї величини відповідає не одне, а ціла сукупність значень іншої величини, то вважають, що між цими двома величинами існує кореляційний зв'язок. Кореляційний зв'язок наявний тоді, коли явище, що вивчається, піддається впливові не одного, а багатьох різних факторів. Так, стаж впливає на продуктивність праці, але не визначає її повністю, оскільки продуктивність праці залежить також від рівня освіти, віку робітника, його кваліфікації та ін.

Для об’єктивного виміру ступеня щільності лінійної залежності між двома змінними х та у використовується коефіцієнт кореляції Пірсона. Це найпростіший критерій який дає кількісну оцінку зв’язку між двома змінними.

Цей показник завжди набуває значення в числовому інтервалі від -1 до +1. Знак коефіцієнта показує "напрямок" зв'язку. Додатний коефіцієнт кореляції (r > 0) свідчить про "прямий" зв'язок між ознаками (тобто такий, коли збільшення значення однієї ознаки збільшує значення іншої ознаки), а від'ємний (г < 0) — про "зворотний" зв'язок (такий, коли зростання однієї ознаки веде до зменшення іншої ознаки). Так, між заробітною платою робітника та кількістю вироблених ним деталей існує прямий зв'язок (чим більше вироблено деталей, тим вищою буде заробітна плата), а між заробітною платою та кількістю бракованих деталей існує зворотний зв'язок (адже чим більше бракованих деталей було виявлено в продукції певного робітника, тим меншою буде його заробітна плата).

Щільність зв'язку оцінюється за абсолютним значенням коефіцієнта кореляції. Нуль (r = 0) свідчить про відсутність лінійного зв'язку між ознаками. Максимальні значення (r= 1 та r=*-1) коефіцієнта свідчать про строгофункціональний лінійний зв'язок між ознаками (відповідно функціональний прямий зв'язок та функціональний зворотний зв'язок). Проміжні значення (-1 <г<0та0<г<1) інтерпретуються так: чим більшим є абсолютне значення показника, тим тісніший кореляційний зв'язок. Як правило, якщо абсолютне значення коефіцієнта перевищує 0,3, то можна вести мову про помірний лінійний зв'язок між ознаками, а якщо перевищує 0,8 — про дуже тісний зв'язок між ознаками.

Отже, якщо коефіцієнт кореляції Пірсона дорівнює нулю, то не можна говорити про відсутність кореляційного зв'язку між ними; це свідчить лише про відсутність лінійного кореляційного зв'язку.

Його можна розрахувати за формулою:

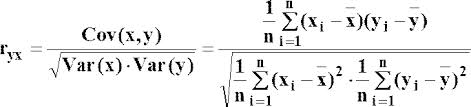
11. Оцінка параметрів лінійної регресії за допомогою метода найменших квадратів

Звернемося до прикладу простої економетричної моделі, де потрібно кількісно оцінити зв’язок між витратами на споживання та доходами сім’ї. Щоб оцінити параметри моделі, необхідно сформувати вихідну сукупність спостережень, кожна одиниця якої характери­зуватиметься витратами на споживання і доходами сімей.

Рис. 2.2. Кореляційне поле точок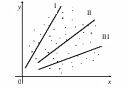

Зобразимо кожну пару спосте­режень у системі координат, де величина витрат на споживання відкладається на осі ординат, а доходів — на осі абцис. У результаті дістанемо кореляційне поле точок (рис. 2.2).

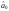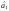На підставі гіпотези про лінійність зв’язку між витратами на споживання і доходом сімей (див. рис.2.2), через кореляційне поле точок можна провести безліч прямих ліній, які різняться між собою параметрами і. Так, якщо витрати на споживання описуватимуться прямою I, то відхилення їх фактичних значень від розрахункових матимуть переважно знак «мінус». Якщо вони описуватимуться прямою III, то ці відхилення будуть переважно додатними, а якщо прямою II, то кількість від’ємних і додатних відхилень буде приблизно однаковою. Наявність серед відхилень переважно від’ємних чи додатних значень підтверджує, що вони мають невипадковий характер. А це означає: певна пряма лінія не адекватно описує фактичну залежність між витратами на споживання і доходом сімей. Звідси постає задача — застосувати метод найменших квадратів для оцінювання параметрів моделі, щоб відхилення фактичних витрат од розрахункових на основі прямої мали приблизно однакову суму від’ємних і додатних значень, а також були б найменшими. Останнє буде свідчити про те, що розрахункові значення витрат на споживання максимально наближені до фактичних, а це є гарантом вірогідності моделі.

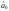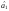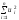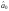Принцип найменших квадратів відхилень полягає в знаходженні таких і, для якихнайменша. Необхідна умова для цього — перетворення на нуль похідних цієї функції за кожним із параметріві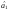. Метод, який реалізує принцип найменших квадратів, називається методом найменших квадратів. Оскільки

,

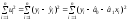то

Виконавши елементарні перетворення, дістанемо систему нормальних рівнянь

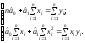(2.19)

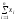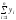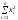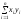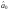Підставимо в систему (2.19) значення ,,,, які можна дістати на підставі сукупності спостережень, і розв’яжемо її відносно невідомих параметріві: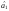

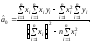
Оскільки оцінки найменших квадратів такі, що лінія регресії обов’яз­ково проходить через точку середніх значень (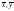), то оцінки параметрів моделі можна знайти дещо інакше.

Поділивши перше рівняння системи (2.19) на n, дістанемо:

.

.

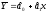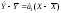Нехай 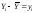,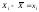і, тоді

,

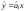а відхилення фактичних значень від теоретичних будуть такі:

.

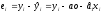Ця різниця називається помилкою, відхиленням або залишком. Можна визначити величину цих помилок для всіх точок спостереження.

Сума квадратів залишків при цьому

.

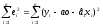Мінімізація цієї суми за невідомим параметром 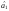дає співвідношення:

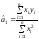. (2.21)

Крім того, можна помітити, що 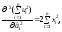тобто друга похідна за параметром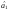від суми квадратів відхилень додатна. Отже, знайдене значеннявідповідає мінімуму суми квадратів відхилень.

Параметр 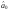можна обчислити:

.
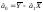