
Контрольная работа 1 АПз-310 / Электроника Ч2
.pdf171
0010 0101 1000.
Формирование цифровой информации может быть различным. В ЭВМ информация вводится в виде цифр. В измерительных приборах измеряемая величина преобразуется, например, в уровень напряжения, который затем преобразуется в код, определяющий результат измерения числом. В систе- мах связи непрерывный сигнал дискретизируется по времени, каждый дис- кретный отсчет квантуется по уровню, а затем уровень каждого дискретного отсчета преобразуется в код. Такое преобразование выполняется аналого- цифровыми преобразователями.
2. ОСНОВНЫЕ ОПЕРАЦИИ И ЭЛЕМЕНТЫ АЛГЕБРЫ ЛОГИКИ
Основой построения любого устройства, использующего цифровую информацию, являются элементы двух типов: логические и запоминающие. Логические элементы выполняют простейшие логические операции над цифровыми сигналами. Запоминающие элементы служат для хранения циф- ровой информации (состояния разрядов кодовой комбинации).
Логическая операция состоит в преобразовании по определенным пра- вилам входных цифровых сигналов в выходные. Математически цифровые сигналы обозначают поразрядно символами, например, x1, x2, x3, x4. Их на- зывают переменными. Каждая переменная может принимать значение "0" или "1". Результат логической операции часто обозначают F или Q. Он так- же может иметь значение "0" или "1". Математическим аппаратом логики является алгебра Буля. В булевой алгебре над переменными "0" или "1" мо- гут выполняться три основных действия: логическое сложение, логическое
умножение и логическое отрицание.

172
Логическое сложение (дизъюнкция или операция ИЛИ) записывается в виде
F = x1 + x2 + ... + xn .
Правила выполнения операции ИЛИ заключаются в следующем:
0 + 0 = 0; |
1 + 0 = 1; |
|
(29.1) |
0 + 1 = 1; |
1 + 1 = 1. |
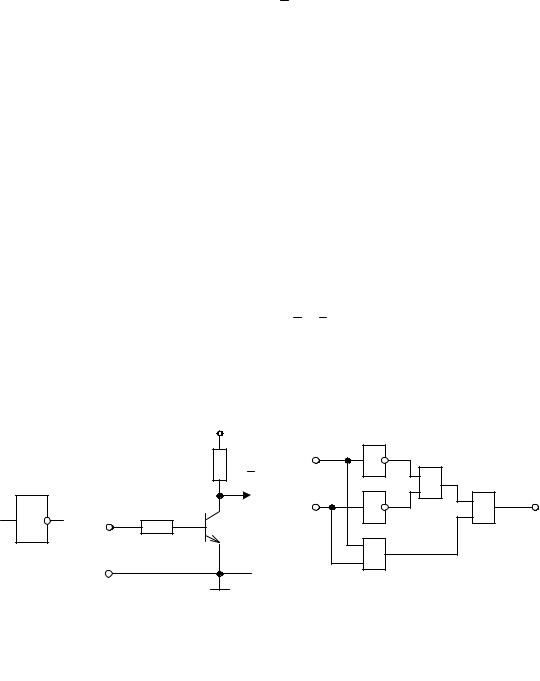
Логические схемы, реализующие операцию ИЛИ, называют ячейками ИЛИ. Их схемное обозначение приведено на рис. 29.1, а. Простейшая реали- зация логической ячейки ИЛИ на диодах приведена на рис. 29.1, б. Напря- жение на выходе схемы будет равно E (F=1), если хотя бы на один из вхо- дов будет подан единичный сигнал.
Логическое умножение (конъюнкция или операция И) записывается в
виде
|
F = x1 x2 ... xn . |
Правила выполнения операции И заключаются в следующем: |
|
0 · 0 = 0; |
1 · 0 = 0; |
|
(29.2) |
0 · 1 = 0; |
1 · 1 = 1. |
Логические схемы, реализующие правила (29.2), называются ячейками И. Их схемное обозначение приведено на рис. 29.1, в. Простейшая реализа-
ция логической ячейки И на диодах приведена на рис. 29.1, г.
173
Напряжение на выходе Uвых ≈ E (F = 1) только в том случае, если все диоды будут закрыты, т. е. на всех входах будет потенциал Е (логическая 1). В противном случае открывшийся диод шунтирует нагрузку и Uвых ≈ 0 .
Логическое отрицание (инверсия или операция НЕ) записывается в виде
F = x
и читается: F равно не x. Правила выполнения операции НЕ заключаются в следующем:
|
|
|
|
|
|
0 = 1; |
0 = 0; |
||||
|
|
|
|
(29.3) |
|
1 = 0; |
|
|
|||
1 = 1. |
|||||
Логические схемы, реализующие правило (29.3), называются ячейками НЕ. Их графическое обозначение приведено на рис. 29.2, а. Операция НЕ может быть реализована схемой транзисторного ключа (рис. 29.2, б).
Рассмотренные логические правила и схемы позволяют реализовать сколь угодно сложную логическую функцию. Например, функция
F = x1 x2 + x1 x2
реализуется пятью логическими элементами, в том числе два элемента И, два элемента НЕ и один элемент ИЛИ (рис. 29.2, в).
Все логические элементы выпускаются в микросхемном исполнении.

174
Они входят в состав всех серий цифровых микросхем и имеют следующие
условные обозначения: |
|
|
|
- |
элементы "ИЛИ" – ЛЛ; |
|
|
- |
элементы "И" |
– ЛИ; |
|
- |
элементы "НЕ" |
– ЛН. |
|
Например, микросхема К555 ЛИ1 |
имеет в своем составе 4 элемента |
||
"И" на два входа каждый. |
|
|
|
3.ОСНОВНЫЕ ТЕОРЕМЫ АЛГЕБРЫ ЛОГИКИ
Теоремы для одной переменной охватывают все операции над пере- менной x и константами "0" и "1":
1. |
x + 0 = x; |
5. x 0 = 0; |
9. x = x. |
|||||
2. |
x + 1 = 1; |
6. x 1 = x; |
|
|||||
3. |
x + x + ... + x = x; |
7. |
x x ... x = x; |
|
||||
|
|
|
|
|
|
|
|
|
4. |
x + x = 1; |
8. |
x x = 0; |
|
||||
Порядок выполнения операций над двумя и более переменными – x и y определяется следующими законами:
1.Переместительный закон:
x + y = y + x; |
x y = y x. |
2.Сочетательный закон:
x + y + z = x + ( y + z) = (x + y) + z; x y z = x ( y z) = (x y) z.
3.Распределительный закон:
x( y + z) = xy + xz;
x + y z = (x + y) (x + z).
Доказательство закона:

175
(x + y)(x + z) = x x + x y + x z + y z = x + x y + x z + y z =
x(1 + y + z) + y z = x 1 + y z = x + y z.
Здесь к скобке применена теорема 2.
4.Закон поглощения:
x + xy = x, x( x + y) = x.
Доказательство закона:
x + xy = x(1 + x) = x 1 = x.
5.Закон поглощения при инверсии одной из переменных:
(x + y) y = xy; x y + y = x + y.
Доказательство закона:
(x + y)( y + y) = xy + yy + x y + y y = x y + xy + y =
=x y + y(x + 1) = x y + y.
6.Закон склеивания:
xy + xy = y,
( x + y)( x + y) = y.
Доказательство:
(x + y)(x + y) = xx + xy + xy + yy = y(x + x) + y = y + y = y.
7.Закон отрицания (теорема де-Моргана):
x + y = x y; |
x + y = x y; |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
x y = x + y; |
|
|
|
|
|
|||||
x y = x + y. |
||||||||||
4.БУЛЕВЫ ФУНКЦИИ (ФУНКЦИИ ЛОГИКИ)
Результат выполнения логических операций над двоичными перемен- ными называется булевой функцией F. Она может принимать только два

176
значения – "0" или "1". Задать булеву функцию – значит указать ее значение при всех возможных комбинациях переменных (аргументов). Если число переменных равно "n", то число возможных комбинаций равно 2n . Когда значение функции известно для всех комбинаций, она называется полно-
стью определенной. В противном случае – частично определенной.
Булевы функции необходимы для синтеза цифровых устройств, со- держащих только логические элементы. Для представления булевых функ- ций часто применяют словесное описание, табличное и алгебраическое представление.
Словесное описание функции должно однозначно определять все слу- чаи, в которых выходные сигналы принимают значение "1" или "0". Напри- мер: Спроектировать устройство с тремя входами x1, x2, x3, на выходе кото- рого сигнал F = 1 в случае, если на любые два или на все три входа подан сигнал "1".
Табличное представление – это перечисление всех возможных комби- наций входных сигналов. Для устройства, заданного приведенным выше
словесным описанием, таблица значений имеет вид: |
|
|||||||
|
|
|
|
|
Таблица 29.1 |
. |
||
|
|
|
|
|
|
|
|
|
|
№ п/п |
x1 |
x2 |
x3 |
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0 |
1 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
0 |
1 |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 |
0 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1 |
0 |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
1 |
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
7 |
1 |
1 |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|

177
Такая таблица называется таблицей истинности.
Алгебраическая форма представления булевых функций используется для минимизации (упрощения формул) и для построения логических схем. Существует две формы алгебраических функций – дизъюнктивная и конъ- юнктивная. Дизъюнктивная нормальная форма представляет собой сумму элементарных произведений аргументов, например,
F (x1, x2 , x3 ) = x1 x2 + x2 x3 + x1 x2 x3.
Если каждое слагаемое содержит все аргументы или их отрицания, то по-
лучаем совершенную дизъюнктивную нормальную форму (СДНФ), например,
F (x1, x2 , x3 ) = x1 x2 x3 + x1x2 x3 + x1x2 x3 + x1 x2 x3.
Совершенная конъюнктивная нормальная форма (СКНФ) представля-
ет собой логическое произведение элементарных логических сумм, причем, каждая сумма содержит все аргументы или их отрицания, например,
F (x1, x2 , x3 ) = (x1 + x2 + x3 ) (x1 + x2 + x3 ) (x1 + x2 + x3 ) .
Для перехода от таблицы истинности к СДНФ учитываются только те состояния, для которых функция равна 1. Для каждого такого состояния за- писывается элементарное произведение всех аргументов. Если аргумент имеет значение "0", то записывается его отрицание. Для приведенного при- мера СДНФ имеет вид
F (x1, x2 , x3 ) = x1x2 x3 + x1 x2 x3 + x1x2 x3 + x1x2 x3. |
(29.4) |
Для перехода от таблицы истинности к СКНФ учитываются только те состояния, для которых функция равна "0". Для каждого такого состояния за- писывается элементарная сумма аргументов. Если аргумент имеет значение "1", то пишется его отрицание. Для приведенного примера СКНФ имеет вид
F(x1 , x2 , x3 ) = (x1 + x2 + x3 ) (x1 + x2 + x3 ) (x1 + x2 + x3 )
(29.5)
(x1 + x2 + x3 ).

178
На основании полученных формул (29.4) или (29.5) можно построить логическую схему, состоящую из элементов "ИЛИ", "И", "НЕ". Для функции (29.4) схема приведена на рис. 29.3, а. При построении схемы сначала изо- бражаются инверторы, затем ячейки "И" и потом ячейки "ИЛИ".
Схемы рис. 29.2, в и рис. 29.3 содержат все типы логических элемен- тов. При проектировании всегда стремятся сократить перечень используе- мых элементов. В связи с этим созданы логические элементы, способные выполнить простейшую функцию двух аргументов "ИЛИ-НЕ", а также "И- НЕ". С помощью каждого из этих элементов можно выразить все основные операции булевой алгебры, а значит, реализовать любую логическую функ- цию. Покажем это.
Для элемента "ИЛИ-НЕ"
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = x + x |
|
|
x + y = x + y |
|
|
x |
|
|
+ y |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для элемента "И-НЕ"
|
|
x = x x |
|
|
|
|
x + y = x y |
|
|
|
|
|
x y = x y |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В микросхемном исполнении элементы "ИЛИ-НЕ" обозначаются ин- дексами ЛЕ, а элементы "И-НЕ" – индексами ЛА. Например, микросхема

179
К555 ЛЕ1 имеет в своем составе четыре элемента "ИЛИ-НЕ" на два входа каждый.
5. МИНИМИЗАЦИЯ БУЛЕВЫХ ФУНКЦИЙ
Булевы функции в СДНФ и в СКНФ обычно избыточны, поэтому эта- пу построения схемы должно предшествовать упрощение формул или ми- нимизация. Цель минимизации – получить минимально необходимое ко- личество логических элементов в схеме. В основу минимизации положе- ны правила и законы булевой алгебры. Чаще других применяется теорема склеивания:
(x y + xy) = x.
Для применения этой теоремы в функции, представленной в СДНФ, отыскиваются слагаемые, отличающиеся только одним аргументом, и склеиваются. Когда все операции склеивания выполнены, можно проверить возможность применения закона поглощения. Для примера проведем мини- мизацию функции (29.4). Добавим в выражение (29.4) еще два слагаемых x1x2 x3 , от этого значение функции не изменится (правило 3). Выражение
(29.4) принимает вид:
F = x1x2 x3 + x1 x2 x3 + x1x2 x3 + x1x2 x3 + x1x2 x3 + x1x2 x3.
Проведем группирование и возможные склеивания: |
|
||||||
|
|
|
|
|
|
|
|
F = (x1x2 x3 + x1x2 x3 ) + (x1 x2 x3 + x1x2 x3 ) + (x1x2 x3 |
+ x1x2 x3 ) = |
||||||
= x2 x3 + x1x3 + x1x2 . |
(17.6) |
||||||
|
|||||||
Вместо четырех слагаемых третьего ранга в (29.4) получили три сла- гаемых второго ранга в выражении (29.6). Схема, соответствующая (29.6)

180
приведена на рис. 29.3,б. Количество логических элементов уменьшилось в два раза. В этом и заключается суть минимизации.
Минимизация булевых функций посредством правил и законов алгеб- ры логики трудоемко, требует хорошей теоретической подготовки и практи- ческих навыков. В инженерной практике для минимизации логических функций, как правило, применяют карты (матрицы) Карно.
Карта Карно представляет прямоугольник, разбитый на квадраты.
Число квадратов равно числу возможных комбинаций, т. е. N = 2n . Каждый квадрат соответствует определенной комбинации аргументов (рис. 29.4, а). Комбинации соседних квадратов должны отличаться не более чем одним ар- гументом.
Для примера на рис.29.4, а все возможные комбинации функции (29.4) внесены в квадраты карты Карно. При таком заполнении карта оказывается загроможденной и не наглядной.
