МОТС / Часть2 / 25. Механизм обслуживания

25. Механизм обслуживания в СМО

При простейшем потоке распределение требований, поступающих в систему, подчиняются закону распределения Пуассона: вероятность того, что в обслуживающую систему за время t поступит именно k требований:

где- среднее число требований, поступивших на обслуживание в единицу времени.

На практике условия простейшего потока не всегда строго выполняются. Часто имеет место нестационарность процесса (в различные часы дня и различные дни месяца поток требований может меняться, он может быть интенсивнее утром или в последние дни месяца). Существует также наличие последействия, когда количество требований на отпуск товаров в конце месяца зависит от их удовлетворения в начале месяца. Наблюдается и явление неоднородности, когда несколько клиентов одновременно пребывают на склад за материалами. Однако в целом пуассоновский закон распределения с достаточно высоким приближением отра­жает многие процессы массового обслуживания. Почему такое предположение в ряде важных случаев оказывается верным, дает ответ общая теорема А.Я. Хинчина, которая представляет исключительную теоретиче­скую и практическую ценность. Эта теорема имеет место в случае, когда входящий поток можно представить в виде суммы большого числа незави­симых потоков, ни один из которых не является сравнимым по интенсив­ности со всем суммарным потоком. Приведем формулировку этой теоремы.

Теорема (А.Я. Хинчина) Если входящий поток представляет собой сумму большого числа независимых между собой стационарных и ординар­ных потоков, каждый из которых вносит малый вклад в общую сумму, то при одном дополнительном условии аналитического характера (которое обычно выполняется на практике) поток близок к простейшему.

Применение этой теоремы на практике можно продемонстрировать, на следующем примере: поток судов дальнего плавания в данный грузовой порт, связанный со многими портами мира, можно считать близким к простейшему. Это дает нам право считать поток прибытия судов в порт распределенным согласно закону Пуассона.

Кроме того, наличие пуассоновского потока требований можно оп­ределить статистической обработкой данных о поступлении требований на обслуживание. Одним из признаков закона распределения Пуассона является равенство математического ожидания случайной величины и дисперсии этой же величины, т.е.

Одной из важнейших характеристик обслуживающих устройств, кото­рая определяет пропускную способность всей системы, является время обслуживания.

Время обслуживания одного требования ()- случайная величина, которая может изменяться в большом диапазоне. Она зависит от стабиль­ности работы самих обслуживающих устройств, так и от различных пара­метров, поступающих в систему, требований (к примеру, различной гру­зоподъемности транспортных средств, поступающих под погрузку или вы­грузку) .

Случайная величина полностью характеризуется законом распре­деления, который определяется на основе статистических испытаний.

На практике чаще всего принимают гипотезу о показательном законе распределения времени обслуживания.

Показательный закон распределения времени обслуживания имеет место тогда, когда плотность распределения резко убывает с возраста­нием времени t. Например, когда основная масса требований обслужива­ется быстро, а продолжительное обслуживание встречается редко. Нали­чие показательного закона распределения времени обслуживания уста­навливается на основе статистических наблюдений.

При показательном законе распределения времени обслуживания ве­роятность события, что время обслуживания продлиться не более чем t, равна:

где v - интенсивность обслуживания одного требования одним об­служивающим устройством, которая определяется из соотношения:

,

где - среднее время обслуживания одного требования одним об­служивающим устройством.

Следует заметить, что если закон распределения времени обслужи­вания показательный, то при наличии нескольких обслуживающих уст­ройств одинаковой мощности закон распределения времени обслуживания несколькими устройствами будет также показательным:

где n - количество обслуживающих устройств.

Важным параметром СМО является коэффициент загрузки , который определяется как отношение интенсивности поступления требований к интенсивности обслуживания v.

где - коэффициент загрузки; - интенсивность поступления тре­бований в систему; v - интенсивность обслуживания одного требования одним обслуживающим устройством.

Получаем, что

Учитывая, что - интенсивность поступления требований в систему

в единицу времени, произведение показывает количество требова­ний, поступающих в систему обслуживания за среднее время обслужива­ния одного требования одним устройством.

Для СМО с ожиданием количество обслуживаемых устройств n должно быть строго больше коэффициента загрузки (требование установившегося или стационарного режима работы СМО) : .

В противном случае число поступающих требований будет больше суммар­ной производительности всех обслуживающих устройств, и очередь будет неограниченно расти.

Для СМО с отказами и смешанного типа это условие может быть ос­лаблено, для эффективной работы этих типов СМО достаточно потребо­вать, чтобы минимальное количество обслуживаемых устройств n было не меньше коэффициента загрузки : _.

_{Формула Литтла}

Рассмотрим вывод формулы Литтла, связывающей (для предельного, стационарного режима) среднее число заявок L_сист, находящихся в системе массового обслуживания (т. е. обслуживаемых или стоящих в очереди), и среднее время пребывания заявки в системе W_сист.

Рассмотрим любую СМО (одноканальную, многоканальную, марковскую, немарковскую, с неограниченной или с ограниченной очередью) и связанные с нею два потока событий: поток заявок, прибывающих в СМО, и поток заявок, покидающих СМО. Если в системе установился предельный, стационарный режим, то среднее число заявок, прибывающих в СМО за единицу времени, равно среднему числу заявок, покидающих ее, так как оба потока имеют одну в ту же интенсивность .

Обозначим: X(t)—число заявок, прибывших в СМО до момента t, Y(t) — число заявок, покинувших СМО до момента t. И та, и другая функции являются случайными и меняются скачком (увеличиваются на единицу) в моменты приходов заявок (X(t)) и уходов заявок (Y(t)). Для любого момента t их разность Z(t) = X(t) - Y(t) — это число заявок, находящихся в СМО.

Рассмотрим очень большой промежуток времени T и вычислим для него среднее число заявок, находящихся в СМО. Оно будет равно интегралу от функции Z(t) на этом промежутке, деленному на длину интервала T:

(1)

Данный интеграл представляет собой площадь фигуры, заключенной между X(t) и Y(t). Фигура состоит из прямоугольников, каждый из которых имеет высоту, равную единице, и основание, равное времени пребывания в системе соответствующей заявки (первой, второй и т. д.). Обозначим эти времена как t₁, t₂,... Правда, под конец промежутка Т некоторые прямоугольники войдут в эту фигуру не полностью, а частично, но при достаточно большом Т этим можно пренебречь. Таким образом, можно считать, что

, (2)

где сумма распространяется на все заявки, пришедшие за время Т.

Разделим правую и левую часть (2) на длину интервала Т. Получим, с учетом (1):

(3)

Разделим и умножим правую часть (3) на интенсивность :

(4)

Величина T — это среднее число заявок, пришедших за время Т. Если мы разделим сумму всех времен t_i на среднее число заявок, то получим среднее время пребывания заявки в системе W_сист .

Итак,

(5)

Это и есть формула Литтла: для любой СМО, при любом характере потока заявок, при любом распределении времени обслуживания, при любой дисциплине обслуживания среднее время пребывания заявки в системе равно среднему числу заявок в системе, деленному на интенсивность потока заявок.

Точно таким же образом выводится вторая формула Литтла, связывающая среднее время пребывания заявки в очереди W_оч и среднее число заявок в очереди L_оч.

Схема размножения и гибели

Процесс размножения и гибели — это случайный про­цесс со счетным (конечным или бесконечным) множе­ством состояний, протекающий в дискретном или не­прерывном времени. Он состоит в том, что некоторая система в случайные моменты времени переходит из одного состояния в другое, причем переходы между со­стояниями происходят скачком, когда наступают не­которые события. Как правило, эти события бывают двух типов: одно из них условно называют рождением некоторого объекта, а второе — гибелью этого объекта.

С помощью процессов размножения и гибели со­ставляются математические модели управления раз­личными процессами, а также модели многих явлений в биологии, физике и других областях. Так, с помощью этой теории могут быть изучены процессы возникнове­ния случайных мутаций, процессы сохранения и рас­пространения мутационного гена, размножение и от­мирание живых организмов, случайные блуждания частиц, описание радиоактивных превращений, обслу­живание абонентов телефонной станции, организация ремонта работающего оборудования, вырождение и выживание популяций организмов. Термин "схема размножения и гибели" заимствован из биологических задач, где состояние популяции определяется числом живых объектов. Представление о характере возника­ющих задач могут дать следующие примеры.

1. В цепной ядерной реакции при столкновении нейтрона с атомным ядром происходит расщепление ядра. В результате появляются различные частицы, в том числе и случайное число новых нейтронов. Пове­дение потомства нейтронов во времени в зависимости от условий может быть различным: оно может неогра­ниченно возрастать (что ведет к ядерному взрыву), на­ходиться в фиксированных пределах (управляемая ядерная реакция) или быть равным нулю (реакции нет). Таким образом, характер реакции зависит от рож­дений и гибели нейтронов.

2. В морской порт прибывают суда со случайными отклонениями от графика. Их разгрузка-погрузка так­же производится с некоторыми отклонениями от гра­фика. Прибытие судна является рождением объекта, а завершение разгрузочно-погрузочных работ – гибелью объекта. Очевидно, что математическая модель этого процесса позволит рационально распорядиться пло­щадками и оборудованием порта.

3. В техническом устройстве (или системе) в слу­чайные моменты времени появляются отказы, в резуль­тате чего ухудшается или теряется его работоспособ­ность. После появления (рождения) отказа происходят его поиск и устранение (ремонт), в результате чего отказ гибнет. Как рождение, так и гибель отказа происходят в случайный момент времени. На основе математической модели этого процесса организуются ремонтно-восстановительные работы, и обосновывается необходимый резерв оборудования.

Перейдем к формальному описанию процесса размно­жения и гибели в непрерывном времени. Будем пола­гать, что в каждый момент времени может произойти рождение или гибель только одного объекта. Число объектов в системе может быть конечным или беско­нечным. Математическая модель не зависит от приро­ды объектов и их физических свойств.

Процесс (или схема) размножения и гибели опи­сывается графом состояний, приведенным на рис. 1.

Рис. 25.1. Граф состояний схемы размножения и гибели

Число состояний равно m+1. Из каждого состояния w_k, k = 1,2,…, m-1, возможны переходы только в со­седние состояния w_k-1 и w_k+1. Переход w_k → w_k+1 (k = 0, 1, 2, …, m-1) означает рождение некоторого объекта, а переход w_k → w_k-1 (k = 1, 2, …, m) – его ги­бель. Таким образом, индекс k в обозначении w_k пока­зывает число объектов, находящихся в системе.

С помощью математических моделей такого про­цесса находят характеристики, которые позволяют производить его анализ, сравнивать между собой раз­личные процессы, выбирать и конструировать лучшие варианты и даже управлять такими процессами. Мы рассмотрим модель на основе теории марковских про­цессов.

Марковский процесс относится к случайным процес­сам с дискретными состояниями и непрерывным вре­менем, то есть нахождение в состояниях и переходы между ними происходят в непрерывном времени. Пе­реход из состояния w_i в состояние w_j за достаточно ма­лый промежуток времени описывается вероятностью:

,

где – параметр, называемый интенсивностью пере­хода w_i → w_i-1 в непрерывном времени, – беско­нечно малая величина более высокого порядка малости по сравнению с при . Если интенсивности не зависят от времени, то процесс будет однородным, а вероятности будут зависеть только от w_i, w_j и дли­ны и не будут зависеть от положения промежутка на оси времени. Для однородного марковского процес­са время нахождения в каждом состоянии распределе­но по показательному закону.

Будем полагать, что время нахождения в каждом состоянии распределено по показательному закону, а пе­реходы между состояниями описываются постоянными во времени интенсивностями. В этом случае для состав­ления математической модели процесса размножения и гибели может быть применена теория однородных мар­ковских процессов. Мы ограничимся рассмотрением только стационарного (установившегося) режима, ко­торый описывается предельными вероятностями и не­которыми обобщенными характеристиками на основе этих вероятностей. Формулы для предельных вероят­ностей процесса размножения и гибели на базе одно­родных марковских процессов известны:

, , (6)

, ,

где – параметр, равный отношению интенсивности перехода к интенсивности перехода .

Можно сформулировать правило вычисления пре­дельной вероятности состояния w_k (k = 1, 2, …, m): ве­роятность состояния равна произведению парамет­ров для всех переходов левее состояния , умноженному на вероятность крайнего левого состоя­ния . Следует отметить, что при имеет место процесс чистого размножения.

Одно из наиболее разработанных приложений схе­мы размножения и гибели – это ее использование для моделирования систем массового обслуживания.

Механизм обслуживания

Обычно различают три характеристики обслуживания:

1. Пропускная способность системы. Пропускная способность определяется как максимальное число вызовов (требований), которые могут обслуживаться одновременно. Если система имеет один канал обслуживания (такую систему называют одноканальной), то пропускная способность равна единице. Будем предполагать, что в наших задачах один канал системы обслуживает один вызов (требование). Однако на практике встречаются системы, когда один канал обслуживает одновременно несколько вызовов (требований).

2. Доступность системы. Чтобы задать доступность системы нужно указать, когда каналы обслуживания являются доступными, а также определить ограничения, снижающие число вызовов, которые могут обслуживаться одновременно по сравнению с полной пропускной способностью системы. Будем предполагать, что в наших задачах системы полнодоступные, т. е. всегда, как только поступая требование, система при наличии свободного канала немедленно приступает к обслуживанию (случаи отключения или выхода каналов из строя рассматриваться не будут).

3. Длительность обслуживания. Под длительностью обслуживания имеют в виду промежуток времени, затраченный на обслуживание одного вызова одним каналом (прибором). В большинстве систем длительность или время обслуживания Т есть величина случайная с собственным законом распределения:

Из физических соображений ясно, что время обслуживания и может быть отрицательной величиной, т.е. F_T(t) = 0 при t<0.

Закон распределения времени обслуживания определяется из опыта путем статистических методов анализа численных значе­ний времени обслуживания реальных систем. Законы распреде­ления могут быть самого различного вида. Однако как в теоретических, так и в практических приложениях, в особенности, большое распространение получил показательный закон.

При показательном законе функция распределения имеет вид:

(9)

а плотность равна

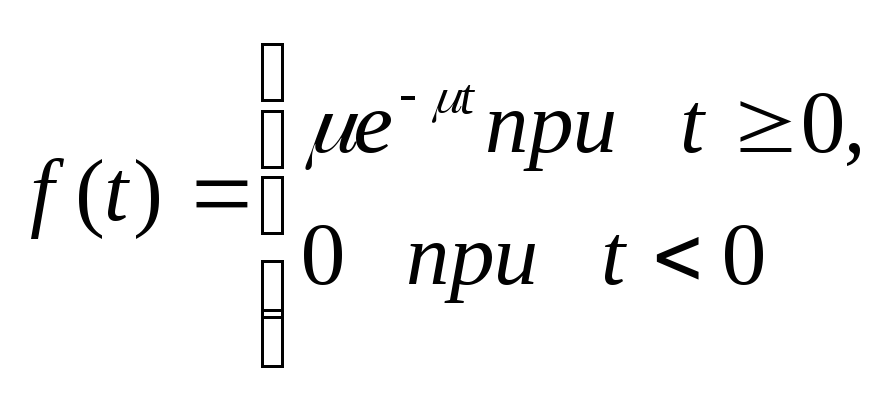(10)

Их графики показаны на рис. 14 и 15.

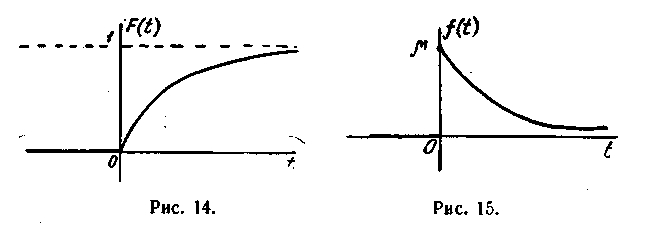
Выясним смысл параметра μ, для чего найдем среднее время обслуживания:

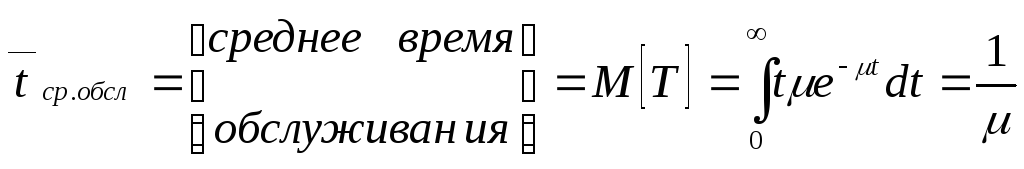(11)

Следовательно, μ=1/t_сробл есть величина, обратная среднему времени обслуживания одного вызова одним каналом, или иначе можно записать:

(12)

Так, например, если за единицу времени принимается один час и если μ=5, т. е. в течение одного часа действующий канал успевает обслуживать пять вызовов, то среднее время обслуживания одного вызова составляет 1/μ=0,2 часа. Аналогично, если

на обслуживание одного вызова в среднем уходит 30 минут, то скорость обслуживания составляет μ=2 вызовам в час (при этом расчет принимается только то время, когда канал занят обслуживанием).

Отметим одно важное свойство показательного закона, распределения времени обслуживания. Предположим, что процесс обслуживания одним каналом некоторого вызова длится t₀, но еще не закончен. Тогда условная вероятность того, что обслуживание закончится в течение интервала h[t₀, t₀+h], будет:

Отсюда можно сделать следующий вывод. Сколько бы не длилось обслуживание вызова, закон распределения оставшейся части времени такой же, как если бы обслуживание только что началось.

Свойство показательного закона распределения длительности обслуживания становится более прозрачным, если воспользоваться разложением e^-μh в степенной ряд:

Таким образом, вероятность завершения обслуживания вызова (освобождение занятого канала) в течение малого промежутка времени h постоянна и совершенно не зависит от того, как долго длилось обслуживание (зависит лишь от длины промежутка h). Здесь налицо отсутствие последействия (отсутствие памяти).

Можно найти следующие вероят­ности, которые будут необходимы при решении задач:

1) Вероятность того, что за время h освободится один (опре­деленный) канал, занятый обслуживанием, совпадает с вероят­ностью того, что обслуживание закончится в течение времени h. Поэтому

2) Вероятность того, что за время h занятый определенный канал не будет освобожден, равна

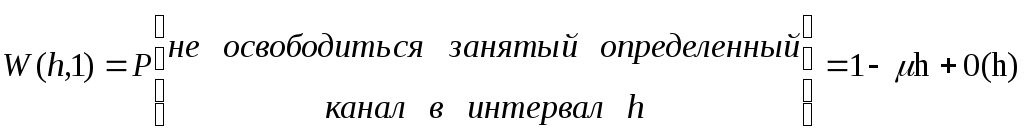
3) Вероятность того, что за время h не освободится ни один из R занятых каналов, равна

Эту вероятность мы определили, используя теорему умножения вероятностей независимых событий (занятые каналы освобож­даются независимо друг от друга).

4) Вероятность того, что за время h освободится хотя бы один из R занятых каналов, равна

Но если учесть, что вероятность одновременного освобождения двух и более каналов за время h имеет порядок о (h), то ве­роятность того, что за время h освободится точно один канал из R занятых, будет равна

В заключение объясним, почему чаще всего предполагают, что время обслуживания подчиняется показательному закону. Прежде всего потому, что показательный закон распределения времени обслуживания хорошо согласуется со статистический данными длительности телефонных разговоров. Однако основной мотив, побудивший принять такое предположение, заключаете в стремлении упростить математическую сторону вопроса.

Показательный закон распределения времени обслуживания допускает, что значительная доля вызовов будет обслуживаться быстро. Однако это не всегда соответствует практике. Поэтому использование показательного закона не всегда законно и применение его во многих задачах осуществляется с большой натяжкой. Правда, при рассмотрении так называемого установившегося (стационарного) состояния системы обслуживания при пуассоновском входящем потоке вид закона распределения времени обслуживания не имеет значения. Следовательно, результаты, полученные для показательного закона распределения, пригодны и для любого другого закона распределения случайной величины T_обсл (теорема Фортье—Севостьянова).