ММО / ММО / Л №2 ММО

2. Методы оптимизации, основанные на классическом математическом анализе.

2.1. Основные понятия теории оптимизации.

Задача поиска наименьшего значения скалярной функции R(x) n-мерного векторного аргумента X = (x₁,x₂,…,x_n)^T при некоторых ограничениях записывается следующим образом:

, (2.1)

Здесь X – подмножество n-мерного евклидова пространства E_n(X∈ E_n) и называется допустимым множеством задачи (2.1), а точки, принадлежащие X – допустимыми точками. Задачу максимизации R(x) можно также представить в форме (2.1), заменив R(x) на (x) = - R(x).

Безусловная минимизация – это решение задачи (2.1) при отсутствии каких-либо ограничений на Х, то есть при X = En.

Задача условной минимизации возникает, когда на переменные x₁,x₂,… ,x_i, x_n наложены ограничения в форме равенств и неравенств:

___

φ_j (x) ≤ 0, j = (2.2)

Здесь X – множество возможных решений системы уравнений (2.2).

Определение 1. Точка доставляет глобальный минимум функции на множестве Х, если

R () ≤ R(X) для  x∈X, ≠X (2.3)

Определение 2. Точка является точкой строгого глобального минимума функции на множестве Х, если

R () < R(X) для  x∈X, ≠X (2.4)

Определение 3. Точка является точкой локального минимума функции R() на множестве Х, если при достаточно малом ε > 0 для  X≠ x∈X,

Удовлетворяющих условию || - X||≤ε, выполнено неравенство:

R () ≤ R(X) (2.5)

Если неравенство (2.5) строгое, то - точка строго локального минимума

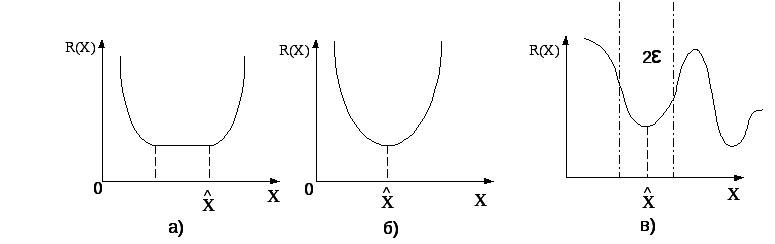
Рис. 2.1. Экстремальный характер функции цели:

1. Глобальный минимум;

2. Строгий глобальный минимум;

3. Локальный минимум.

Класс задач минимизации (максимизации), заведомо имеющих решение, определяется теоремой Вейерштрасса, согласно которой функция R(X) достигает минимума (максимума) на множестве Х, если оно замкнуто и ограничено в пространстве E_n.

Напомним, что множество Х называется ограниченным, если ограничено расстояние между его точками х¹ и х². Расстояние или метрика в евклидовом n-мерном пространстве E_n определяется следующим образом:

где - знак транспонирования

- норма вектора разности между точками х¹ и х² определяется формулой:

.

Множество Х называется замкнутым, если оно содержит внутренние точки, а также все свои граничные точки

Рис.2.1. Внутренняя х¹ и граничная х² точки замкнутого ограниченного пространства.

Сформулировав задачу поиска экстремума, установим необходимые и достаточные условия его существования. При решении данной задачи будем предполагать, что R(X) имеет непрерывные частные производные до второго порядка включительно в окрестностях исследуемой точки.

2.2. Необходимые и достаточные условия существования экстремума одной переменной.

Задача оптимизации ставится следующим образом:

min R(X)

x∈X=E₁

Необходимые условия существования экстремума одной переменной первого порядка.

Теорема Ферма. Для того, чтобы R(x), определённая на вещественной оси E_1, имела безусловный локальный экстремум в т. необходимо:

(2.6)

Доказательство: Пусть точка - точка локального безусловного минимума. Тогда по определению 3 имеем:

R(+ Δx) – R()≥0 , для  Δx = ≤ε . (2.7)

Разложим R() в ряд Тейлора в окрестности точки

R(+ Δx) = R() + Δx ∙ R'() + 0(Δx²) (2.8)

Положим R'() ≠ 0 и выберем Δx = - ρ∙ R'(), где ρ>0.

Тогда из (2.8) получим:

_. (2.9)

Так как lim = 0, ρ≠ 0, то найдётся такое ρ*, что второе слагаемое в правой части выражения (2.9) будет по абсолютной величине меньше первого,

то есть R(+ Δx) – R() < 0, что противоречит условию (2.7).

значит, предположение о том, что R'() ≠ 0 неверно и R'() = 0.

Что и требовалось доказать.

Пример функции одной переменной, определённой на интервале [a,b] представлен на рис.2.2. Применение к данной функции условия (2.6) позволяет выделить ряд точек, в которых оно соблюдается. Это точки, в которых тангенс угла наклона касательной равен нулю (в соответствии с геометрическими смыслом производной).

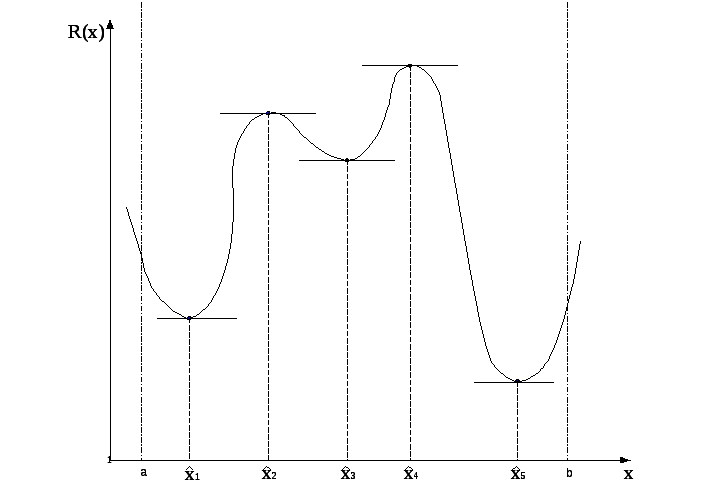
Рис.2.2. Критерий оптимальности со множеством экстремальных точек.

Вместе с тем, если бы мы не имели геометрического изображения исследуемой функции, то не смогли бы ответить на вопрос: в какой точке функция имеет локальный минимум, а в какой максимум?

Следовательно, необходимые условия (2.6) позволяют лишь выявить точки, подозреваемые на экстремум. Эти точки называются стационарными, так как значение функции изменяется справа и слева от них, а в самих точках оно неизменно – стационарно.

Таким образом, условие (2.6) не определяет характера стационарной точки, - оно одинаково как для точек минимума, так и для точек максимума. Для того, чтобы установить характер экстремальной точки, необходимо исследовать производные более высокого порядка.

Достаточные условия существования экстремума одной переменной первого порядка.

Теорема 1. Для того, чтобы R(x), имела в стационарной точке безусловный локальный минимум (максимум) достаточно, чтобы её вторая производная в точке была положительна (отрицательна):

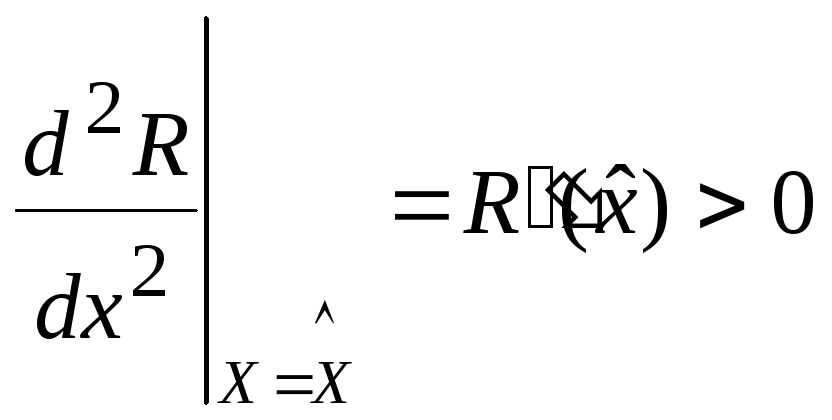(2.10)

Доказательство: Так как точка - стационарная, то разложение в ряд Тейлора в окрестности этой точки с учётом членов второго порядка малости будет:

R(+ Δx) - R() = Δx² ∙ R''() (2.11)

Допустим, теорема не верна, то есть R''()<0. тогда из формулы (2.11) следует:

R(+ Δx) - R()<0,

Что противоречит определению локального безусловного минимума (2.5).

Следовательно, наше предположение о том, что R''()<0 ложно и R''()>0.

Что и требовалось доказать.

Допустим теперь, что R'() = 0 и R'' () = 0. Тогда, полученные нами условия не определяют характера экстремума. Очевидно, надо рассмотреть производные более высокого порядка.

Пусть R(x), определённая на множестве X = E_1, имеет непрерывные производные до k-го порядка включительно, причём в точке имеем:

R'() = R'' () = … = R^k-1() = 0; R^k () ≠ 0.

Тогда, если k – чётное, то R (x) имеет в точке локальный минимум при

R^k () > 0 и локальный максимум при R^k () <0. , если k – нечётное, то R (x) не имеет в точке ни локального минимума, ни локального максимума.

2.3. Необходимые и достаточные условия существования экстремума функции многих переменных.

Необходимые условия существования экстремума функции многих переменных.

Теорема 2. Для того, чтобы в точке функция R(x₁,x₂,…,x_n), имела безусловный локальный экстремум необходимо, чтобы все её частные производные обращались в точке в нуль:

Доказательство: Доказательство данной теоремы проводится элементарно – путём последовательно рассмотрения R(x), как функции только одного переменного при постоянных значениях других аргументов. Условие (2.12) может быть записано в следующих эквивалентных формах:

grad R () = ∇ R () = 0, (2.12*)

то есть в нуль обращается n – мерный вектор градиента с компонентами ∂R/∂x_i, i=1,2,…,n.

Условие (2.12) эквивалентно равенству нулю полного дифференциала функции R(x) в точке :

Как и ранее, точки , являющиеся решениями системы уравнений (2.12), будем называть стационарными.

Достаточные условия существования экстремума функции многих переменных.

Допустим, что решение системы (2.12) найдено. Необходимо определить характер стационарной точки. Разложим функцию R(x) в ряд Тейлора в окрестности точки . Учитывая, что ∇ R () = 0, получим:

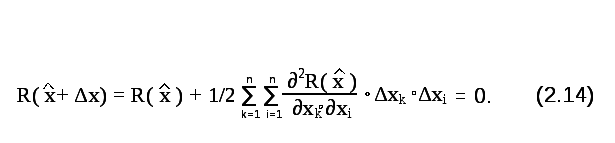
{∂²R/∂x_k•∂x_i } – элементы матрицы Гессе:

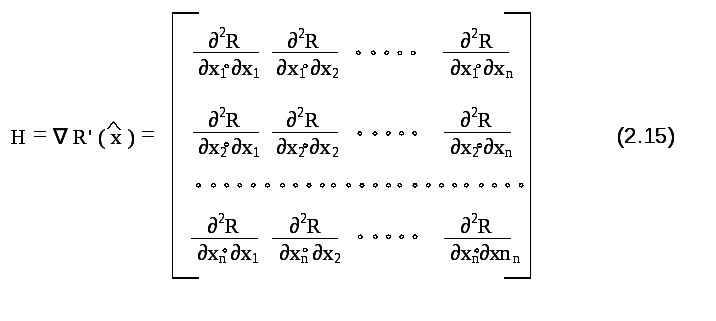
Разложение в ряд Тейлора в векторной форме имеет вид:

R(+ Δx) - R() = Δx^T ∙ H ∙ Δx . (2.16)

Характер стационарной точки определяется знакоопределённостью квадратичной формы, стоящей в правой части выражения (2.16).

Если Δx^T ∙ H ∙ Δx ≥ 0, то квадратичная форма и симметричная матрица вторых производных H неотрицательно определена при любых Δx ≠0,

если Δx^T ∙ H ∙ Δx > 0, то квадратичная форма и симметричная матрица вторых производных H положительно определена при любых Δx ≠0.

Теорема 3. Для того, чтобы дважды непрерывно дифференцируемая функция R(x), имела в точке безусловный локальный минимум (максимум) необходимо, чтобы матрица Гессе была неотрицательно (неположительно) определённой, и достаточно, чтобы она была положительно (отрицательно) определённой.

Доказательство данной теоремы приводится в литературе [Ю.Г. Евтушенко. Методы решения экстремальных задач и их применение в системах автоматизации. М., «Наука», 1982, 432 с.]. В данном курсе мы его не рассматриваем.

Знакоопределённость квадратичной формы выявляется с помощью критерия Сильвестра.

Рассмотрим квадратичную форму: Y^T•A•Y,

где A={a _i,j} - симметричная матрица.

Критерий Сильвестра говорит о том, что необходимым и достаточным условием определённости квадратичной формы является выполнение неравенств:

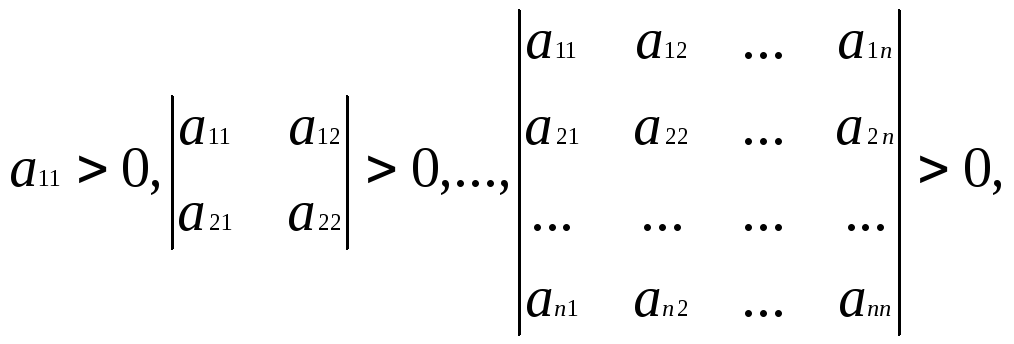(2.17)

то есть все главные определители матрицы A должны быть положительны.

Условия отрицательной определённости состоят в том, что определители нечётного порядка должны быть отрицательны, а чётного – положительны:

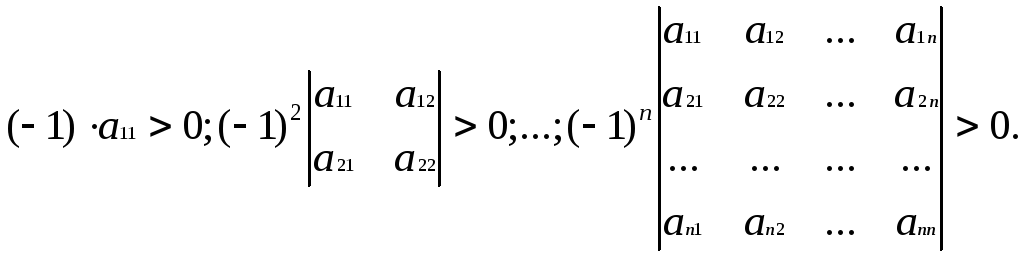(2.17*)

Если последовательность чередования знаков определителей другая, то исследуемая функция не имеет ни минимума, ни максимума.

В том случае, если квадратичная форма не меняет знака, но обращается в нуль при ненулевых значениях аргумента, то для определения характера стационарной точки, исследуют производные высших порядков.