ГОС / 48

48. Статистика Ферми-Дирака. Электронный газ. Уровень и поверхность Ферми. Теплоемкость электронного газа.

Распространим идею Больцмана на газы тождественных микрочастиц, практически не взаимодействующих друг с другом.

Существует два сорта элементарных микрочастиц: ферми – частицы – это частицы с полуцелым спином и бозе-частицы – это частицы с целочисленным спином.

Для ферми – частиц справедлив принцип Паули: в данном квантовом состоянии не может быть двух и более частиц.

Идея Больцмана: каждая частица – это независимая подсистема и к ней применимо распределение Гиббса. Выделим некоторую энергию частиц. В данном квантовом состоянии может быть 0 или 1 ферми-частица. Рассмотрим распределение частиц по числам заполнения данного фиксированного энергетического уровня. Пусть n – число частиц в i – состоянии.

(4.79)

Ω_i - большой потенциал Гиббса для i – состояния (здесь нет суммы по энергетическим уровням).

Для ферми – частиц n=0,1

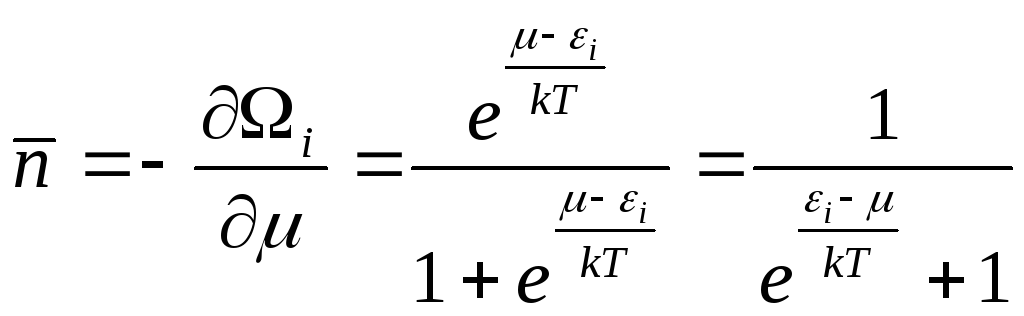(4.80)

- среднее число частиц в k – состоянии с энергией

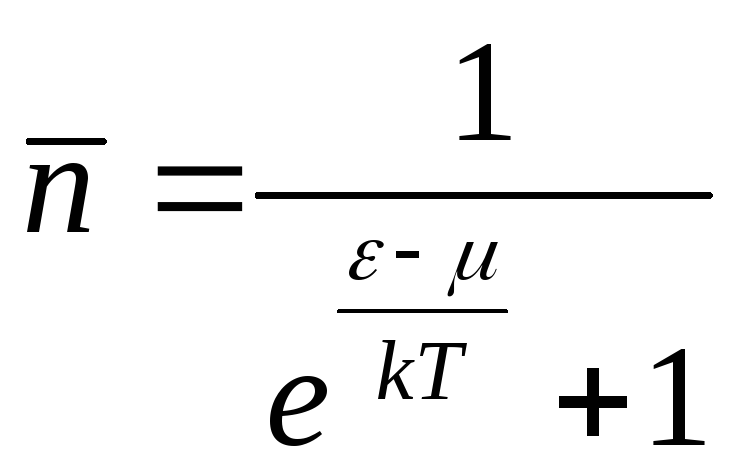- распределение Ферми – Дирака (4.81)

В квазиклассическом рассмотрении: - среднее число частиц в ячейке Больцмана с энергией ε. Условие нормировки

(4.82)

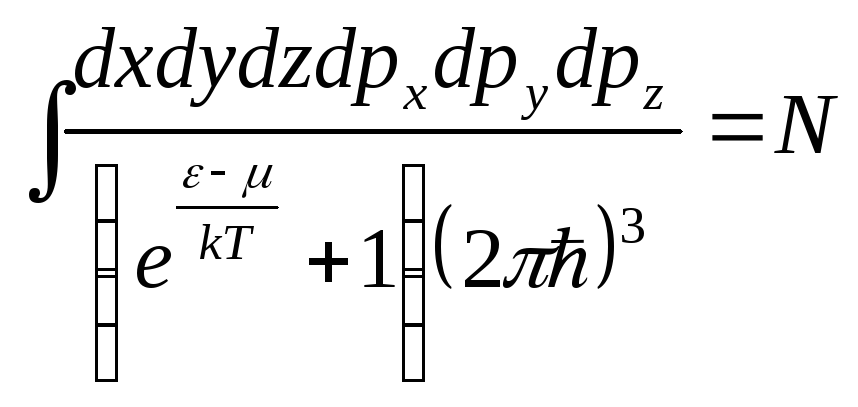
Рассмотрим функцию распределения в пределе низких температур

1 .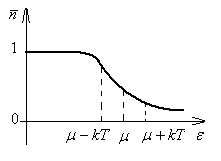

2.

3.

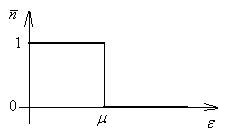
Тот факт, что при низких температурах заполняются уровни начиная с нулевого до значения μ, свидетельствует о «вырождении» газа Ферми.

Обычные больцмановские частицы при все оказались бы на нулевом уровне.

Ферми – газ электронов в металлах является вырожденным при комнатных температурах. Оценки показывают, что kT<<μ при комнатных температурах.

Значения химического потенциала при называется энергией Ферми (верхний из заполненных электронами уровней).

Рассмотрим распределение Ферми в импульсной части фазового пространства.

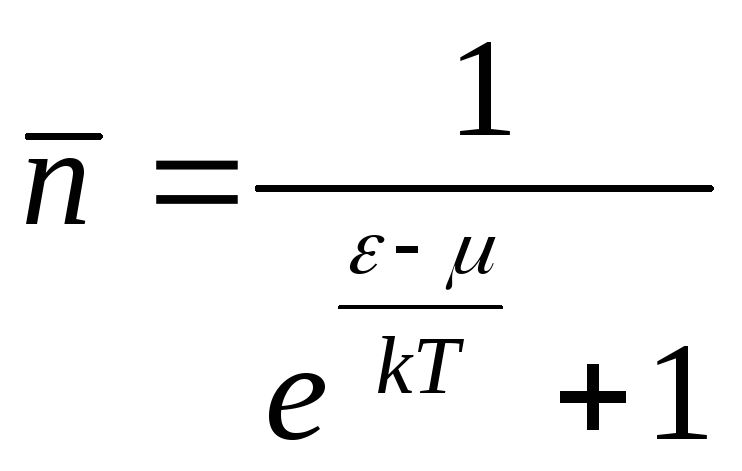
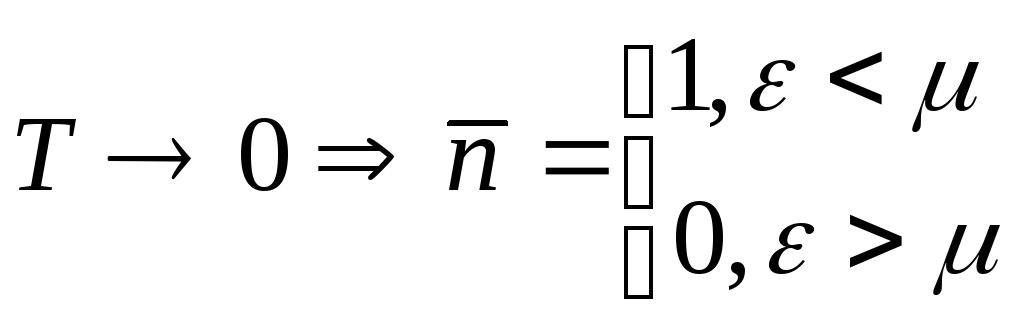
(4.83) – уравнение поверхности Ферми в импульсном пространстве

- уравнение сферы.

При все состояния внутри сферы Ферми заполнены ферми – частицами, вне сферы Ферми – свободны.

Определим положение уровня Ферми при нулевой температуре.

Запишем условие нормировки

- среднее число частиц в ячейках Больцмана, принадлежащих dГ

Для электрона спин равен и в одной ячейке Больцмана может быть две частицы с равной вероятностью.

(4.84)

,

,

Учтем, что

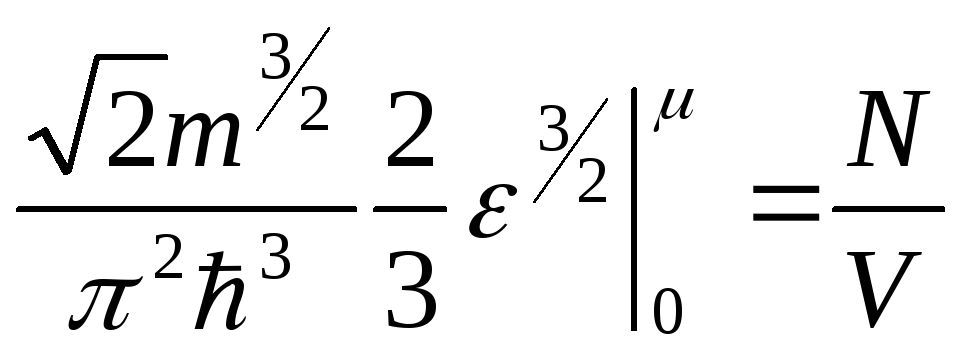
- концентрация электронов, то есть число электронов в единице объёма

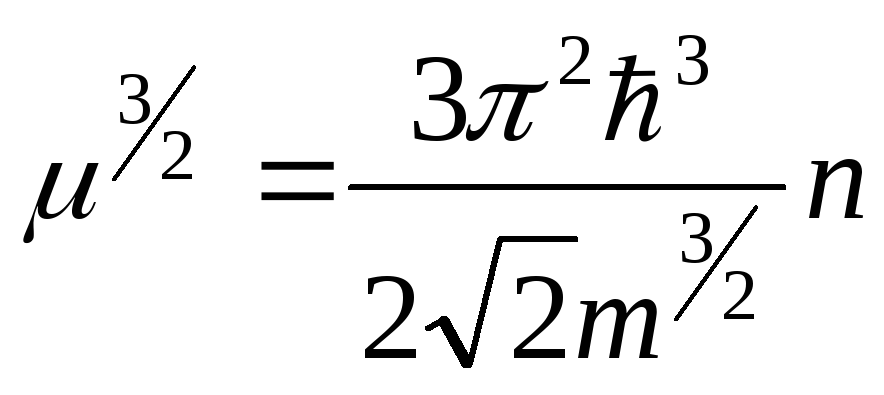
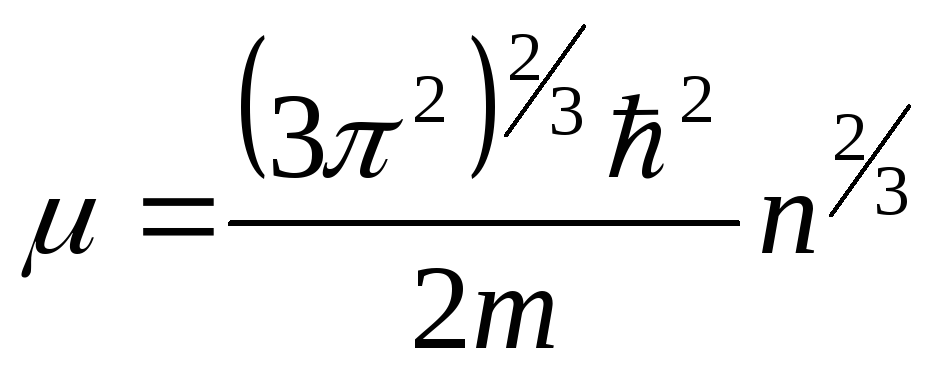(4.85)

Если T~300K kT~0,025 эВ

Если , то частицы заполняют все состояния с энергиями , все вышележащие состояния свободны. Это явление называется вырождением Ферми – газа. В тепловом движении участвуют только частицы вблизи в узком энергетическом слое шириной порядка kT.

В металлах вырождение электронного газа сохраняется вплоть до температуры плавления.

Критерий вырождения.

Газ будет вырожден, если

- условие вырождения (4.86)

При низких температурах число частиц Ферми – газа, участвующих в тепловом движении мало и теплоемкость стремится к нулю

при .

Вычислим среднюю энергию электронного газа

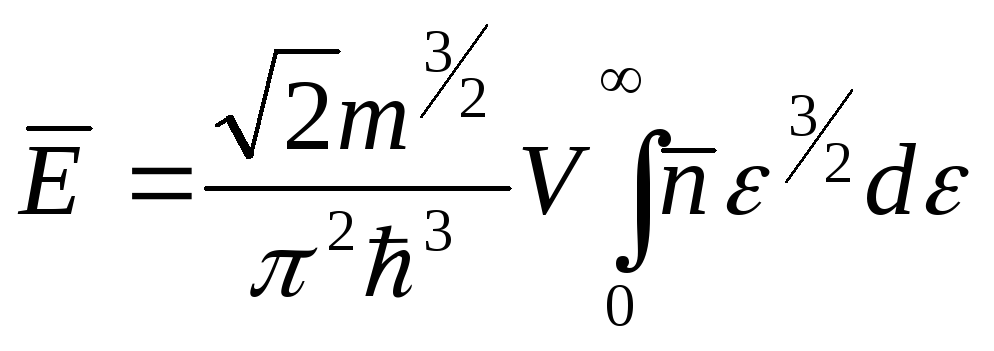(4.87)

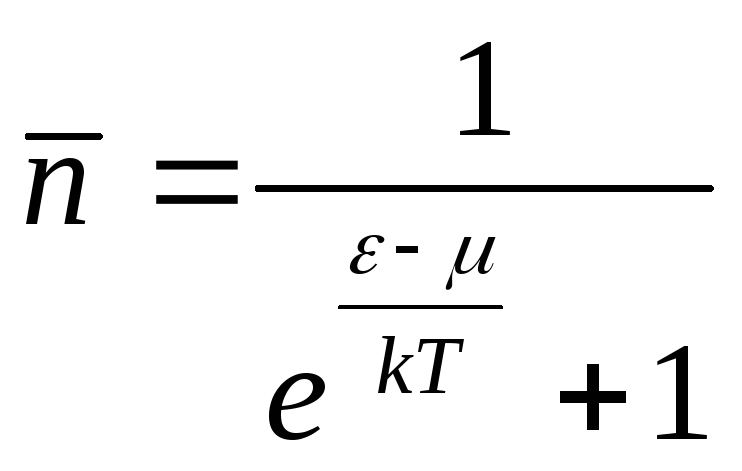(4.88)

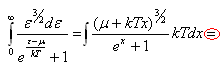
Замена:

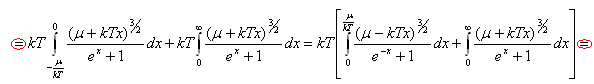
Замена:

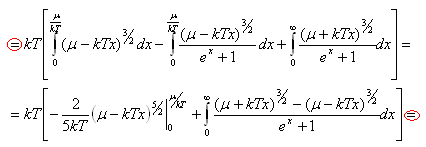
Замена:

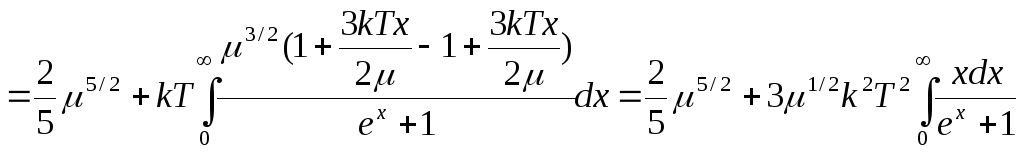
Учитывая значение интеграла , получим выражение для энергии электронного газа

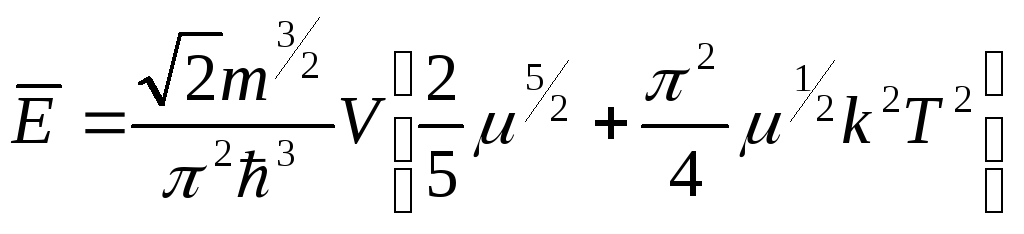(4.89)

Выражение (4.89) справедливо, если

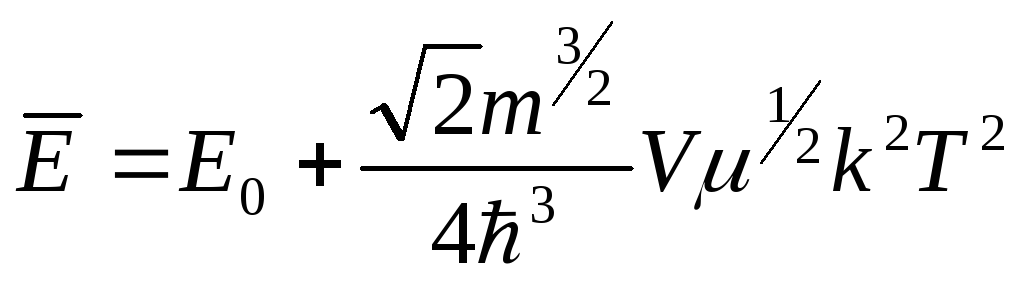(4.90)

Добавка к Е₀ пропорциональна Т² и мала при низких температурах (это и есть энергия теплового движения).

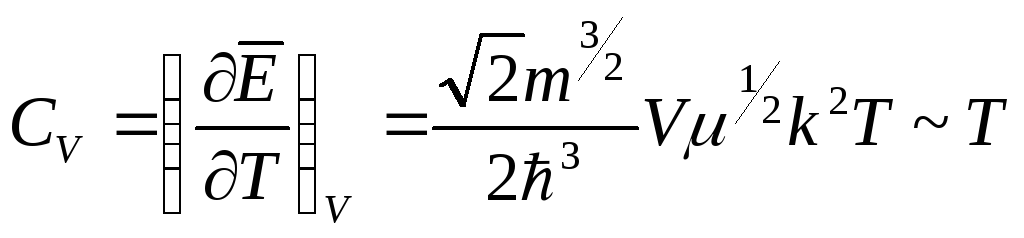(4.91)

Теплоемкость пропорциональна абсолютной температуре, и она мала.

При , что находится в согласии с третьим началом термодинамики.