ГОС / 55

55. Макроскопическая система состоит из N материальных частиц. С позиции классической механики макроскопическая система характеризуется координатами и проекциями импульсов всех частиц, входящих в систему.

Для первой частицы координаты и проекции импульсов , , , , ,

для N-ой частицы , , , , , .

Рассмотрим 6N-мерное фазовое пространство, в котором введена ортогональная система координат, по осям которой откладываются координаты и проекции импульсов всех частиц. Введем обобщенные координаты , , , …, и импульсы частиц , , , …, , характеризующие состояние частиц системы (всего 6N координат и импульсов). Состояние системы изображается точкой в 6N-мерном фазовом пространстве. С течением времени состояние системы изменяется, изображающая точка в фазовом пространстве перемещается в новое положение. В процессе эволюции системы изображающая точка описывает фазовую траекторию в фазовом пространстве , .

p_x

Пример. Осциллятор.

фазовое пространство

имеет 2 измерения (плоскость) x _,

_,

- уравнение эллипса

Пусть dt – малый промежуток наблюдения. Тогда - это вероятность обнаружить систему в определенном макроскопическом состоянии в промежутке времени dt .

Найдем среднее значение : (3.1)

Время наблюдения Т должно быть большим по сравнению с микроскопическими временами ().

- это наблюдаемое значение в эксперименте. Для вычисления среднего необходимо решить микроскопические уравнения движения, а затем выполнить усреднение по времени, что практически невозможно. Поэтому предлагается другой подход, который является основой статистической физики и использует представление о средних значениях физических величин по фазовому пространству. Выделим в фазовом пространстве элемент фазового объема. Вероятность того, что мы обнаружим систему в этом элементе, пропорциональна этому объему.

,

(3.2)

- вероятность обнаружить систему в состоянии изображаемом точкой в элементе объема dГ, w – плотность вероятности, зависящая от места в фазовом пространстве . Если траектории вблизи данного места гуще, то w больше.

(3.3)

это вероятность, приходящаяся на единицу фазового объема.

Рассмотрим некоторую физическую величину f , которая зависит от координат и импульсов частиц .

(3.4)

- фазовое среднее (или среднее в фазовом пространстве, или статистическое среднее).

В реальном физическом эксперименте измеряется среднее по времени наблюдения . Предлагается вычислять фазовое среднее . Возникает вопрос: в каком отношении друг к другу эти средние находятся? Принимается = (это равенство – эргодическая гипотеза).

, .

Гипотеза состоит в предположении, что = , где dt – время суммарного нахождения системы в элементе фазового объема dГ за время наблюдения Т. Это предположение представляется очевидным, если фазовые траектории плотно покрывают фазовое пространство в окрестности рассматриваемой точки. В общем виде, однако, это утверждение не имеет строгого доказательства. Если эргодическая гипотеза верна, то = и определение экспериментальных средних сводится к определению фазовых средних. Вычисление фазовых средних на первый взгляд является еще более сложной задачей, так как вместо интегрирования по времени приходится интегрировать по 6N фазовым переменным. Однако, в большинстве случаев вид функции распределения в фазовом пространстве легко определяется из первых принципов и 6N-кратные интегралы для фазовых средних, сводящиеся к повторным интегралам, вычисляются аналитически.

Рассмотрим статистическую систему, в которой можно выделить отдельные подсистемы. Эти подсистемы малы по сравнению со всей системой, но содержат большое число хаотично движущихся частиц, и сами являются статистическими системами. С точки зрения микроописания:

Первая подсистема характеризуется q⁽¹⁾, p⁽¹⁾ (dГ⁽¹⁾),

вторая подсистема характеризуется q⁽²⁾, p⁽²⁾ (dГ⁽²⁾).

dГ⁽¹⁾ и dГ⁽²⁾ – элементы фазового объема первой и второй подсистемы.

Вся система характеризуется совокупностью координат и импульсов:

q⁽¹⁾, p⁽¹⁾ – первой статистической системы, q⁽²⁾, p⁽²⁾ – второй системы.

dГ = dГ^{(1) .} dГ⁽²⁾ – элементом фазового объема всей статистической системы.

Так как системы являются статистическими, для каждой из них введем функцию распределения.

dW – вероятность обнаружить всю систему в элементе фазового объема dГ.

dW = w (q, p) dГ, где (q, p) (q⁽¹⁾, p⁽¹⁾, q⁽²⁾, p⁽²⁾).

Для первой подсистемы dW⁽¹⁾ = w₁ (q⁽¹⁾, p⁽¹⁾) dГ⁽¹⁾.

Для первой подсистемы dW⁽²⁾ = w₂ (q⁽²⁾, p⁽²⁾) dГ⁽²⁾.

Будем считать, что подсистемы 1 и 2 слабо взаимодействуют друг с другом. Это можно сделать для достаточно больших подсистем, так как взаимодействие происходит в приграничной области, «объем» которой мал по сравнению с общим объемом подсистем.

Считаем, что наступление того или иного события в одной подсистеме не влияет на событие в другой подсистеме, следовательно, dW⁽¹⁾ и dW⁽²⁾ -вероятности независимых событий, значит dW = dW^{(1) .} dW⁽²⁾,

где dW – вероятность сложного события, состоящего в том, что первая подсистема обнаружится в dГ⁽¹⁾, а вторая в dГ⁽²⁾. Тогда

w (q, p) dГ = w₁ (q⁽¹⁾, p⁽¹⁾) dГ^{(1) .} w₂ (q⁽²⁾, p⁽²⁾) dГ⁽²⁾ (3.5)

от сюда

w (q, p) = w₁ (q⁽¹⁾, p⁽¹⁾) ^. w₂ (q⁽²⁾, p⁽²⁾) (3.6)

Если рассмотреть разбиение системы на N подсистем, то функция распределения всей системы w (q, p) = w₁ ^. w₂ ^. … ^. w_N (3.7)

Плотность точек фазового ансамбля с течением времени не меняется. Элемент объема, занимаемый системами ансамбля с течением времени тоже не меняется, так как не меняется число точек в элементе фазового объема (фазовые траектории не обрываются), то есть dГ= dГ’ (теорема Лиувилля).

Функция распределения, на основании теоремы Лиувилля, не меняется со временем и должна выражаться через сохраняющиеся величины. Для системы, состоящей из квазинезависимых подсистем, функция распределения должна мультипликативно выражаться через функции распределения подсистем.

w=w⁽¹⁾w⁽²⁾w⁽³⁾…w⁽ⁱ⁾…w^(N)

тогда ln w=ln w⁽¹⁾+ln w⁽²⁾+ln w⁽³⁾+…+ln w⁽ⁱ⁾+…+ln w^(N) (3.13)

то есть логарифм функции распределения – аддитивная величина. Аддитивными сохраняющимися величинами для замкнутых систем являются полная энергия Е, импульс и момент импульса , следовательно

(3.14)

Выбирая систему координат, так, чтобы полный импульс и момент импульса в этой системе был равен нулю ,, будем иметь (3.15)

Таким образом, логарифм функции распределения линейно выражается через полную энергию системы.

Рассмотрим изолированную статистическую систему. Состояние её изображается точками, лежащими на изоэнергетической поверхности Е(q,p)=E₀.

Пример: для одной частицы , или (3.16)

Это уравнение сферы в импульсном пространстве.

Замечание:

1. Естественно считать, что в любых точках изоэнергетической поверхности статистическая система может появляться с равной вероятностью. Вне точек этой поверхности вероятность обнаружения системы равна нулю.

Т аким образом, функция распределения должна иметь игольчатый характер и быть пропорциональной дельта-функции: (3.17)

Нормированная функция микроканонического распределения имеет вид

(3.20)

-плотность состояний (фазовый объем, приходящийся на единичный интервал энергий). Покажем, как с помощью функции микроканонического распределения можно вычислить среднее значение физической величины f(q,p).

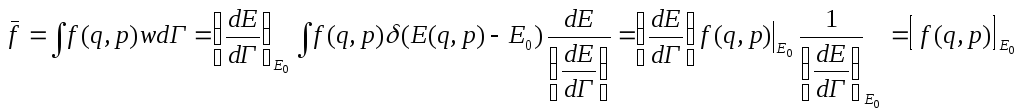Среднее значение физической величины для изолированной системы можно определить, взяв значение этой величины в любой точке изоэнергетической поверхности Е=Е₀.

Р ассмотрим систему, малую по сравнению с термостатом, но являющуюся статистической, то есть содержащей большое число хаотически движущихся частиц.

Система может обмениваться с термостатом энергией. Микросостояние системы изображается точками или ячейками Больцмана. Некоторое же макросостояние описывается совокупностью микросостояний, лежащих в фазовом объёме , соответствующем интервалу энергии .

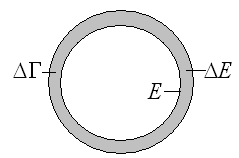- число ячеек Больцмана внутри объёма , то есть число микросостояний, соответствующих некоторому макросостоянию.

Число микросостояний реализующих данное макросостояние называется статистическим весом.

(3.33)

Введем функцию макросостояния – энтропию соотношением

, (3.34) где k- постоянная Больцмана.

Статистический вес для независимых подсистем определяется произведением статистических весов подсистем.

Поэтому энтропия системы определится выражением

(3.35)

Энтропия системы, состоящей из квазинезависимых подсистем, равна сумме энтропий этих подсистем, следовательно, как и энергия, она является аддитивной величиной. Энтропия является функцией состояния, так как определяется числом микросостояний реализующих данное макросостояние. Из определения энтропии следует, что она не является усредненным значением какой – либо физической величины, а имеет статистическую природу. Приведенное рассуждение о статистическом весе, об энтропии возможно для подсистем находящихся в равновесном состоянии, поэтому энтропия является однозначной функцией только равновесных состояний системы.

(3.38) - это каноническое распределение Гиббса.

w_n – вероятность обнаружить рассматриваемую систему в состоянии с энергией Е_n.

Условие нормировки приводит к выражению (3.39)

Введем в рассмотрение статистическую сумму (3.40)

Статистическая сумма z определяется всеми возможными энергетическими состояниями системы при данной температуре. Определим свободную энергию системы (статистически определенная свободная энергия совпадает с характеристической термодинамической функцией F)

(3.41)

(3.42)

Свойства температуры.

Температура является интенсивной величиной, не зависящей от числа частиц системы, и определяемой внутренним характером движения частиц в системе. Рассмотрим две квазинезависимые системы.

Системы 1 и 2 находятся в равновесии порознь и друг с другом.

, поэтому

Должно быть равно , так как подсистемы в равновесии и квазинезависимы.

. Это выполняется если Т₁=Т₂=Т.

Для квазинезависимых подсистем, находящихся в равновесии, температуры должны быть одинаковы. Распределение Гиббса справедливо и для классических систем, когда энергия Е принимает непрерывный ряд значений. В этом случае w – плотность вероятности обнаружить систему в состоянии с энергией Е.