
ГОС / 59
.doc59. Термодинамика устанавливает общие закономерности квазистатических процессов, не вскрывая их молекулярного механизма. При анализе нестатических процессов классическая термодинамика указывает лишь их направление, не давая возможности получать количественные выводы.
Поэтому макроскопическая теория необратимых процессов представляет практический интерес. В большом числе необратимых процессов наблюдается линейная связь между причиной и следствием. Это, например, закон теплопроводности Фурье о пропорциональности теплового потока градиенту температуры (I = - k grad T), закон диффузии о пропорциональности потока массы градиенту концентрации (j = - D grad c), закон Ома о пропорциональности плотности тока градиенту потенциала (j = - γ grad φ), закон Ньютона о пропорциональности силы внутреннего трения градиенту скорости (F = - η grad u).
Если два или больше таких явлений протекают одновременно, то они, налагаясь друг на друга, вызывают появление нового эффекта. Например, от наложения теплопроводности и электропроводности появляется термоэлектричество.
Причины, вызывающие необратимые явления, носят название сил и обозначаются через Yi . Количественные характеристики соответствующих необратимых явлений, вызываемых силами Yi , называются потоками Ii (поток теплоты, диффузии, заряда, импульса).
Все приведенные закономерности получены экспериментально. Наиболее полными и глубокими теориями необратимых процессов являются статистические теории, раскрывающие молекулярно-кинетическую природу этих процессов и позволяющие количественно определить коэффициенты, связывающие силы и потоки (k, D, γ, η).
Обобщение классической термодинамики на неравновесные процессы основывается на понятии локального равновесия. Время релаксации растет с увеличением размеров системы. Поэтому отдельные макроскопически малые части системы приходят сами по себе в равновесное состояние значительно раньше, чем устанавливается равновесие между этими малыми частями. В силу этого, хотя система в целом и не находится в состоянии равновесия, можно говорить о локальном равновесии в макроскопически небольших частях системы, характеризуя их определенными температурой, химическим потенциалом и другими термодинамическими величинами. При этом: 1)малые части должны содержать множество частиц, чтобы эти части можно было считать термодинамическими системами и 2) отклонения от равновесности у данных подсистем должны быть малы.
Точный смысл малости отклонений дает статистическая теория. Для газа в условиях с изменяющейся в пространстве температурой малыми отклонениями от равновесия можно считать такие, при которых изменение температуры на длине свободного пробега молекулы мало по сравнению с самой температурой.
Термодинамика необратимых процессов исходит из основных постулатов:
-
состояние локально равновесных частей системы определяется основным уравнением термодинамики для квазистатических процессов, записанным для единицы объема
![]() (2.111)
(2.111)
Энтропия, как и при равновесии, явно зависит только от термодинамических параметров (U, V, μ) и лишь через них от времени и координат. Локальная скорость возникновения энтропии (производство энтропии) имеет вид
2) поток Ii , вызванный действием сил Yk, пропорционален этим силам
![]() (i
= 1, 2, …, n)
(2.113)
(i
= 1, 2, …, n)
(2.113)
Величины
![]() называются феноменологическими
(кинетическими) коэффициентами.
Диагональные величины определяют
протекание простых явлений, и называются,
например, коэффициентами теплопроводности,
диффузии. Недиагональные ответственны
за налагающиеся явления – например,
термодиффузию и т.д.).
называются феноменологическими
(кинетическими) коэффициентами.
Диагональные величины определяют
протекание простых явлений, и называются,
например, коэффициентами теплопроводности,
диффузии. Недиагональные ответственны
за налагающиеся явления – например,
термодиффузию и т.д.).
3) при соответствующем выборе потоков Ii и сил Yi матрица кинетических коэффициентов является симметричной (соотношения взаимности Онзагера)
![]() =
=
![]() (2.114)
(2.114)
Это означает, что имеется некоторая симметрия во взаимодействии физических процессов. Так, если градиент температуры вызывает поток массы, то градиент концентрации вызовет поток тепла, причем, соответствующие коэффициенты пропорциональности между градиентами и потоками равны.
Приведенные основные положения термодинамики необратимых процессов образуют самосогласованную систему уравнений для определения сопряженных потоков Ii и сил Yi.
Рассмотрим
основные соотношения для случая
стационарной теплопроводности в твердом
теле. Учитываем, что
![]() -
элементарное изменение внутренней
энергии в единице объема вследствие
теплопередачи без совершения
макроскопической работы. Это изменение
в единицу времени определяется количеством
теплоты, втекающим через поверхность
единичного объема в единицу времени,
то есть
-
элементарное изменение внутренней
энергии в единице объема вследствие
теплопередачи без совершения
макроскопической работы. Это изменение
в единицу времени определяется количеством
теплоты, втекающим через поверхность
единичного объема в единицу времени,
то есть
![]() .
Используем уравнение теплопроводности
.
Используем уравнение теплопроводности
![]() .
Тогда
.
Тогда
![]()
Откуда
![]()
Учтем, что плотность
потока тепла, деленная на температуру
есть плотность потока энтропии:
![]() - плотность потока энтропии,
- плотность потока энтропии,
![]() -
термодинамическая сила, соответствующая
этому потоку. Равенство нулю левой части
уравнения соответствовало бы сохранению
энтропии в системе. Отличие от нуля дает
производство энтропии, которое
определяется неотрицательным выражением
-
термодинамическая сила, соответствующая
этому потоку. Равенство нулю левой части
уравнения соответствовало бы сохранению
энтропии в системе. Отличие от нуля дает
производство энтропии, которое
определяется неотрицательным выражением
![]() .
.
Принцип Ле Шателье.
Общие условия устойчивости равновесия термодинамических систем приводят к тому, что внешнее воздействие, выводящее систему из состояния равновесия, вызывает в этой системе такие процессы, которые ослабляют это воздействие. Это положение было установлено Ле Шателье (1884 г) и обосновано Брауном (1887 г). Исторически принцип Ле Шателье был получен в результате поиска термодинамического аналога закона индукции Ленца: индукционный ток имеет такое направление, при котором током создается магнитное поле, препятствующее изменению внешнего поля. Значение принципа Ле Шателье состоит в том, что он позволяет предсказать направление, в котором под влиянием внешнего воздействия изменится термодинамический процесс, протекающий в произвольной системе.
Рассмотрим этот
принцип для систем, в которых сохраняется
химический состав и масса. Пусть состояние
системы определяется параметрами х1
и х2
и
соответствующими им обобщенными силами
Y1
и Y2
. Пусть вследствие изменения Y1
изменяется
x1
. Скорость
изменения х1
определяется производной
![]() .
Однако, важной является роль второго
параметра (и соответствующей обобщенной
силы). Поэтому рассмотрим производную
.
Однако, важной является роль второго
параметра (и соответствующей обобщенной
силы). Поэтому рассмотрим производную
![]()
Но
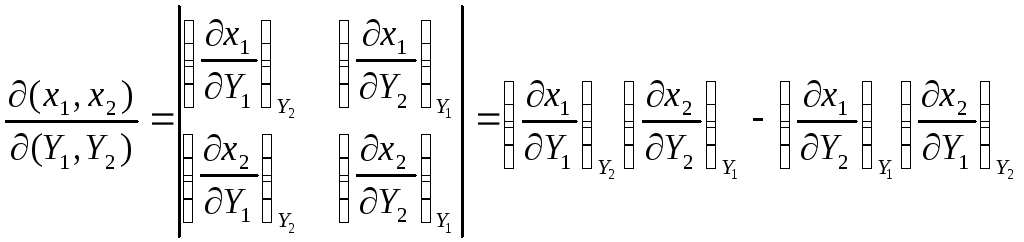
Учтем, что
![]() .
Отсюда
.
Отсюда
![]() .
Поэтому
.
Поэтому
![]()
Условием устойчивости
равновесия является
![]() >
0 . В силу этого
>
0 . В силу этого
![]() (2.115)
(2.115)
Это неравенство
выражает принцип Ле Шателье. Если в
системе, в которой поддерживаются
постоянными параметры х1
и х2
мы начинаем
внешним воздействием Y1
менять
параметр х1
, то это
вызовет изменение х2
и Y2
, а мерой
воздействия является величина
![]() .
При внезапном увеличении Y1
происходящий
процесс можно рассматривать как при
постоянном Y2
. Следовательно,
в это время приложенное воздействие
характеризуется производной
.
При внезапном увеличении Y1
происходящий
процесс можно рассматривать как при
постоянном Y2
. Следовательно,
в это время приложенное воздействие
характеризуется производной
![]() .
Когда же снова наступит равновесие и
параметр х2
примет
поддерживаемое внешней средой прежнее
значение, то изменение величины х1
за счет
внешнего воздействия будет определяться
производной
.
Когда же снова наступит равновесие и
параметр х2
примет
поддерживаемое внешней средой прежнее
значение, то изменение величины х1
за счет
внешнего воздействия будет определяться
производной
![]() .
Принцип Ле Шателье утверждает, что в
новом равновесном состоянии, в которое
переходит система, изменение параметра
х1 за
счет внешнего воздействия ослаблено,
то есть
.
Принцип Ле Шателье утверждает, что в
новом равновесном состоянии, в которое
переходит система, изменение параметра
х1 за
счет внешнего воздействия ослаблено,
то есть
![]()
Ряд примеров подтверждает справедливость принципа Ле Шателье.
-
Термические коэффициенты.
Изменим в некоторый
момент давление на систему. Это вызовет
изменение объема и температуры. Мерой
воздействия будет
![]() ,
так как в силу внезапности изменения
процесс будет адиабатическим. После
установления равновесия и восстановления
прежней температуры величина воздействия
будет определяться производной
,
так как в силу внезапности изменения
процесс будет адиабатическим. После
установления равновесия и восстановления
прежней температуры величина воздействия
будет определяться производной
![]() .
По принципу Ле Шателье будем иметь
.
По принципу Ле Шателье будем иметь
![]() .
.
2. Теплоемкости.
3. Индукционный ток.
