ГОС / 21
.doc21. Энергия магнитостатического поля в вакууме. Магнитный поток. Коэффициенты взаимной и самоиндукции проводников с током.
Запишем выражение для энергии электромагнитного поля в вакууме:
W=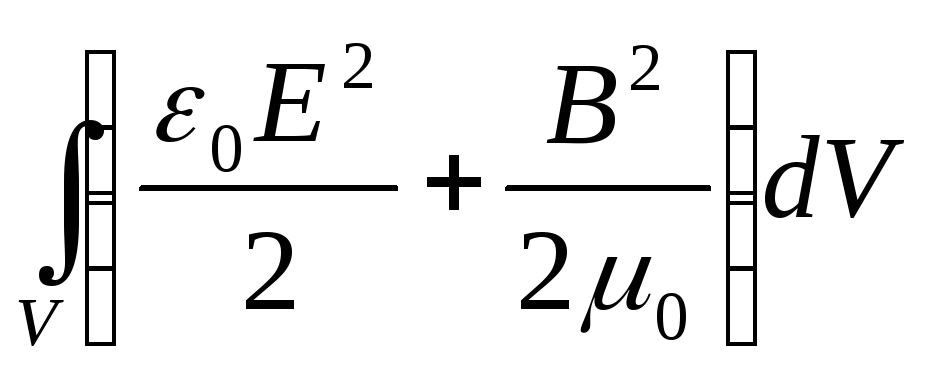 (*)
(*)![]()
WB=![]() (7.1) -
энергия магнитостатического
поля в
вакууме
(7.1) -
энергия магнитостатического
поля в
вакууме
wB=![]() (7.2) - плотность энергии (энергия
магнитостатического поля в
вакууме в единице объема).
(7.2) - плотность энергии (энергия
магнитостатического поля в
вакууме в единице объема).
Выражения (7.1) и (7.2) говорят о том, что энергия магнитостатического поля отлична от нуля в тех областях, где вектор индукции магнитного поля отличен от нуля.
![]()
WB=![]()
![]()
![]()
WB
=![]()
Применим теорему
Гаусса-Остроградского:
![]() (**)
(**)
и третье уравнение
Максвелла:
![]()
WB
=![]()
Рассмотрим все
бесконечное пространство, т.е. V![]() ,
,
![]()
![]()
![]()
![]()
![]()
WB=![]() (7.3)
(7.3)
wB=
![]() (7.4) - плотность энергии
(7.4) - плотность энергии
Выражения (7.3) и
(7.4) говорят о том, что энергия
магнитостатического поля отлична от
нуля всюду, где концентрируются токи,
т.е.
![]() .
.
Выражения (7.1-7.4) выражают одну и ту же величину и для магнитостатического поля используются всегда. Однако (7.1) и (7.2) имеют более широкий физический смысл. Ими можно пользоваться и для переменных магнитных полей, а выражениями (7.3) и (7.4) можно пользоваться только для магнитостатических полей.
Энергия магнитостатического поля отлична от нуля всюду, где есть поле, а не только где есть токи.
Энергия магнитного поля, представляется как энергия взаимодействия элементов с током. Воспользуемся соотношением (7.3):
WB=![]()
![]()
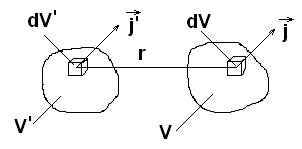
Для того, чтобы вычислить потенциальную энергию взаимодействия токов в объеме V и V’ мы можем воспользоваться функцией (7.3), но при этом интегрирование должно производиться по разным переменным.
WB=![]() (7.5)
(7.5)
WB=![]() (7.5’)
(7.5’)
Энергия магнитного поля для системы линейных токов:
![]()
WB=![]() (7.6)
(7.6)
Энергия магнитного поля с током прямо пропорциональна магнитному потоку и току в этом проводнике.
Рассмотрим систему линейных проводников. Энергия магнитостатического поля i-го проводника:
Wi=![]() (7.6’) `W=
(7.6’) `W=![]() (7.7)
(7.7)
В выражении (7.7) Φi- это полный магнитный поток, пронизывающий площадь, ограниченную i-м контуром, Ii –это ток в i-м проводнике, создаваемый остальными токами.
Коэффициенты взаимной и самоиндукции:
WB=![]() (*)
(*)
Перейдем к линейным проводникам:
![]()
![]()
![]()
WB=![]() (7.8)
(7.8)
Lik=![]()
![]() (7.9)
(7.9)
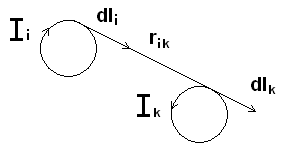
Lik
зависит
только от геометрических размеров и
форм данных проводников, а также от их
взаимного расположения и среды, в которой
они находятся. Не зависит от силы тока,
текущего в каждом проводнике. При этом,
если i=k
, то коэффициенты с индукцией
Lii
называются
коэффициентами самоиндукции. Для одного
проводника этот коэффициент называется
индуктивностью. Если i![]() k,
то Lik
называется
коэффициентами взаимной индукции. С
учетом (7.9) перепишем (7.8)
k,
то Lik
называется
коэффициентами взаимной индукции. С
учетом (7.9) перепишем (7.8)
W=![]() (7.10) – энергия магнитостатического
поля системы линейных проводников.
(7.10) – энергия магнитостатического
поля системы линейных проводников.
Φi=![]() (7.11) – сравнили (7.7) и (7.10)
(7.11) – сравнили (7.7) и (7.10)
Φi можно определить как магнитный поток, определяющийся токами, текущими во всех k проводниках. (7.11) удобно использовать для нахождения взаимной индукции линейных проводников.
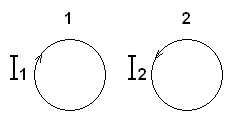
Рассмотрим пример:
i=2
k=1,2
Φ2=I1L21+I2L22
Для того чтобы
найти коэффициенты взаимной индукции
проводников 1,2 удобно положить I2=0
![]() Φ2=I1L21
L21=
Φ2/I1
Φ2=I1L21
L21=
Φ2/I1![]()