ГОС / 05

5. Импульс системы частиц. Изменение импульса. Закон сохранения импульса и его связь с однородностью пространства.

Рассмотрим систему, состоящую из n материальных точек. Обозначим через силу, с которой материальная точка k действует на i -ю материальную точку (т.е. - это внутренняя сила). Обозначим через , результирующую всех внешних сил, действующих на i-тую материальную точку. Тогда, согласно второму закону Ньютона

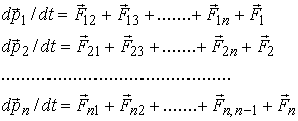(1)

Сложим все эти уравнения

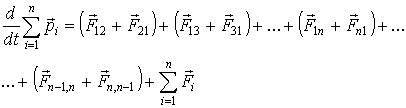(2)

С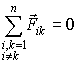огласно третьему закону Ньютона каждая из скобок равна нулю. Следовательно, сумма внутренних сил, действующих на тела системы всегда равна нулю, т.е. . (3)

С учетом этого из (2) получим 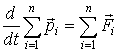. (4)

Введем понятие импульса системы 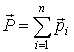. (5)

С учетом этого из (4) находим , (6), где 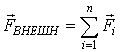, т.е. производная по времени импульса системы равна геометрической сумме внешних сил, действующих на тела системы.

Если , то соответственно и, следовательно, . (7)

Итак, если геометрическая сумма внешних сил, действующих на систему, равна нулю, то импульс системы сохраняется, т.е. не изменяется со временем. В частности, это имеет место, когда система замкнута: .

Импульс замкнутой системы сохраняется.

Это утверждение представляет закон сохранения импульса - фундаментальный закон природы, не знающий никаких исключений. В таком широком понимании закон сохранения импульса не может рассматриваться как следствие законов Ньютона. Оказывается, в основе закона сохранения импульса лежит однородность пространства: т.е. одинаковость свойств пространства во всех его точках.

Можно доказать закон сохранения импульса через однородность пространства.

Однородность пространства означает, что если замкнутую систему перенести на любой вектор в пространстве, то это не повлияет на свойства системы.

Функция Лагранжа L – функция, которая определяет состояние системы в данный момент времени. Она определяется по формуле , где T – кинетическая энергия системы, U – потенциальная. Функция Лагранжа зависит от обобщенных координат, обобщенных скоростей и времени.

Докажем закон сохранения импульса. Выберем обобщенную координату х таким образом, чтобы ее изменение характеризовало параллельный перенос рассматриваемой системы, как целого в данном направлении. Примером такой координаты может служить одна из декартовых координат центра масс. Пространство однородное, поэтому, если система замкнута, то ее смещение в целом вдоль координаты х не влияет на состояние системы, тогда: . Запишем уравнение Лагранжа для координаты х. . Отсюда (1).

Рассмотрим физический смысл этой величины . В классической механике потенциальная энергия от скорости не зависит, поэтому . Отсюда . Поэтому 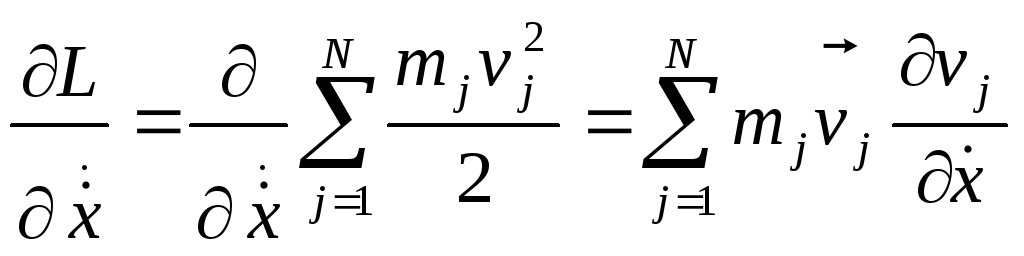(2),

j – номер материальной точки, входящей в систему , - скорость j-ой точки, - ее масса.

Это выражение можно получить, используя правило вычисления производной неявной функции. Вычислим , используя определение производной . Здесь величина переноса всей системы в целом вдоль оси х.

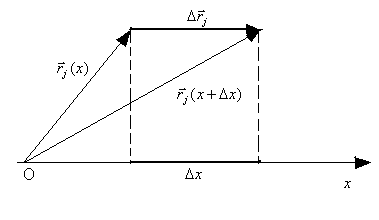
Из рисунка видно, что единичный вектор в направлении х. Поэтому . Подставив полученное выражение в (2) получим 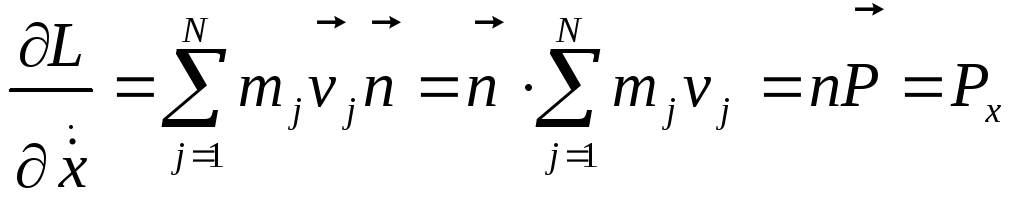. Здесь - вектор общего импульса системы, - его проекция на ось х. Согласно формулы (1) сохраняется в замкнутой системе.

Если при доказательстве в качестве обобщенной выбрать не координату х, а координату у или z, то получим . Поэтому в целом общий импульс системы , что и требовалось доказать.

Так как при доказательстве этого закона пользовались одним постулатом однородности пространства, то закон сохранения импульса является следствием однородности пространства.

3