ГОС / 03

3. Вращение твердого тела относительно неподвижной оси.

Абсолютно твердое тело – это тело деформацией, которого можно пренебречь.

Вращательным называется такое движение, при котором две точки принадлежащие телу остаются все время неподвижными при движении. Прямая проходящая через эти две точки называется осью вращения. При вращении твердого тела вокруг неподвижной оси все его точки описывают окружности, центры которых лежат на оси вращения, а плоскости перпендикулярны к ней. Тело в этом случае обладает одной степенью свободы, поэтому его положение полностью определяется заданием угла поворота из некоторого начального положения.

Угловой скоростью вращения твердого тела называется вектор , численно равный первой производной от угла поворота по времени , и направленный вдоль оси вращения таким образом, чтобы из его конца вращение было видно происходящим против часовой стрелки. Также направление вектора угловой скорости можно определить по правилу буравчика.

Линейная скорость произвольной точки М вращающегося тела определяется по формуле Эйлера , где - радиус-вектор, проведенный в точку М из произвольной точки О оси вращения тела. Численное значение V линейной скорости точки М прямо пропорционально ее расстоянию R от оси вращения.

Вектор направлен по касательной к окружности.

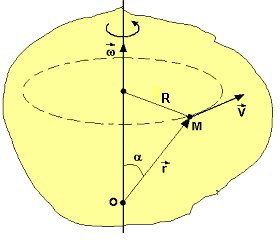
Рис1.

Вращение тела относительно неподвижной оси, проходящей через центр O.

Угловым ускорением вращения твердого тела называется вектор , численно равный модулю второй производной от угла поворота по времени или первой производной от угловой скорости по времени , и направленный в ту же сторону, что и вектор угловой скорости, если движение ускоренной и в противоположную сторону от вектора угловой скорости, если движение замедленное. Если тело вращается равномерно, то

Вектор ускорения каждой точки тела, вращающегося вокруг неподвижной оси, можно разбить на две составляющие: нормальное (центростремительное) и тангенциальное. Вектор нормального ускорения направлен к оси вращения, а по модулю определяется по формуле . Вектор тангенциального ускорения направлен по касательной к окружности, а по модулю определяется по формуле . Отсюда модуль полного ускорения определяется по формуле .

Моментом силы относительно точки О называется векторное произведение радиус-вектора , проведенного из точки О в точку приложения силы на вектор силы , то есть . По модулю момент силы равен произведению модулю силы на плечо (кратчайшее расстояние от центра О до линии, вдоль которой действует сила).

Моментом силы относительно оси называется скалярная величина, равная проекции на данную ось вектора момента силы относительно какой-либо точки той же оси. Разобьем вращающееся тело на малые элементы Δm_i. Расстояния до оси вращения обозначим через R_i, модули линейных скоростей – через V_i. Тогда кинетическую энергию вращающегося тела можно записать в виде:

Физическая величина зависит от распределения масс вращающегося тела относительно оси вращения. Она называется моментом инерции тела относительно данной оси. Для непрерывного тела от суммирования можно перейти к интегрированию. Так момент инерции относительно оси Z определяется по формуле , где - плотность тела.

Например

• Момент инерции стержня относительно оси, которая ему перпендикулярна и проходит через его середину

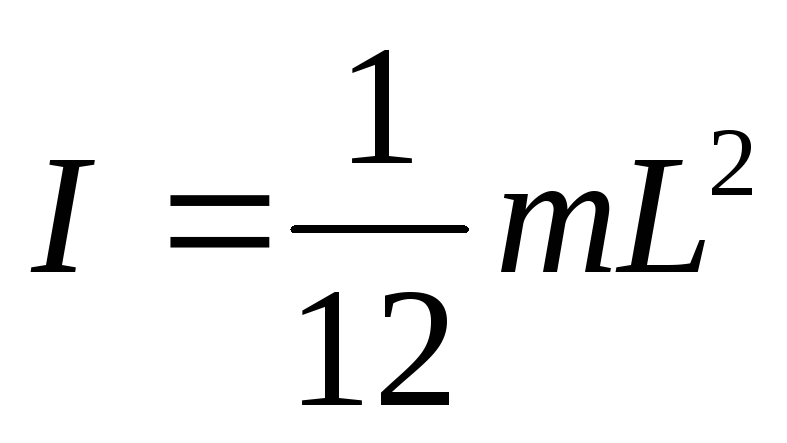
• Момент инерции полого цилиндра относительно его оси

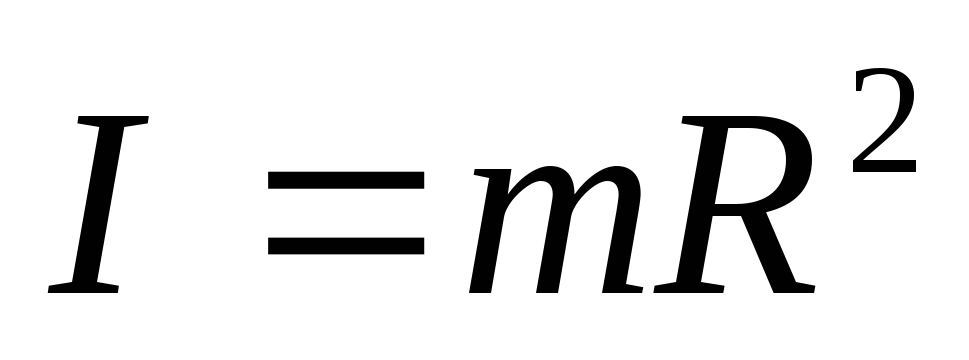
• Момент инерции сплошного цилиндра относительно его оси

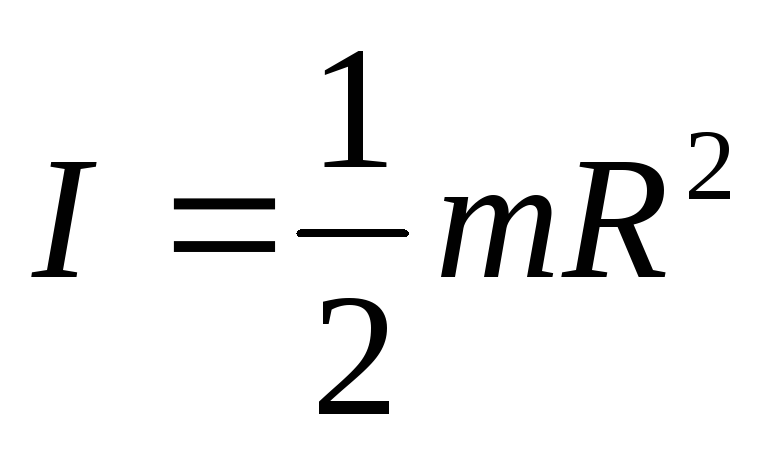
• Момент инерции сплошного шара относительно произвольной оси, проходящей через центр

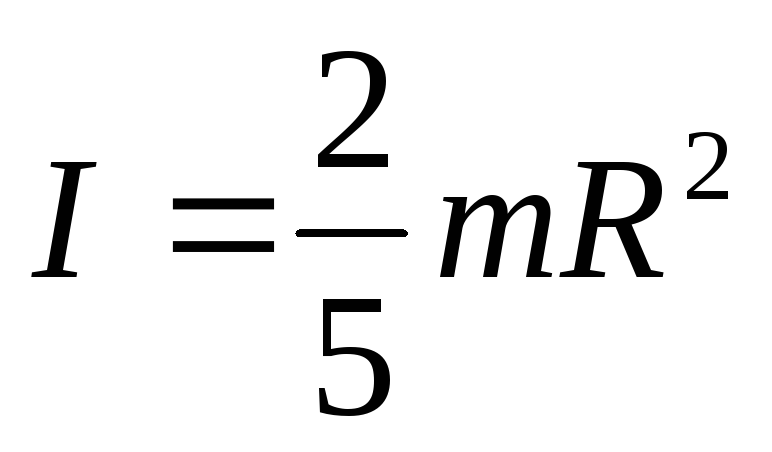
Моментом импульса материальной точки называется векторная величина равная произведению радиус вектора на импульс материальной точки .

Момент импульса вращающегося твердого тела можно вычислить как произведению момента инерции тела I на вектор угловой скорости угловую скорость его вращения .

Аналогия между поступательным и вращательным движениями приведена в таблице.

Поступательное движение		Вращательное движение вокруг неподвижной оси		Соотношение между соответствующими величинами
путь	S	Угол поворота
скорость		Угловая скорость
ускорение		Угловое ускорение		(тангенциальное ускорение)
сила		Момент силы
масса	m	Момент инерции	I
импульс		Момент импульса
Второй закон Ньютона		Основной закон динамики вращательного движения		_________
Кинетическая энергия		Кинетическая энергия		___________

3