ГОС / 45

45. Колебания кристаллической решетки.

3.1. Колебания одномерной цепочки упруго-связанных атомов. Закон дисперсии. Фазовая скорость упругих волн.

Рассмотрим цепочку из одинаковых атомов с массами , между которыми действуют упругие силы (рис.6).

Б удем учитывать только взаимодействие соседних атомов. Крестиками на рисунке обозначены равновесные (идеальные) расположения атомов: , , - отклонения соответствующих атомов от равновесных положений.

Силы упругости между атомами возникают при изменении расстояний между ними, поэтому сила, действующая на n атом со стороны n+1, может быть записана (закон Гука)

=-(-)

и аналогично для силы, действующей на n атом со стороны n-1 имеем

=-(-),

где -коэффициент упругости, то есть силы пропорциональны изменению расстояний между атомами. Рассматривая задачу классически, запишем второй закон Ньютона для атома n узла

или

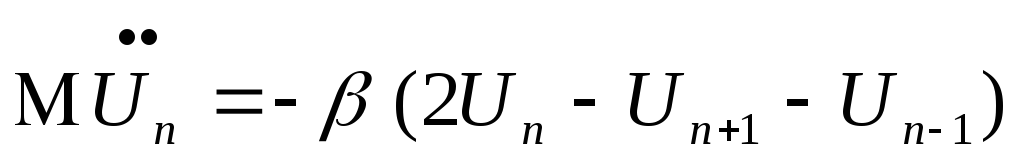(3.1)

Решение (3.1) можно искать в виде бегущей по цепочке монохроматической волны

= (3.2)

Подставляя (3.2) в (3.1), получим

-=-()

или

=()

По формуле Эйлера

следовательно, (3.3)

Выражение (3.2) является решением (3.1), если удовлетворяется условие (3.3), то есть

(3.4)

Проанализируем смысл решения (3.2) и соотношения (3.4). Величина na дает координату равновесного расположения n атома. Если вместо na писать x, то выражение

(3.5)

о писывает плоскую монохроматическую волну, бегущую в направлении оси x, где Α-амплитуда волны, q-волновое число , - частота волны. Фазовая скорость волны определяется выражением v_ф, групповая скорость v_гр. В отличие от (3.5), описывающего волну в непрерывной среде (координата x имеет любое значение), выражение (3.2) описывает волну в дискретной среде. Однако и в данном случае можно ввести понятие волнового числа, частоты, фазовой и групповой скоростей. Соотношение (3.4) устанавливает связь между частотой и волновым числом (длиной волны) упругой волны в цепочке атомов и оно носит название закона дисперсии. Задавая волновое число с помощью закона дисперсии (3.4) можно определить частоту волны и восстановить решение (3.2). Поскольку волны в кристалле с волновыми числами, отличающимися на тождественны (это непосредственно видно из (3.2) и (3.4)), то как и для электронов закон дисперсии можно рассматривать только в пределах первой зоны Бриллюэна, то есть от до (рис. )

=-предельная частота упругих волн цепочки атомов. При малых значениях q (длинные волны), когда , и частота пропорциональна волновому числу =

При этом фазовая скорость равна групповой v_ф = v_гр = (3.6)

Скорость продольных упругих волн, следовательно, пропорциональна корню квадратному из отношения модуля упругости к массе атома в цепочке.