§ 3. Дифференцирование суммы, произведения, частного

Теорема1 (дифференцирование суммы). Пусть, причем

Доказательство. Пусть.

Тогда, если , то, откуда

.

Так как по условию ,, то из теоремы о пределе суммы и последнего равенства получим утверждение теоремы 4.

Теорема2 (дифференцирование произведения). Пусть, причем.

Доказательство. Как и в предыдущем доказательстве, если, получим, откуда

. (1)

Поскольку из условий теоремы имеем ,,, то утверждение теоремы следует из равенства (1).

Вставка 1.

Теорема3 (производная частного). Пустьи. Тогда, причем.

Доказательство. Так как функциянепрерывна в точкеи, то по лемме о сохранении знака функции, имеющей предел, получим, что> 0:, если. Тогда в этом случае, если, получим

,

откуда

.

Отсюда, как и при доказательстве предыдущей теоремы, заключаем о справедливости теоремы 3.

Вставка 2.

Заметим, что из теорем 1 – 3 в предположении дифференцируемости функций в точке получим равенства для дифференциалов:

,,

. (2)

Вопросы и упражнения

1.Привести пример, показывающий, что утверждение, обратное теореме 1, может оказаться неверным.

2. То же для теорем 2 и 3.

3.Показать, что если функциядифференцируема в точкеи- константа, то имеет место равенство

4.Найти.

5.Обосновать соотношения (2).

§ 4. Дифференцирование обратной и сложной функций

Теорема1 (дифференцирование обратной функции). Пусть функцияопределена, непрерывна и строго монотонна в, причем. Тогда обратная функцияимеет производную в точке, причем.

Доказательство. По теореме 5 (гл.IY§ 2) обратная функция определена и непрерывна в некоторой окрестности точки- образапри отображениии, значит, еслигде,, то условияиравносильны.

Далее, . При() из условия теоремы существует предел правой части, а значит, по теореме о пределе частного существует предел левой части, причем

.

Но Поэтому.

Замечания.1) Эта теорема допускает наглядную геометрическую интерпретацию. Как известно,, где- угол, образованный касательной графика функцииfв точке (x₀,y₀) с осьюОХ, а, где- угол, образованный той же касательной с осьюOY.Очевидно,, поэтому.

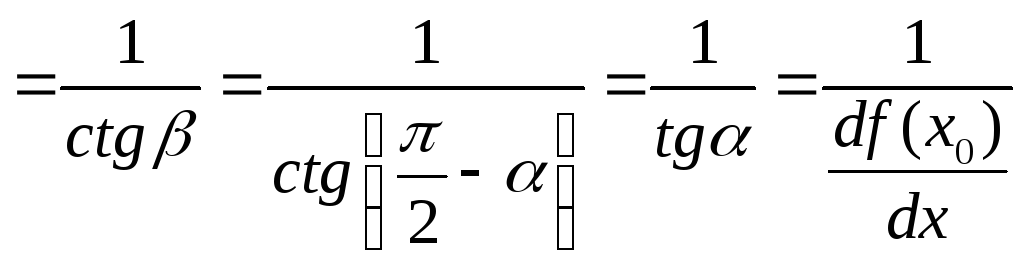x₀

X





2) Аналогично можно показать, что если функция fнепрерывна и строго монотонна в некоторой окрестности точк х₀и если в этой точке существует производная, то обратная функцияимеет в точкебесконечную производную.

3) Те же утверждения имеют место и для односторонних производных.

Вставка 1.

.

Теорема2 (дифференцирование сложной функции). Пусть функцияимеет производную в точке, а функцияимеет производную в точке. Тогда сложная функцияимеет производную в точке, причем

Замечание.Опуская значения аргументов, эту формулу можно переписать в виде

Доказательство. Так как функцииинепрерывны соответственно в точкахи( теорема 2,§1), то сложная функция, определенная в некоторой окрестности точки, непрерывна в этой точке ( теорема 4, гл.IY, § 1). Из дифференцируемости функций будем иметь

, где

, где

Поэтому

Когда , то, а в силу непрерывности функциив точкеимееми, следовательно,при. Тогда из последнего соотношения и соответствующих теорем о пределах функций получим

что и требовалось доказать.

Замечания.1)Теорема по индукции распространяется на суперпозицию любого конечного числа функций. Так, например, если, то(, в предположении, что все производные существуют в соответствующих точках.

2. Теорема остается верной и для односторонних производных.

3. В условиях теоремы 2 . А так каки, то. Таким образом.

=,

т.е. форма записи (первого) дифференциала не зависит от переменных. Это свойство называется инвариантностью формы первого дифференциала относительно выбора переменных.

Вставка 2.

В заключение этого пункта приведем таблицу производных основных элементарных функций:

1. ; 2.;

3. ,

4. ,

5. ,6.,

7. 8.

9. для значений, для которых обе части равенства имеют смысл;

10. ,

11. ,

Заметим, что из приведенной таблицы производных и правил дифференцирования вытекает, что производная любой элементарной функции есть функция элементарная, т.е. операция дифференцирования не выводит из класса элементарных функций.

Вопросы и упражнения

1.Вывести формулы для производных из приведенной выше таблицы, не рассмотренные в примерах.

2. Написать таблицу дифференциалов для основных элементарных функций.

3. Обосновать замечания 1 и 2 после теоремы 2.

4. Найти, если функцияопределяется уравнением.

5. Найти, если- показательно-степенная функция.