
дифференциальное исчисление
.pdf
|
|
|
|
|
|
|
|
|
41 |
P (x) c |
x x n c |
x x |
n 1 c |
x x |
n 2 ... c x x c , |
||||
n |
n |
0 |
n 1 |
0 |
n 2 |
0 |
1 |
0 |
0 |
|
|
|
|
|
cn 0 , |
|
|
|
(33.1) |
Найдем |
коэффициенты |
ck . |
Для |
этого продифференцируем |
обе |
части равенства |
|||
(33.1) раз.
|
|
n |
|
|
|
|
|
k 1 |
|
|
||||
Pn (x) k ck x x0 |
|
|
|
|||||||||||
|
|
|
|
|
||||||||||
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
k 2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Pn (x) k (k 1) ck x x0 |
|
(33.2) |
||||||||||||
|
|
k 2 |
|
|
|
|
|
|
|
|
|
|||
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(n) |
(x) |
n (n 1) (n 2)...2 1 cn |
|
|||||||||||
Pn |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставляя x x0 в (33.1) и (33.2), получаем |
|
|
||||||||||||
|
P (x ) c |
|
|
|
|
|
||||||||
|
n 0 |
|
|
0 |
|
|
|
|
|
|
||||
|
Pn (x0 ) c1 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Pn (x0 ) 2 c2 |
|
|
|
|
|
||||||||
|
... |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
P |
(n) (x ) n! c |
n |
|
|
|||||||||
|
|
n |
0 |
|
|
|
|
|
||||||
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
1 |
P(k ) |
|
|
|
|
|
|
||||||
(x ) , k 0, n . |
|
(33.3) |
||||||||||||
|
|
|||||||||||||
|
k |
k! |
|
n |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Подставляя (33.3) в (33.1), получаем |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
n |
(k ) |
(x0 ) |
|
|
|
|
|
|
|||
Pn (x) |
P n |
|
(x x0 )k . |
(33.4) |
||||||||||
|
|
|
||||||||||||
|
|
k 0 |
|
k! |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
Формула (33.4) называется формулой Тейлора для многочленов. |
||||||||||||||
Пример. Разложить многочлен P (x) 3 x2 5x 8 |
по степеням (x 1) . |
|||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
P2 (1) 0, P2 (x) 6 x 5, |
|
P2 (1) 11, |
P2 (x) 6, |
P2 (1) 6. |
||||||||||
f(x) 0 11(x 1) 62 (x 1)2 11(x 1) 3(x 1)2 .
33.2.Формула Тейлора для функции одного переменного
Пусть |
дана функция |
|
|
|
, |
|
которая |
|
раз дифференцируема в интервале |
|||||||
, |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Составим многочлен n -ой степени |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
n |
|
(k ) |
(x0 ) |
|
|
|
|
|
|||
|
|
Qn (x) |
|
f |
|
(x x0 )k . |
(33.5) |
|||||||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
k 0 |
|
k! |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
По формуле (33.3) c |
f (k ) (x ) |
|
1 |
|
|
Q(k ) (x ) , т.е. |
|
|||||||||
|
0 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||
|
k |
k! |
|
|
|
k! |
|
n |
0 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||||||
|
|
Q(k ) |
(x ) f |
(k ) (x ) k 0, n . |
(33.6) |
|||||||||||
|
|
n |
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
Таким образом, в точке |
многочлен Qn (x) |
и функция f (x) |
имеют одинаковые |
|||||||||||||
значения, производные k -го порядка многочлена и функции в точке |
также совпадают. |
|||||||||||||||
В точках, отличных от , такое равенство может не выполняться. Обозначим
Rn 1 (x) f (x) Qn (x) .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
42 |
Отсюда и из (33.5) получаем формулу |
|
|
|
|
|
|||||||||
|
|
|
n |
(k ) |
(x0 ) |
|
|
|
|
|||||
f (x) |
f |
|
|
(x x0 )k Rn 1 (x) . |
|
(33.7) |
||||||||
|
|
|
|
|
|
|||||||||
|
|
|
k 0 |
|
k! |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Формула (33.7) называется формулой Тейлора. Функция Rn 1 (x) называется остат- |
||||||||||||||
ком (остаточным членом). |
Про функцию говорят, что она разложена по степеням |
|||||||||||||
(x x0 ) , или, что она разложена по формуле Тейлора в окрестности точки . |
|
|||||||||||||
При x0 0 из формулы Тейлора (33.7) получаем формулу |
|
|||||||||||||
|
|
|
|
|
n |
|
f |
(k ) |
(0) |
|
|
|
||
|
f (x) |
|
xk Rn 1 (x) , |
|
(33.8) |
|||||||||
|
|
|
|
|||||||||||
|
|
|
|
k 0 |
|
k! |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
которую называют формулой Маклорена. |
|
|
|
|
|
|||||||||
Теорема (формула Тейлора с остатком в форме Пеано). Если функция |
диффе- |
|||||||||||||
ренцируема n раз в точке x0 , то в некоторой окрестности этой точки верна формула |
||||||||||||||
n |
(k ) |
(x0 ) |
(x x0 )k o (x x0 )n , |
|
|
|||||||||
f (x) |
f |
|
x x0 . |
(33.9) |
||||||||||
|
|
|
||||||||||||
k 0 |
k! |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Формула (33.9) называется формулой Тейлора с остаточным членом в форме Пеано.
Доказательство. Пусть функция |
|
дифференцируема n раз в точке x0 . |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
(33.7) |
|
|
|
|
|
n |
(k ) |
(x0 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Rn 1 (x) |
f (x) |
f |
|
|
(x x0 )k f (x) Qn (x) , |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
k! |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
R(k ) (x) f (k ) (x) Q(k ) |
(x) . |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
Тогда с учетом (33.6) получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Rn 1 (x0 ) 0 , |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
R(k ) |
(x ) f (k ) (x ) Q(k ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
(x ) 0 |
k 1, n . |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
n 1 |
0 |
|
|
|
|
|
0 |
|
|
|
n |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Применяя правило Лопиталя, получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
lim |
R (x) |
|
0 |
|
|
|
|
|
R (x) |
|
|
0 |
|
lim |
|
|
|
|
R (x) |
|
0 |
|||||||||||||||
n 1 |
|
|
lim |
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
... |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x x0 |
(x x0 )n |
0 |
x x0 |
|
|
n (x x0 )n 1 |
|
|
0 |
|
x x0 |
|
n (n 1)(x x0 )n 2 |
0 |
||||||||||||||||||||||
|
|
|
|
lim |
|
|
|
|
Rn(n1) (x) |
|
|
|
|
|
|
|
Rn(n1) (x0 ) |
0 |
|
|
|
|||||||||||||||
|
|
|
|
n(n 1)(n 2)...2 1 |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
x x0 |
|
|
|
|
n! |
|
|
|
|||||||||||||||||||||||
Представление (33.9) единственно. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Теорема (формула Тейлора с остатком в форме Лагранжа). Если функция диф- |
||||||||||||||||||||||||||||||||||||
ференцируема n раз в точке x0 |
и имеет в некоторой окрестности этой точки производную |
|||||||||||||||||||||||||||||||||||
f (n 1) , то верна формула |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
n |
|
f |
(k ) |
(x0 ) |
|
|
|
|
|
|
|
|
|
|
|
f |
(n 1) |
( ) |
|
|
|
|
|
|
|
|||||
|
|
f (x) |
|
(x x0 )k |
|
|
|
|
(x x0 )n 1 , |
|
(33.10) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
k 0 |
|
|
|
k! |
|
|
|
|
|
|
|
|
|
|
|
|
|
(n 1)! |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где x0 |
(x x0 ), |
|
0 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Формула (33.10) называется формулой Тейлора с остаточным членом в форме Ла- |
||||||||||||||||||||||||||||||||||||
гранжа. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример. Разложить функцию f (x) e3x 1 |
по формуле Тейлора в окрестности точки |
|||||||||||||||||||||||||||||||||||
x 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
43 |
► x 1, |
f (1) e4 , |
f (x) 3e3 x 1, |
f (1) 3e4 , |
f (x) 9e3 x 1, |
f (1) 9e4 , …, |
|||
0 |
|
|
|
|
|
|
|
|
f (k ) (x) 3k e3 x 1, |
f (k ) (1) 3k e4 . Применяя формулу (33.7), получаем |
|
||||||
|
|
|
n |
k |
4 |
|
|
|
|
|
|
f (x) |
3 e |
|
(x 1)k Rn 1 (x) ◄ |
|
|
|
|
|
k! |
|
|
|||
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
33.3.Разложение по формуле Маклорена некоторых функций
|
n |
|
|
x |
k |
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
x |
3 |
|
|
|
|
|
|
x |
n |
|
|
|
|
|
|
|
|
|
|
||||
1. |
ex |
|
|
Rn 1(x) 1 x |
|
|
|
... |
|
|
Rn 1(x) . |
|
|
|||||||||||||||||||||||||||||||
k! |
|
|
|
|
|
n! |
|
|
||||||||||||||||||||||||||||||||||||
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2! |
3! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
n |
|
|
( 1) |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2. |
sin x |
|
|
|
x2 k 1 R2 n 3 (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
k 0 |
(2 k 1)! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
x3 |
|
x5 |
|
|
x7 |
( 1)n |
x2 n 1 R |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
(x) . |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
3! |
|
|
5! |
|
|
|
7! |
|
|
(2 n 1)! |
|
|
|
|
|
|
|
|
|
|
2 n 3 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
n |
|
|
( 1) |
k |
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
x |
4 |
|
|
|
|
x |
6 |
|
|
|
( 1) |
n |
||||||||
3. |
cos x |
|
|
|
x2 k R2 n 2 |
(x) 1 |
|
|
|
|
|
|
... |
|
||||||||||||||||||||||||||||||
(2k)! |
|
|
|
|
|
|
|
|
|
|
(2n)! |
|||||||||||||||||||||||||||||||||
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
2! |
|
|
4! |
|
|
|
|
|
6! |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
n |
|
( 1) |
k 1 |
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
x |
3 |
|
|
|
|
( 1) |
n 1 |
|||||||||||
4. |
ln(1 x) |
|
|
|
xk Rn 1(x) x |
|
|
|
|
|
|
|
... |
|
|
|||||||||||||||||||||||||||||
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
n |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
n |
|
m(m 1)(m 2)...(m k 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
5. |
(1 x)m 1 |
xk |
Rn 1(x) |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
k! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x2 n R2 n 2 (x) .
xn Rn 1(x) .
|
|
1 |
m |
x |
m(m 1) |
x2 |
... |
m(m 1)(m 2)...(m n 1) |
|
xn R |
(x) . |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
1! |
|
2! |
|
|
|
|
|
|
|
|
|
|
|
|
|
n! |
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1 |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. |
( 1)k xk |
Rn 1(x) 1 x x2 x3 |
... ( 1)n xn Rn 1(x) . |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
1 x |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
k |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
n |
|
|
x |
2 k 1 |
|
|
|
|
|
|
|
x |
3 |
|
|
x |
5 |
|
|
|
|
|
|
x |
2 n 1 |
|
|
|
|
||||
7. |
arctg x ( 1)k |
|
|
|
|
R2 n 2 (x) x |
|
|
|
|
... ( 1)n |
|
|
|
R2 n 2 (x) . |
|
|
|||||||||||||||||||||
2 k 1 |
|
|
|
|
2 n 1 |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
k 0 |
|
|
|
|
3! |
5! |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
33.4. Приближенное вычисление функций с помощью формулы Тейлора |
|
|
||||||||||||||||||||||||||||||||||||
Рассмотрим на примере. Вычислим |
|
|
|
|
|
с точностью |
|
. |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
( 1) |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
sin 0,1 |
|
|
|
(0,1)2 k 1 R2 n 3 (0,1) . |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
(2 k |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
k 0 |
1)! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|||||||||||||||||||||||||||||
Найдем, сколько слагаемых достаточно взять, чтобы |
R2 n 3 (0,1) |
|
|
|||||||||||||||||||||||||||||||||||
Возьмем остаточный член в форме Лагранжа: |
|
|
|
|
|
|
, |
где |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
, |
|
|
|
. Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Поскольку производные |
функции |
|
|
|
|
|
|
равны либо |
|
, |
либо |
, |
то |
|||||||||||||||||||||||||
|
|
|
|
|
и, следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Найдем, при каких |
|
будет выполнено неравенство |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
или неравенство
(33.11)
|
|
|
|
|
44 |
При |
из (33.11) получаем: |
|
или |
. Неравенство выполнено. Тогда |
|
|
|||||
|
|
. Таким образом, |
с точностью 0,001◄ |
||
|
|
||||
34.Исследование функций и построение графиков
34.1.Монотонность функций
Теорема (об условиях монотонности). Пусть |
|
, |
непрерывна на отрезке |
|||||
и дифференцируема в интервале |
|
. Тогда |
|
|
|
|
||
1. |
|
|
|
на |
. |
|
|
|
2. |
|
|
возрастает на |
. |
|
|
||
3. |
|
|
убывает на |
|
. |
|
|
|
4. |
|
|
не убывает на |
. |
|
|
||
5. |
|
|
не возрастает на |
. |
|
|
||
Доказательство |
|
|
|
|
|
|
|
|
1. Необход имость . Пусть |
|
|
|
. |
Возьмем |
произвольную |
точку |
|
|
и рассмотрим |
. По теореме Лагранжа (п. 31) |
|
|
||||
|
. Следовательно, |
|
|
|
. |
|
|
|
Достаточность . Пусть |
|
|
на |
. Тогда |
. |
|
||
2. Пусть |
|
. Рассмотрим произвольный отрезок |
. По |
|||||
теореме Лагранжа |
|
|
|
|
|
. Поскольку |
, |
|
то |
. Следовательно, |
возрастает. |
|
|
||||
3.Доказывается аналогично 2.
4.Необход имость . Доказывается аналогично 2.
Достаточность . Пусть |
не убывает на |
. Тогда |
|
: |
|
|
будет выполнено |
. |
Следовательно, |
f (x ) lim |
f (x2 ) f (x1 ) |
0 . |
|
|
||||||
|
|
|
1 |
x2 x1 |
x2 x1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
Так как - произвольное число из |
, то |
|
. |
|
|
|
5.Доказывается аналогично 4
34.2. Необходимое и достаточные условия существования экстремума |
|
||||
Теорема 1 (необходимое условие). Если |
- точка локального экстремума |
||||
функции |
, то либо |
, либо производная функции в точке |
не суще- |
||
ствует. |
|
|
|
|
|
Доказательство. Если |
дифференцируема в |
, то по лемме Ферма |
|
||
|
|
|
|
|
|
Например, функция |
не имеет производную в точке |
, но |
- точка |
||
локального минимума функции. |
|
|
|
|
|
Определение. Точки, в которых производная функции обращается в нуль, называются стационарными. Стационарные точки и точки, в которых производная функции не существует, называются критическими (или подозрительными на экстремум).
Теорема 2 (достаточное условие 1). Пусть |
- дифференцируема в |
, |
|
за исключением может быть точки |
. Пусть |
- точка, подозрительная на экс- |
|
тремум. Тогда |
|
|
|

|
|
|
|
|
|
|
45 |
|
1. |
Если |
меняет знак при переходе через точку |
|
с «-» на «+», то |
- точка |
|
|
|
локального максимума. |
|
|
|
||
|
2. |
Если |
меняет знак при переходе через точку |
|
с «+» на «-», то |
- точка |
|
|
|
локального минимума. |
|
|
|
||
|
3. |
Если |
не меняет знак при переходе через точку |
, то в этой точке экстре- |
|||
|
|
мума не существует. |
|
|
|
|
|
|
Теорема 3 (достаточное условие 2). Пусть |
- дважды дифференцируема |
|||||
в |
, |
|
- точка, подозрительная на экстремум, и |
|
. Тогда |
|
|
|
1. |
Если |
, то |
- точка локального минимума. |
|
|
|
|
2. |
Если |
, то |
- точка локального максимума. |
|
|
|
Доказательство. Докажем утверждение 1. Пусть |
- точка, подозрительная на экс- |
||||||||||||||||||
тремум. Так как функция дифференцируема в |
, то по лемме Ферма |
|
. По |
||||||||||||||||
формуле Тейлора (33.10) с остаточным членом в форме Лагранжа получаем |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) f (x ) f (x |
|
)(x x |
|
) |
f ( ) |
(x x )2 |
|
f (x |
|
) |
f ( ) |
(x x |
|
)2 |
, |
|||
|
0 |
0 |
|
0 |
|
0 |
|||||||||||||
|
0 |
|
|
|
2! |
|
0 |
|
|
|
2! |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
где x |
(x x ), |
0 1. Тогда |
f (x) f (x ) |
|
( ) |
(x x )2 |
. Таким образом раз- |
||||||||||||
|
|
|
|||||||||||||||||
0 |
0 |
|
|
|
|
|
|
|
0 |
|
|
2! |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ность, f (x) f (x0 ) имеет тот же знак, |
что и вторая производная f ( ) . При значениях , |
||||||||||||||||||
достаточно близких к |
, разность |
|
|
, |
имеет тот же знак, что и |
. Пусть |
|||||||||||||
|
. Тогда |
|
|
. При |
|
функция убывает. При |
|
|
|
функция воз- |
|||||||||
растает |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
34.3.Выпуклость и вогнутость функции. Точки перегиба
Определение. Функция |
называется выпуклой вверх (вниз) |
|
на интервале |
, если каждая дуга графика этой функции лежит |
|
выше (ниже) стягивающей ее хорды. |
||
На рис. 34.1 изображена выпуклая вверх функция. |
||
Точка |
называется точкой перегиба кривой |
|
, если при переходе через эту точку кривая меняет направление выпуклости.
y |
x |
O |
Рис. 34.1 |
Теорема (необходимое и достаточное условие выпуклости). Пусть |
, |
|||||||
|
и |
дважды дифференцируема в |
. Для того чтобы функция |
была |
||||
выпукла вверх (вниз) на |
, необходимо и достаточно, чтобы |
|
|
|
||||
|
. |
|
|
|
|
|
|
|
Теорема (о точке перегиба). Пусть |
, |
и |
дважды диффе- |
|||||
ренцируема в |
. |
|
|
|
|
|
|
|
1) |
Если |
- точка перегиба кривой |
, то |
. |
|
|
||
2) |
Если |
|
и |
меняет знак при переходе через точку |
, то - |
|||
|
точка перегиба кривой |
. |
|
|
|
|
||
Замечание. Вторая производная может в точке перегиба не существовать, но функция в точке перегиба должна быть определена.

46
34.4.Асимптоты
Определение. Прямая |
называется асимпто- |
|
M |
|||
|
|
|
|
|
y |
|
той кривой |
, если расстояние от точки , при- |
f (x) |
||||
надлежащей этой кривой, до прямой |
стремится к ну- |
|
|
|||
лю при стремлении точки в бесконечность (рис. 34.2). |
|
|
||||
Различают вертикальные, горизонтальные и на- |
(l) |
|||||
|
|
|||||
клонные асимптоты. |
|
|
|
Рис. 34.2 |
||
Уравнение наклонной асимптоты: |
|
|
||||
|
|
|
|
, |
|
(34.1) |
где k lim |
f (x) |
, b lim f (x) k x . |
|
|
|
|
x |
|
|
|
|||
x |
x |
|
|
|
|
|
Горизонтальная асимптота является частным случаем наклонной. Ее уравнение по- |
||||||
лучаем по формуле (34.1) при |
. |
|
|
|
||
Если |
lim |
f (x) или |
lim |
f (x) , то кривая |
|
имеет вертикальную |
|
x x0 0 |
|
x x0 0 |
|
|
|
асимптоту . Кривая имеет вертикальные асимптоты, например, в точках бесконечного разрыва функции.
Пример. Найти асимптоты кривой |
|
y |
x3 4 |
, если они есть. |
||||||||||||||||
|
x2 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) |
lim |
x3 4 |
. Следовательно, |
|
x 0 - вертикальная асимптота. |
|||||||||||||||
x2 |
|
|
||||||||||||||||||
|
x 0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(34.1) |
x |
3 |
4 |
|
(34.1) |
x |
3 |
4 |
|
|
|
4 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2) |
k |
lim |
|
|
|
|
|
1, b |
|
lim |
|
|
|
|
x |
lim |
|
|
0 . |
|
|
|
x |
3 |
|
x |
2 |
|
2 |
||||||||||||
|
|
x |
|
|
|
|
|
x |
|
|
|
x x |
|
|
||||||
Таким образом, кривая имеет наклонную асимптоту: y x ◄
34.5.Наибольшее и наименьшее значения функции на отрезке
Пусть функция определена и непрерывна на отрезке . По теореме Вейерштрасса (п. 19) существуют наибольшее и наименьшее значения функции на этом отрезке. Функция может достигать наибольшего и наименьшего значений внутри отрезка или на
его концах. Если функция достигает наибольшего значения |
внутри отрезка |
, то - |
|||||
локальный максимум. Если функция достигает наименьшего значения |
внутри отрезка |
||||||
, то - локальный минимум. Поэтому для отыскания наибольшего и наименьшего |
|||||||
значения нужно |
|
|
|
|
|
|
|
1) |
найти точки , ,…, «подозрительные» на экстремум; |
|
|
||||
2) |
найти значения функции в этих точках: |
, |
,…; найти значения функции |
||||
|
на концах отрезка: |
, |
; |
|
|
|
|
3) |
сравнив полученные значения, найти наибольшее и наименьшее. |
|
|
||||
Пример. Найти наибольшее и наименьшее значения функции |
|
на |
|||||
. |
|
|
|
|
|
|
|
1) |
y 2 x , следовательно, |
x 0 - точка, «подозрительная» на экстремум, |
f (0) 4 . |
||||
47
2) f ( 1) 3, f (2) 0 .
3) |
, |
◄ |
34.6.Общая схема исследования функции и построения графиков
1. Область определения функции |
. |
2.Четность и периодичность.
3.Непрерывность. Вертикальные асимптоты.
4.Наклонные асимптоты.
5.Точки пересечения с осями координат.
6.Промежутки возрастания и убывания, экстремумы.
7.Направление выпуклости и точки перегиба.
8.Итоговая таблица.
|
f (x) |
x3 |
|
Пример. |
|
. |
|
(x 2)2 |
|||
1.Область определения функции: Df x R : x 2 .
2.Исследуем функцию на четность и периодичность.
|
f ( x) |
x3 |
|
||
Так как |
|
|
, |
то функция не является ни четной, ни нечетной. |
|
( x 2)2 |
|||||
|
(x T )3 |
T 0 . Следовательно, функция не является перио- |
|||
f (x T ) |
|
f (x) |
|||
(x T 2)2 |
|||||
дичной.
3.Исследуем функцию на непрерывность. Найдем вертикальные асимптоты, если они есть.
Функции f (x) x3 |
и |
f |
2 |
(x) (x 2)2 |
непрерывны при любом |
x . Так как |
1 |
|
|
|
|
|
|
f (2 0) , то в точке |
x 2 функция терпит бесконечный разрыв. Вертикальная |
|||||
асимптота: x 2 .
4.Найдем наклонные асимптоты.
k lim |
x2 |
|
1, |
b lim |
4 x2 |
4 |
4 |
. Следовательно, |
y x 4 - наклонная асим- |
|
|
|
|
||||||
x (x 2) |
2 |
|
x (x 2)2 |
|
|
|
|||
птота.
5.Точки пересечения функции с осями координат: (0, 0) .
6.Исследуем функцию на монотонность и найдем экстремумы функции, если они существуют.
x2 (x 6) |
|
|
|
|
x |
y (x 2)3 . |
|
0 2 |
6 |
|
|
|
|
|
|||
Критические точки: x 0, x 6, x 2 . |
|
|
|
|
|
Функция возрастает на интервалах ( , 2), |
(6, ) , |
убывает на интервале |
(2, 6) . |
||
Следовательно, x 6 - точка локального минимума. |
|
. |
|
|
|
6.Определим направление выпуклости графика и найдем точки перегиба, если они есть.
y |
24 x |
|
|
|
|
(x 2)4 . |
|
0 2 |
|
x |
|
На интервале ( , 0) функция выпукла вверх, на |
|
|
|
|
|
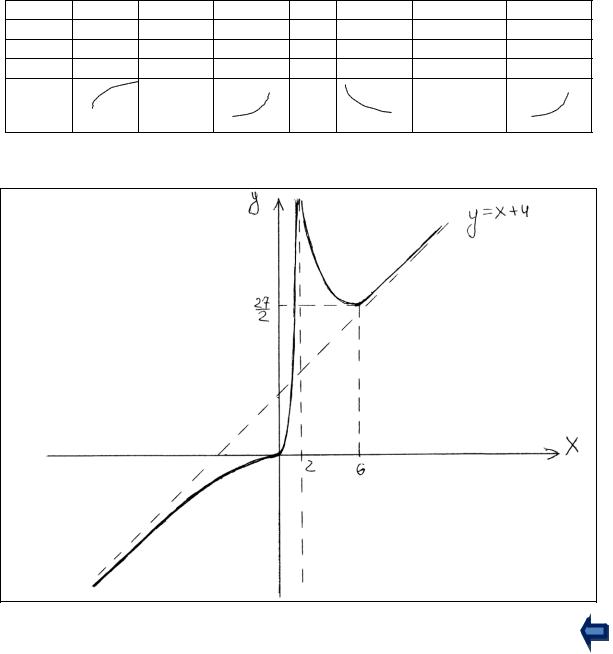
48
интервалах (0, 2), (2, ) выпукла вниз. Следовательно, точка x 0 является точкой перегиба функции.
7.Составим итоговую таблицу.
0 |
|
- |
|
+ |
+ |
|
+ |
|
+ |
+ |
+ |
точка |
|
|
точка |
перегиба |
|
|
|
8.Сделаем чертеж
