
дифференциальное исчисление
.pdf
31
20.Производная и дифференциал функции одного переменного
Определение. Пусть |
|
, |
|
|
|
, |
|
|
- предельная точка множества . |
|
|||||||||||||
Если существует конечный предел |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
lim |
f (x0 ) |
|
A , |
|
|
|
|
|
|
|
|
(20.1) |
||||
|
|
|
|
|
|
|
x 0 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||
то его называют производной функции |
в точке |
и обозначают |
, |
|
, |
. |
|||||||||||||||||
|
|||||||||||||||||||||||
Пример. Найти производную функции |
|
|
|
|
|
с помощью определения произ- |
|||||||||||||||||
водной. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x ) |
lim |
|
f (x x) f (x ) |
lim |
ex0 |
x ex0 |
|
|
|
|
|||||||||||
|
lim |
|
|
0 |
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|||||
|
|
|
x |
|
|
|
|
|
x |
|
|
|
|
|
x |
|
|
|
|||||
|
x 0 |
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|||
|
|
|
|
|
x |
|
|
e x |
1 |
|
x |
|
x |
x |
|
|
|
|
|
|
|||
|
|
|
|
|
e 0 lim |
|
|
|
e |
0 |
lim |
|
|
e 0 . |
|
|
|
|
|
||||
|
|
|
|
|
x |
|
x |
|
|
|
|
|
|||||||||||
|
x |
|
|
|
x 0 |
|
|
|
x 0 |
|
|
|
|
|
|
|
|||||||
Таким образом, e |
|
x |
► |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Определение. Если существует предел
lim f (x0 )
x 0 0 x
то |
его |
называют производной функции |
|
f (x ) |
f (x ) . |
||
|
0 |
|
0 |
|
lim |
f (x0 ) |
, |
(20.2) |
|
|
x |
|
|||
x 0 0 |
|
|
|
||
|
в точке |
|
|
слева (справа) и обозначают |
|
Лемма (об односторонних производных). Для того чтобы функция имела в точке производную необходимо и достаточно, чтобы f (x0 ) f (x0 ) . Причем
.
Пример. Найти производную функции f (x)
Решение. |
|
|
|
|
||
|
|
x, |
x 0, |
|
x |
0 |
|
x |
|
|
|||
|
|
x, |
x 0 |
|
|
|
Выясним, существует ли производная в точке |
||||||
но, в точке |
|
производная не существует► |
|
|||
x |
. |
|
|
|
|
|
x 0, |
|
|
1, |
|
f |
(x) |
x 0 |
|
|
|
1, |
|
|
|
|
|
0. |
f (0) 1, |
f (0) 1. Следователь- |
|
|
|
|
|
|
Определение. Функция |
называется дифференцируемой в точке |
, если ее при- |
||||
ращение в этой точке представимо в виде |
|
|
|
|
|||
|
|
|
|
, |
, |
|
(20.3) |
где |
, |
. |
|
|
|
|
|
|
Определение. Если функция дифференцируема в точке |
, то выражение |
|||||
называется дифференциалом функции |
в точке |
и обозначается |
: |
||||
|
|
|
|
. |
|
|
(20.4) |
|
Для независимой переменной положим по определению |
. Тогда (20.4) мож- |
|||||
но записать в виде |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
(20.5) |
|
Определение. Функция |
называется дифференцируемой на множестве , если |
|||||
она дифференцируема в каждой точке этого множества. |
|
|
|
||||

32
21.Связь между дифференцируемостью и существованием производной функции. Связь между дифференцируемостью и непрерывностью функции
Теорема 1 (о связи между дифференцируемостью и существованием производ-
ной). Для того чтобы функция |
была дифференцируема в точке |
, необходимо и доста- |
||||||||||||
точно, чтобы она имела конечную производную в точке |
. При этом |
|
||||||||||||
|
|
|
|
|
|
|
|
. |
|
|
|
|
(21.1) |
|
Доказательство. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Необходимость . Пусть |
дифференцируема в точке : |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
, |
|
. |
|
|
|
|
lim |
f (x0 ) lim |
|
A x o( x) |
A lim |
o( x) |
A. |
|
|||||||
|
|
x |
|
|||||||||||
x 0 |
x |
x 0 |
|
|
x |
|
|
x 0 |
|
|
||||
|
|
|
|
(20.5) |
|
|
|
|
|
|
|
|
||
Следовательно, f (x0 ) A, |
|
df (x0 ) |
|
f (x0 ) dx . |
|
|
|
|
|
|
|
|||
Достаточность . |
Пусть |
имеет производную в точке |
|
: |
|
|
||||||||
|
|
|
|
f (x ) lim f (x0 ) |
A . |
|
|
|
|
|
||||
|
|
|
|
0 |
|
x 0 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Обозначим f (x0 ) A . Выразим приращение функции: |
|
|
|
|
||||||||||
x |
|
f (x0 ) A x A x x . |
|
|
|
|
||||||||
|
|
|
|
|
(21.2) |
|||||||||
x o( x) при x 0 , так как |
|
|
|
|
|
|
|
|
|
|
||||
lim |
x |
|
|
|
f (x0 ) |
|
|
lim |
f (x0 ) |
A 0 . |
|
|||
x |
lim lim |
x |
A |
|
x |
|
||||||||
x 0 |
|
x 0 |
x 0 |
|
|
x 0 |
|
|
|
|||||
Следовательно, из (21.2) получаем |
|
|
|
|
|
|
|
|
|
|
||||
|
f (x0 ) A x o( x), |
x 0 |
|
|
|
|||||||||
Теорема 2 (о связи между дифференцируемостью и непрерывностью). Если |
||||||||||||||
функция дифференцируема в точке |
|
, то она непрерывна в этой точке. |
|
|||||||||||
Доказательство. По условию теоремы |
|
|
|
|
|
, |
. Отсюда |
|||||||
получаем: |
lim f (x0 ) lim A x o( x) 0 |
|
|
|
||||||||||
|
|
|
|
|||||||||||
|
x 0 |
|
x 0 |
|
|
|
|
|
|
|
|
|||
Замечание. В обратную сторону утверждение, вообще говоря, неверно. Непрерывная в точке функция может не иметь производную в этой точке. Например, функция непрерывна в точке , но производная функции в этой точке не сущест-
вует.
22.Свойства производной и дифференциала
Теорема 1. |
Если функции |
, |
дифференцируемы на множестве , |
||||
то |
|
|
|
|
|
||
1. |
|
|
; |
|
|
||
2. |
|
|
; |
|
|
||
3. |
|
|
|
|
, |
. |
|
|
|
|
|
||||
Доказательство. Докажем первое утверждение, например, для суммы. |
|||||
|
lim |
u v |
lim |
u(x x) v(x x) u(x) v(x) |
|
u v |
x |
x |
|||
|
x 0 |
x 0 |
|
||

|
|
|
|
|
|
|
|
|
33 |
lim |
u(x x) u(x) v(x x) v(x) lim |
u(x) lim |
v(x) u (x) v (x) |
||||||
x 0 |
|
|
|
x |
x 0 |
x |
x 0 |
x |
|
|
Следствие. |
|
|
, где |
, - константы. |
||||
Теорема 2. Если функции |
, |
|
дифференцируемы на множестве , |
||||||
то |
|
|
|
|
|
|
|
|
|
|
1. |
|
|
|
|
. |
|
|
|
|
2. |
|
|
|
|
. |
|
|
|
|
3. |
|
|
|
, |
. |
|
|
|
|
|
|
|
|
|
|
|||
Доказательство следует из формулы (21.1) и теоремы 1.
23.Производные основных функций
Пусть .
0
Примечание. , , , – гиперболиче-
ские косинус, синус, тангенс и котангенс. Для гиперболических синуса и косинуса верно тождество: . 
24.Дифференцирование сложной и обратной функции
Теорема 1 (о производной сложной функции). Пусть функция |
дифференци- |
||||
руема в точке , а функция |
дифференцируема в точке |
, причем |
. Тогда |
||
сложная функция |
|
дифференцируема в точке |
и |
|
|
|
|
|
|
. |
(24.1) |
Доказательство. |
Придадим точке |
приращение |
. Функция |
получит |
|
приращение |
, а функция |
получит приращение |
. Так как |
||
34
дифференцируема в точке , то она непрерывна в этой точке (п. 21). Следовательно,
lim u lim (x0 ) 0 (п. 16). Тогда |
|
|
|
|
|
|
|
|
||||||||
x 0 |
|
x 0 |
|
|
|
|
lim f (x0 ) lim f (u0 ) |
|
|
|||||||
|
|
|
|
z (x ) lim z(x0 ) |
|
|
||||||||||
|
|
|
|
|
0 |
x 0 |
x |
|
x 0 |
x |
|
x 0 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
lim |
f (u0 ) |
u |
lim |
f (u0 ) (x0 ) |
lim |
f (u0 ) |
lim |
(x0 ) |
f (u |
) (x ) |
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
u |
|
|
x |
u 0 |
u |
|
x 0 |
x |
0 |
0 |
||||
|
x 0 |
x |
x 0 u |
|
|
|
|
|||||||||
|
Инвариантность формы дифференциала |
|
|
|
|
|
|
|||||||||
|
Пусть выполнены условия теоремы 1. Тогда функция |
|
|
дифференци- |
||||||||||||
руема в точке |
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
(24.1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
dz(x0 ) z (x0 ) dx |
f (u0 ) (x0 ) dx f (u0 ) d (x0 ) f (u0 ) du . |
(24.2) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
d ( x0 ) |
|
|
du |
|
|
|
|
Таким образом, дифференциал функции имеет одинаковый вид независимо от того, является переменная независимой или нет. Это свойство дифференциала называется ин-
вариантностью формы дифференциала.
Теорема 2 (о производной обратной функции). Пусть функция непрерывна,
строго монотонна в некоторой окрестности точки и имеет отличную от нуля производ-
ную в точке . Тогда обратная функция |
|
имеет производную в точке |
, |
||
причем |
|
|
|
|
|
|
|
1 |
|
|
|
|
f 1 ( y0 ) |
|
|
. |
(24.3) |
|
|
|
|||
|
|
f (x0 ) |
|
||
Доказательство. По теореме об обратной функции из п. 19 функция |
имеет об- |
||||
ратную функцию |
, также непрерывную и строго монотонную в некоторой ок- |
||||
рестности точки |
. По условиям теоремы |
f (x0 ) lim |
f (x0 |
||
x |
|||||
|
|
|
x 0 |
||
функции |
в |
точке |
, |
||
) 0 . В силу непрерывности
lim x 0 . |
Тогда |
y 0 |
|
|
|
|
|
x |
|
1 |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f 1 |
( y0 ) lim |
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
y |
y |
|
|
|
|
y |
f |
(x ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
y 0 |
x 0 |
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
x |
|
|
x 0 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Примеры |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1. |
Найти производную |
|
|
|
|
|
|
|
|
. По теореме 2 получаем: y |
1 |
|
|
1 |
|
|
1 |
|
1 |
. |
||||||||||||||
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
e |
|
|
e |
|
|
x |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
ln x |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2. |
sin(3x |
2 |
|
|
|
|
|
|
|
2 |
2) по теореме 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
2) 6 x cos(3x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
3 |
|
|
log |
2 |
(7 x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
log34 (7 x) 3log42 (7 x) |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
◄ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
ln 4 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
7 x ln 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
25.Дифференцирование сложно-показательной функции
Пусть функции , - дифференцируемые функции. Функция называется сложно-показательной функцией. Найдем ее производную. Сна-
чала представим функцию в другом виде:
.

35
Тогда
.
Пример. Найти производную функции |
. |
►
◄
26.Дифференцирование неявной функции и функции, заданной параметрически
26.1.Дифференцирование неявной функции
|
Функция |
|
называется заданной неявно, если она задается уравнением: |
|
|||||
|
|
|
|
. |
|
(26.1) |
|||
|
Если из этого уравнения можно выразить через : |
, то говорят, что функ- |
|||||||
ция |
задана явно. |
|
|
|
|
|
|
||
|
Найдем производную |
|
|
. Продифференцируем обе части равенства (26.1) по , |
|||||
|
|
|
|||||||
учитывая, что |
зависит от |
. Затем из полученного равенства выразим . |
|
||||||
|
Пример. |
|
|
|
. Найти . |
|
|
||
|
►Продифференцируем обе части равенства по , учитывая, что зависит от |
: |
|||||||
и выразим : |
|
|
|
|
|
◄ |
|
|
|
|
|
|
|
|
|
|
|||
26.2.Дифференцирование параметрически заданной функции
x (t),
Пусть функция задана параметрически:
y (t).
Пусть (t) и (t) |
- дифференцируемые функции. Предположим, что функция (t) |
||||
имеет обратную функцию t 1 (x) . Тогда можно записать: y (t) 1 (x) . Найдем |
|||||
производную функции y по переменной x . |
1 |
(t) . |
|||
|
dy |
(t) 1 (x) |
(t) |
||
|
|
(24.1) |
(24.3) |
|
|
|
dx |
x |
|
(t) |
(t) |
|
|
|
|||
Или эту формулу можно записать так:
dy |
|
yt |
. |
(26.2) |
|
|
|||
dx |
|
x |
|
|
|
|
t |
|
|
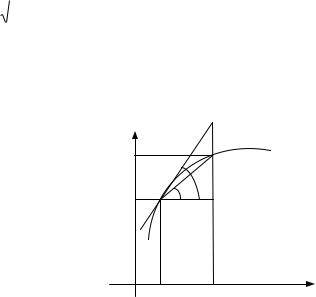
Пример. Найти , если функция задана параметрически:
► |
|
|
|
◄ |
|
|
|
||
|
|
|
|
|
36
27.Геометрический и физический смысл производной и дифференциала. Касательная и нормаль
27.1.Геометрический смысл
Пусть функция |
дифференцируема в точке |
. Обозначим: |
, |
||||||||
(рис. 27.1). Придадим точке x0 приращение x . Функция f (x) |
при этом получит при- |
||||||||||
ращение y . |
Пусть M x0 x, y0 y . |
Проведем |
|
секущую M 0 M кривой y f (x) . |
|||||||
Обозначим угол между секущей M 0 M и осью Ox через . Тогда |
|
|
. |
||||||||
|
|||||||||||
Определение. Касательной к кривой |
|
|
в точке |
называется предельное |
|||||||
положение секущей M 0 M при M M0 , если оно существует. |
|
|
|
||||||||
Так как |
дифференцируема в точке x0 , то она непрерывна в этой точке и по опреде- |
||||||||||
|
|
|
|
|
|
|
|||||
лению |
lim y 0 . Следовательно, M0 M |
|
x2 |
y2 |
|
0 при x 0 , то есть M M0 . |
|||||
|
x 0 |
|
|
|
|
|
|
|
|
|
|
Тогда |
f (x ) lim y |
lim tg tg , |
где |
- |
угол между |
касательной к кривой |
|||||
|
0 |
x 0 x |
M M0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y f (x) в точке x0 и осью Ox .
Таким образом, геометрический смысл производной заключается в том, что f (x0 ) tg .
Найдем геометрический смысл дифференциала. df (x0 ) f (x0 ) dx f (x0 ) x tg x AB . Таким об-
разом, дифференциал численно равен приращению ординаты касательной к кривой y f (x) в точке x0 .
|
Найдем уравнение касательной. Уравнение секу- |
||||||||
щей M 0 M запишем как уравнение прямой, проходящей |
|||||||||
через |
две точки M0 x0 , y0 |
|
и |
M x0 x, y0 y : |
|||||
|
x x0 |
|
y y0 |
. Отсюда: |
y y |
|
|
y (x x ) . Переходя |
|
|
|
|
0 |
||||||
|
x |
|
y |
|
|
x |
0 |
||
|
|
|
|
|
|
||||
|
B |
y |
y f (x) |
|
|
y0 y |
M |
M 0 |
|
|
|
y0 |
A |
x
x0 |
x0 x |
Рис. 27.1
к пределу при x 0 , получим уравнение касательной: y y0 f (x0 ) (x x0 ) .
Определение. Нормалью к кривой y f (x) в точке x0
дящая перпендикулярно касательной через точку касания.
Из уравнения (27.1) найдем координаты вектора
|
f (x0 ), 1 . Следовательно, уравнение нормали имеет вид: |
||
n |
|||
|
y y0 |
1 |
(x x0 ) . |
|
|
||
|
f (x0 ) |
||
|
|
|
|
(27.1)
называется прямая, прохо-
нормали к |
касательной: |
|||
x x0 |
|
y y0 |
или |
|
f (x ) |
1 |
|||
|
|
|||
0 |
|
|
|
|
|
|
|
(27.2) |
|
27.2.Физический смысл
Пусть |
- закон движения материальной точки. Тогда величина мгновенной |
||
скорости в момент времени равна |
. |
|
|
Расстояние, |
которое прошла бы |
материальная точка за время |
со скоростью |
, равно |
. |
|
|

37
28.Производные и дифференциалы высших порядков
Пусть функция |
дифференцируема на множестве |
. Тогда на множестве возника- |
|||||||
ет новая функция , которая сама может иметь производную |
. Если такая произ- |
||||||||
водная существует, то ее называют производной второго порядка функции |
и обозначают |
||||||||
. |
|
|
|
|
|
|
|
|
|
Определение. Производной |
-го порядка функции называется производная про- |
||||||||
изводной |
-го порядка: |
|
|
(если она существует). |
|
||||
Производные |
-го порядка обозначают еще |
|
. |
|
называется дифферен- |
||||
|
|
||||||||
Определение. |
Дифференциалом |
-го порядка функции |
|||||||
циал дифференциала |
-го порядка: |
|
|
|
|
(если он существует). |
|||
Найдем второй дифференциал функции . |
|
|
|
|
|
||||
|
|
|
|
|
|
|
. |
|
(28.1) |
Если |
- независимая переменная, то |
|
|
|
|
и из (28.1) следует: |
|||
|
|
|
|
|
|
|
. |
|
|
Аналогичная формула верна для дифференциала |
-го порядка: |
|
|||||||
|
|
|
|
|
, |
|
|
|
(28.2) |
если - независимая переменная. |
|
|
|
|
|
|
|
||
Если |
не является независимой переменной, а является функцией, |
зависящей, на- |
|||||||
пример, от |
: |
, то |
и |
. В этом случае из (28.1) получаем: |
|||||
|
|
|
|
|
|
|
. |
|
(28.3) |
Следовательно, дифференциал второго порядка не обладает свойством инвариантно-
сти.
29.Вторая производная функции, заданной параметрически
Пусть функция y y(x) задана параметрически: x (t), |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y (t). |
|
|
|
Предположим, что (t) |
имеет обратную функцию t 1 (x) . |
Тогда по формуле |
|||||||||||||
(26.2) имеем: y |
(t) . Функция y |
также может иметь производную. Найдем ее. |
|||||||||||||
|
|
x |
(t) |
|
|
x |
|
|
|
|
|
|
|
||
|
|
y |
|
|
|
|
|
|
t |
|
(t) (t) (t) (t) |
|
|
|
|
|
d |
|
|
d |
(t) |
(24.1) |
(t) |
|
(24.3) |
|
1 |
|
|||
|
|
x |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
xt |
|
||||||
|
dx |
|
|
dx |
|
(t) |
|
(t) t |
|
|
(t) |
|
|
||
(t) (t) (t) (t)
(t) 3 .
Кратко эту формулу можно записать следующим образом:
y |
|
y x x y |
|
||
tt t |
tt t |
. |
(29.1) |
||
x 3 |
|
||||
xx |
|
|
|
|
|
|
|
t |
|
|
|
38
30.Приближенное вычисление с помощью дифференциалов
Если функция дифференцируема в точке |
x0 , то |
при |
||
. По определению дифференциала |
. По теореме 1 из п. 21 |
. |
||
Пусть |
. Тогда |
и |
|
|
.
f (x0 ) ~ df (x0 ) при формулу f (x0 ) df (x0 ).
Пример. Дана функция f (x) x3 e x
► f (x1 ) df (x1 ) f (x1 ) x 3 x2 ex
. В приближенных вычислениях применяют
, x1 0 , x2 0,01.
0,01 0 0,01◄
x 0
31.Экстремумы
|
Определение. Пусть |
|
|
|
|
. Точка |
|
|
называется точкой локального |
||||||||
минимума (максимума) функции |
|
, если |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
. |
|
|
|
(31.1) |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
Точки локального минимума ( |
|
|
) и локального |
|
|
|
|
|
||||||||
максимума ( |
) |
называются точками |
локального |
|
|
|
|
|
|||||||||
экстремума ( |
). |
Значение |
функции |
в точке ло- |
|
a |
|
x2 |
x |
||||||||
кального минимума (максимума) называется локальным ми- |
|
|
|||||||||||||||
|
|
|
|
|
|||||||||||||
нимумом (локальным максимумом) функции. |
|
|
|
|
|
x1 |
x3 |
b |
|||||||||
|
Если в (31.1) выполняются строгие неравенства, то x0 |
|
|
|
|
|
|||||||||||
называется точкой строгого локального минимума (макси- |
|
|
|
Рис. 31.1 |
|
||||||||||||
|
|
|
|
|
|||||||||||||
мума). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Замечание. Функция может иметь локальный экстремум только во внутренних точ- |
||||||||||||||||
ках отрезка [a,b] . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
На рис. 31.1 показана функция, которая имеет два локальных максимума в точках x1 |
||||||||||||||||
и x3 и один локальный минимум в точке x2 . |
|
|
|
|
|
|
|
|
|||||||||
|
Лемма Ферма. Пусть |
|
|
|
, |
|
|
. Пусть функция |
дифференцируема |
||||||||
в точке |
. Если - точка локального экстремума, то |
f (x0 ) 0 . |
|
|
|
|
|||||||||||
|
Доказательство. Пусть |
|
- точка локального максимума, т.е. |
U (x0 ) [a,b] : |
|||||||||||||
f (x) f (x0 ) |
x U (x0 ) . |
Следовательно, |
f (x0 ) f (x) f (x0 ) 0 |
x U (x0 ) . |
Если |
||||||||||||
x x , то x x x 0 |
и |
f (x |
) |
lim |
f (x0 ) 0 . |
Если x x , |
то |
x x x |
0 и |
||||||||
|
0 |
|
0 |
|
|
0 |
x 0 0 |
x |
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
f (x ) |
lim |
f (x0 ) 0 . По лемме об односторонних производных производная в точке |
|||||||||||||||
|
0 |
x 0 0 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Следовательно, f (x0 ) 0 |
|||||||
x0 |
существует тогда и только тогда, когда |
|
|
|
|||||||||||||
|
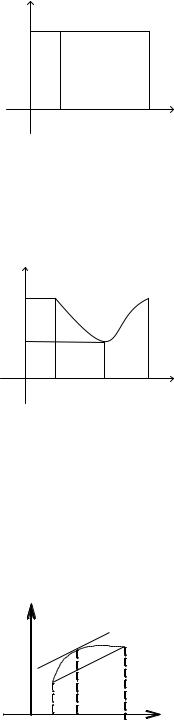
Геометрический смысл леммы Ферма. |
Если |
- точка локального экстремума и |
||||||||||||||
функция |
дифференцируема в точке |
, то касательная к графику функции в этой точке |
|||||||||||||||
параллельна оси Ox . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
39 |
Теорема Ролля. Пусть |
, |
- непрерывна на отрезке |
, дифферен- |
|
цируема в интервале |
и |
. Тогда |
. |
|
Доказательство. Пусть |
. Так как функ- |
ция непрерывна на отрезке |
, то по теореме Вейерштрасса |
(п. 19) она достигает на этом отрезке наибольшего и наименьшего значений. Обозначим , .
Рассмотрим возможные варианты поведения функции:
1) |
(рис. 31.2). |
В этом случае функция |
|
является постоянной и |
. |
y
m M A
A
x
O |
a |
b |
|
2) |
, |
(рис. 31.3). Здесь наименьшее значе- |
Рис. 31.2 |
|
ние функции достигается внутри отрезка |
. Это значит, что |
|
||
функция имеет локальный минимум в некоторой точке |
. По лемме Ферма в этой |
|||
точке производная равна нулю. |
|
|
||
3), . Этот случай аналогичен предыдущему. Функция имеет локаль-
ный максимум в интервале |
. |
4), . Функция имеет локальный максимум
и минимум в интервале |
. |
|
|
|
Геометрический смысл теоремы Ролля. Пусть функ- |
||
ция |
удовлетворяет на отрезке |
условиям теоремы |
|
Ролля. Тогда в интервале |
найдется хотя бы одна точка, |
||
вкоторой касательная к графику функции параллельна оси
.
y
A M m
A M
m
x
O |
a |
|
b |
|
Рис. 31.3
Теорема Лагранжа. |
Пусть |
, |
|
|
|
- непрерывна на отрезке |
и диф- |
|||||||||||
ференцируема в интервале |
. Тогда |
|
|
|
|
|
|
|
|
|
|
|
. |
|
||||
Доказательство. Обозначим |
|
|
|
|
и |
введем вспомогательную |
функцию |
|||||||||||
|
|
|
|
|||||||||||||||
|
|
|
|
. Функция |
непрерывна на отрезке |
|
|
, дифференци- |
||||||||||
руема в интервале |
и |
. |
По теореме Ролля |
|
|
|
. |
|||||||||||
Следовательно, |
, |
|
|
|
|
|
|
|
|
y |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
Геометрический смысл теоремы Лагранжа. Если |
|
|
|
|
||||||||||||||
|
|
|
|
|
||||||||||||||
функция |
удовлетворяет условиям теоремы, то в интер- |
|
|
|
|
B |
||||||||||||
вале |
|
существует хотя бы одна точка, в которой каса- |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|||||||||||||
тельная к графику функции в этой точке параллельна секу- |
|
|
|
|
|
|||||||||||||
щей |
(рис. 31.4). |
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
x |
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
b |
||
Теорема Коши. Пусть |
; |
, |
|
- не- |
|
|
||||||||||||
|
|
|
|
|
|
|||||||||||||
прерывны на отрезке |
и дифференцируемы в интервале |
|
|
|
Рис. 31.4 |
|
||||||||||||
, |
причем |
|
|
. Тогда |
|
|
|
|
|
|
|
|||||||
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство. Проводится с помощью вспомогательной функции |
|
|||||||||||||||||
|
|
|
, где |
|
|
, и теоремы Ролля |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
40
32.Раскрытие неопределенностей по правилу Лопиталя
Теорема. Пусть |
( |
). И пусть |
1) lim f (x) 0 , lim g(x) 0 ; |
|
|
x a |
x a |
|
2)функции f (x), g(x) дифференцируемы в интервале (a,b) ;
3)g (x) 0 x (a,b) ;
4) lim |
|
f (x) |
A , |
. |
|
|
||
|
|
|
|
|||||
x a |
|
g (x) |
|
|
|
|||
Тогда lim |
f (x) |
A . |
|
|
|
|||
|
|
|
|
|||||
|
x a |
g(x) |
|
|
|
|||
Доказательство. Доопределим функции |
и |
в точке a , положив f (a) g(a) 0 . |
||||||
Тогда по условию 1) теоремы функции f (x), |
g(x) |
будут непрерывны в точке a справа. |
||||||
Вследствие условия 2) f (x), |
g(x) непрерывны в интервале (a,b) . Следовательно, функ- |
|||||||
ции непрерывны на интервале [a, b) , т.е. непрерывны на отрезке [a, x] |
x [a,b) . По |
|||||||||||||||
теореме Коши (a, x) : |
f (x) f (a) |
|
|
f ( ) |
|
. Так как |
f (a) g(a) 0 , то |
|
f (x) |
|
f ( ) |
. |
||||
|
|
g(x) g(a) |
|
g ( ) |
|
|
|
g(x) |
|
g ( ) |
||||||
При x a a и lim |
f (x) |
lim |
f ( ) |
|
A |
|
|
|
|
|
|
|
||||
g(x) |
g ( ) |
|
|
|
|
|
|
|
||||||||
x a |
a |
|
|
|
|
|
|
|
|
|
|
|||||
Замечания
1) Теорему можно сформулировать для неопределенности . Вместо условия 1) будет
условие lim f (x) , lim g(x) . |
||
x a |
x a |
|
2) Если производные |
f (x), |
g (x) удовлетворяют условиям теоремы, то правило Лопи- |
таля можно применить еще раз и так далее.
3) С помощью правила Лопиталя можно раскрывать также неопределенности вида ( ), (0 ), 1 и другие. Для этого указанные неопределенности сводятся к не-
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
lim g(x) . То- |
|||
определенностям вида |
|
|
или |
|
. Например, пусть lim f (x) 0 , |
||||||||||||||||
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
x a |
x a |
|||
гда lim f (x) g(x) 0 lim |
|
f (x) |
|
|
0 |
|
|
||||||||||||||
|
|
|
|
|
|
|
. |
|
|||||||||||||
|
|
|
|
|
|
||||||||||||||||
x a |
|
|
|
|
|
|
|
|
x a 1/ g(x) |
0 |
|
|
|||||||||
Примеры |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1. lim |
ln 3 x |
lim |
1/ x |
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2. lim |
x3 |
lim |
3 x2 |
|
lim |
6 x |
lim |
6 |
|
|
0 ◄ |
|
|||||||||
|
|
4 e2 x |
|
|
|
|
|
||||||||||||||
x e2 x |
x 2 e2 x |
x |
|
x 8e2 x |
|
|
|
||||||||||||||
33.Формула Тейлора
33.1. Формула Тейлора для многочленов |
|
|
|
|
|||||
Разложим многочлен |
|
-й степени |
|
|
|
|
|
|
|
P (x) a xn a |
xn 1 |
a |
xn 2 |
... a x a |
, |
a 0 |
|||
n |
n |
n 1 |
|
n 2 |
|
1 |
0 |
|
n |
по степеням x x0 , где x0 |
- некоторое фиксированное число: |
|
|||||||
