
Электротехника Ч1
.pdf
61
мент t=0, k T/2) до 2RI2 (в моменты (2k-1) T/4), где Т=2π/ω - период тока.
Среднее за период значение мощности обозначают Р и называют ак-
тивной мощностью, причем
|
1 |
T |
|
|
P = |
∫ PR (t)dt = R I 2 . |
(5.13) |
||
T |
||||
|
0 |
|
||
|
|
|
Обратимся к векторной диаграмме рис. 5.1. Учтем, что падение напряжения на резистивном элементе цепи рис. 4.1 – UR = R·I = Uа·cosφ. С учетом правой части равенства (5.6) перепишем (5.12) в виде:
pR (t) = U I cosϕ − U I cosϕ cos 2ωt . |
(5.14) |
Первое слагаемое в правой части (5.14) полностью соответствует (5.13), т.е. определяет активную мощность цепи:
|
|
|
|
|
P = R I 2 = U I cosϕ [Вт]. |
(5.15) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выражение (5.15) используется на практике намного чаще, так как определяет зависимость активной мощности от сдвига фаз между действующими значениями тока и напряжения цепи. В силу этого коэффициент cos ϕ
называют коэффициентом мощности и обозначают λ:
λ = cosϕ . |
(5.16) |
62
Продолжим анализ слагаемых в выражении для мгновенной мощности цепи – (5.11). В нем третье и четвертое слагаемые определяют мощность, выделяемую на реактивных элементах:
– индуктивности:
pL (t) = X L I 2 sin 2ωt |
(5.17) |
– емкости: |
|
pC (t) = X c I 2 sin 2ωt . |
(5.18) |
Каждое из этих слагаемых изменяется с удвоенной (относительно тока) частотой, но они имеют взаимно противоположные фазы (рис. 5.3). Так как постоянная составляющая в (5.17) и (5.18) отсутствует, то среднее значение каждого из них равно нулю. Однако сумма pL(t) и pC(t) отлична от нуля и определяет мгновенную мощность реактивных элементов (участков) цепи – pr(t).
Определим эту мощность:
p |
(t) = p |
L |
(t) + p |
C |
(t) = ( X |
L |
− X |
C |
) I 2 sin 2ωt = X |
r |
I 2 |
sin 2ωt . (5.19) |
r |
|
|
|
|
|
|
|
|||||
Применим к (5.19) выражение (5.7), тогда |
|
|
|
|||||||||
|
|
|
|
|
pr (t) = U I sin ϕ sin 2ωt . |
|
|
(5.20) |
||||
Коэффициент |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
U I sinϕ = Q [вар] |
|
|
(5.21) |
||||
называется реактивной мощностью, обозначается Q и измеряется в вольт-
амперах реактивных [вар].
Теперь общее выражение для мгновенной мощности всей цепи (рис.4.1) можно записать в виде
p(t) = U I cosϕ − U I cosϕ cos 2ωt + U I sinϕ sin 2ωt . |
(5.22) |
Второе и третье слагаемые в (5.22) свернем как косинус суммы двух аргументов –cos(2ωt+φ). Тогда выражение (5.22) приходит к виду
p(t) = U I cosϕ − U I cos(2ωt + ϕ ) . |
(5.23) |
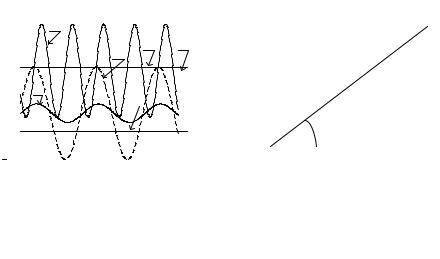
63
Таким образом, мгновенная мощность цепи содержит постоянную и переменную составляющие. Переменная составляющая мгновенной мощности изменяется относительно постоянной с удвоенной частотой (рис. 5.4). Графики рис. 5.4 иллюстрируют фазовые соотношения между мгновенными значениями тока i(t), напряжения u(t) и мощности p(t). Амплитудное значение переменной составляющей в (5.23) обозначают S и называют полной мощностью цепи:
|
|
|
|
S = U I [ВА]. |
(5.24) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полная мощность в cosφ раз превышает постоянную составляющую (активную мощность). Поэтому график мгновенной мощности заходит в область отрицательных значений. Величина области отрицательных значений определяется коэффициентом мощности. Физически эта область определяет моменты времени, в которые цепь возвращает энергию источнику.
Следует учитывать тот факт, что полная и активная мощности являются арифметическими величинами, а реактивная мощность – величина алгебраическая. Когда индуктивное сопротивление цепи по абсолютной величине больше емкостного, разность фаз между током и напряжением положительна – φ > 0. Поэтому Q = U · I · sinφ >0.
Когда большей оказывается величина емкостного сопротивления, реактивная мощность становится отрицательной. Именно такой вариант соот-

64
ношения реактивных сопротивлений в цепи рис. 4.1 отражают графики рис. 5.4. Они рассчитаны для следующих значений величин: i(t) = 2 · sin(314 · t), R = 5 Ом, L = 0,5 Гн, С = 20 мкФ.
Если умножить все стороны треугольника сопротивлений (рис.4.2) на I 2 , то получим треугольник мощностей (рис.5.5). В этом треугольнике гипотенуза эквивалентна полной мощности – S, прилежащей к острому углу катет – активной мощности Р, а противолежащий – реактивной мощности Q. Угол φ определяется сдвигом фаз между током и напряжением цепи и задает значение коэффициента мощности. Для треугольника очевидны соотношения:
S = P2 + Q2 , |
(5.25) |
P = U I cosϕ = S cosϕ,
Q = S sin ϕ ,
|
P |
(5.26) |
|
cosϕ = |
= λ. |
||
S |
|||
|
|
Полная мощность S – это теоретически достижимая, расчетная мощность, По значению S производятся расчеты сечения проводов, изоляция, параметры приемников электрической энергии. Из-за сдвига фаз φ мощность полностью не реализуется. Поэтому cosφ и получил название коэффициента мощности. Значение коэффициента мощности всегда стремятся обеспечить достаточно большим.
3. ВЫРАЖЕНИЕ МОЩНОСТИ В КОМПЛЕКСНОЙ ФОРМЕ
Широкое применение комплексного представления тока и напряжения в процессе анализа электрических цепей предполагает найти комплексное представление для активной, реактивной и полной мощности. На первый взгляд, эта задача не должна вызывать затруднений. Достаточно в выраже-
65
ние для мощности подставить комплексные значения тока и напряжения. Посмотрим, так ли это?
& |
jϕi |
и напряжение |
Пусть заданы комплексные ток Im = Im е |
|
U&m = Um е jϕU . Тогда их произведение должно представлять комплексную форму полной мощности цепи:
& |
& |
|
|
|
Um |
Im |
= U I e j(ϕu +ϕi ) = U I cos(ϕu + ϕi ) + j U I sin(ϕu + ϕi ). |
2 |
|
||
|
|
||
Правая часть полученного выражения должна определять активную (действительную часть) и реактивную (мнимую часть) мощности. Но слагаемые правой части не соответствуют выражениям (5.15) и (5.21), так как в последних сдвиг фаз определяется разностью
φ = φ1 – φ2.
Чтобы устранить такое несоответствие, пользуются искусственным приемом. Под комплексным изображением полной мощности понимают
произведение комплексного напряжения на комплексно-сопряженный ток.
Напомним, что два комплексных числа I& и I&* называются взаимно сопряженными, если их действительные части равны, а мнимые отличаются только знаком. Например,
I& = i′ + ji′′ = I (cosϕ + j sinϕ ) = I e jϕ ;
I&* = i′ − ji′′ = I (cosϕ − j sinϕ ) = I e− jϕ .
При таком определении комплексная мощность цепи определится таким выражением:
~ |
|
& |
|
&* |
|
j(ϕ |
|
−ϕ |
) |
|
||
|
U |
m |
I |
m |
|
|
|
|||||
S |
= |
|
|
|
= U I e |
|
u |
i |
|
. |
||
|
|
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||
Применим действующие значения тока и напряжения. Тогда выражение для комплексной мощности принимает вид:
66
~ |
& &* |
= U I cosϕ + j U |
I sinϕ = |
S |
= U I |
||
= S cosϕ + jS sinϕ = P + jQ. |
(5.27) |
||
|
|||
Знак «тильда» означает комплекс полной мощности, составленный при участии сопряженного комплекса тока. Действительная часть комплексной мощности есть активная мощность, а мнимая часть - реактивная мощность. Модуль комплексного представления определяет полную мощность.
Рассмотрим пример.
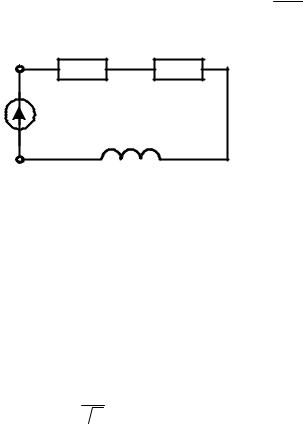
Пусть в схеме рис. 5.6 заданы Э.Д.С. – e(t) = 141·sin(ω·t) [B] и пара-
метры элементов: R1=3 Ом; R2=2 Ом; L=0,0095 Гн; ω = 314 Рад .
с
R1 R2
e(t)
L
Рис. 5.6. Схема с последовательным соединением элементов
Определить активную, реактивную и полную мощности цепи.
Решение:
1. Определяем значение действующего напряжения на входе всей схемы в комплексной форме:
U& = Em = 100[B].  2
2
2. Определяем сопротивление цепи в комплексной алгебраической форме:
Z = R1 + R2 + jωL = 3 + 2 + j314 0,0095 = 5 + j2,983.

67
3. Переходим к показательной форме комплексного сопротивления. Для этого:
а) находим модуль
Z = 52 + (2,983)2 |
≈ 5,82, |
||
б) фазу |
|
|
|
ϕ = arctg |
2,983 |
= 31o, |
|
|
|||
5 |
|
|
|
в) общее выражение |
|
|
|
|
|
|
o |
Z = 5,82 exp |
j31 . |
||
|
|
|
|
4. Вычисляем значение действующего тока в показательной комплексной форме:
& |
|
& |
|
100 |
|
o |
||
|
U |
|
||||||
I |
= |
|
|
= |
|
= 17,2 exp |
− j31 |
. |
|
|
5,82 e j310 |
||||||
|
|
|
Z |
|
|
|
|
|
Сопряженный комплекс тока:
&* |
|
o |
|
I |
= 17,2 exp |
j31 |
|
|
|
|
. |
5. Переходим к определению мощности в комплексной форме:
~ |
& &* |
|
o |
o |
o |
|
S |
= U I |
= 100 17,2 exp |
j31 |
|
= 1720 cos31 |
+ j1720sin 31 . |
|
|
|
|
|
|
|
Отсюда
P = 1475(Вт); Q = 886(вар); S = 1720(ВА).
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
5.1.Что характеризует мгновенная мощность цепи?
5.2.Приведите соотношения для активной мощности цепи. Может ли активная мощность принимать отрицательные значения?

68
5.3.Приведите соотношения для реактивной мощности цепи. Какой физический процесс характеризует реактивная мощность? Может ли она принимать отрицательные значения?
5.4.Что определяет коэффициент мощности цепи? Почему его стремятся повы-
сить?
5.5.Может ли мгновенная мощность цепи принимать отрицательные значения?
5.6.Приведите соотношения между полной, активной и реактивной мощностью
цепи.
5.7.Приведите комплексное изображение полной мощности.
5.8.Определите комплексное изображение полной мощности для цепи рис. 4.1, используя данные задач 4.6 и 4.7.
ЛЕКЦИЯ 6. ЧАСТОТНЫЕ СВОЙСТВА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ СИНУСОИДАЛЬНОГО ТОКА
Известно, что алгебраическая форма комплексного сопротивления Z имеет действительную R и мнимую X части:
Z = R + jX .
Значения действительной и мнимой частей определяются составом и топологией схемы. Для схемы с последовательно включенными элементами R, L, и С реактивное сопротивление определяется выражением:
X = ωL − 1 .
ωC
Очевидно, что значение слагаемых реактивного сопротивления зависит от частоты ω. На малых частотах емкостная составляющая имеет большое значение, а индуктивная – малое. Поэтому реактивное сопротивление схемы Х принимает емкостной характер. На больших частотах Х принимает индуктивный характер.

69
Существует такая частота ω0, на которой
1
ω0 L = ω0C .
На этой частоте реактивное сопротивление равно нулю, а комплексное сопротивление цепи становится активным. Такой режим выделяют особо и называют резонансным. Под резонансным режимом работы электрической цепи понимают режим, при котором ее сопротивление является чисто ак-
тивным.
Различают две разновидности резонансных режимов: резонанс токов и резонанс напряжений. Рассмотрим каждый из режимов.
1. РЕЗОНАНС ТОКОВ
Резонанс токов возникает в цепи с параллельным включением элементов (рис.6.1). Такая цепь содержит два сложных потенциальных узла, а все элементы находятся под одним и тем же напряжением.
u(t) = Um sinωt . |
(6.1) |
Для любого из узлов - 1 или 1’ справедлив первый закон Кирхгофа:
|
|
i(t) = iR (t) + iL (t) + iC (t). |
|
(6.2) |
|||||||
Применяя к (6.2) выражения (1.7) и (1.12), приведем его к виду |
|
||||||||||
|
|
|
u(t) |
|
1 |
t |
du(t) |
|
|
||
|
i(t) = |
|
+ |
|
|
∫u(t)dt + C |
|
. |
(6.3) |
||
R |
|
L |
dt |
||||||||
|
|
|
|
|
0 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Подставим в (6.3) вместо u(t) его значение из (6.1) и решим его: |
|
||||||||||
i(t) = |
Um |
sinωt − |
Um |
cosωt + UmωC cosωt. |
(6.4) |
||||||
|
|
||||||||||
|
R |
|
|
|
ωL |
|
|
|
|||
Векторная диаграмма, построенная по (6.4) приведена на рис. 6.2. В качестве исходного в ней принят общий для всех элементов цепи вектор на-
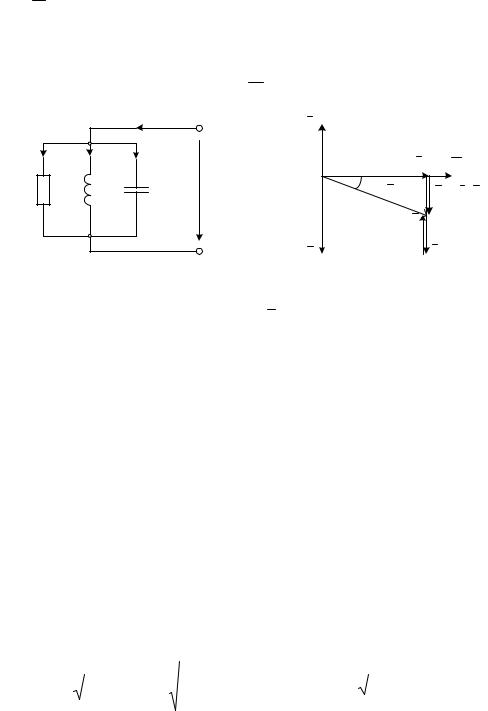
70
пряжения U . С этим вектором совпадает по направлению вектор тока через резистор. Его величина по модулю равна
I R = UR .
u(t)
Вектор тока через индуктивность – I L отстает от вектора напряжения,
а вектор тока через емкость – |
I |
c опережает его на 90°. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Проведем последовательное сложение векторов |
I |
a = |
I |
R |
I |
L |
и |
I |
C . Ре- |
||||||||||||||||||||||||||||||||||||||||
зультатом сложения является значение вектора тока – |
|
|
|
. Он сдвинут по фазе |
|||||||||||||||||||||||||||||||||||||||||||||
I |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
на угол ϕ. Сумма векторов |
|
I L и I C |
|||||||||||||||||||||||||||||
относительно вектора напряжения U |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
дает значение вектора реактивного тока – |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
I |
r . Модуль этого вектора опреде- |
|||||||||||||||||||||||||||||||||||||||||||||||
ляется выражением: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
Ir = UωC − |
|
U |
= U ωC − |
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
(6.5) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ωL |
|
|
|
|
|
|
|
|
|
|
ωL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Векторы |
I |
a , |
I |
и |
I |
r образуют треугольник токов. Для этого треуголь- |
|||||||||||||||||||||||||||||||||||||||||||
ника справедливы выражения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
+ ωC − |
1 |
|
|
2 = U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
I = Ia2 + Ir2 = U |
|
|
G2 + B2 . |
(6.6) |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
ωL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωC |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
Ir |
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
ϕ = аrctg |
|
= arctg |
ωL |
|
= arctg |
|
. |
|
|
|
|
|
(6.7) |
|||||||||||||||||||||||||||||||||
|
|
|
Ia |
|
|
1 |
|
|
|
|
|
|
|
G |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
R
