
Парыгина СА_Математическая статистика-SPSS
.PDFДля реализации МГК с помощью пакета SPSS необходимо:
1.Выбрать следующие команды меню и подменю: Анализ → Снижение размерности → Факторный анализ.
2.Перенести все исходные переменные в окно Переменные.
3.Использование кнопки Извлечение позволяет: уточнить сам метод уменьшения количества исходных признаков (МГК или ка- кой-либо другой), вывести на экран график собственных значений, выделить собственные значения по величине и количеству.
4.Кнопка Вращение позволяет выбрать метод вращения матрицы факторных нагрузок главных компонент. В ряде случаев это позволяет упростить изначально сложную для интерпретации матрицу факторных нагрузок. Удобно использовать метод Варимакс, также нужно установить галочку Повернутое решение, чтобы вывести на экран матрицу факторных нагрузок после вращения.
5.Установление в окне кнопки Значения факторов галочки Сохранить как переменные позволяет получить значения самих главных компонент в качестве дополнительных переменных на вкладке Данные. По умолчанию используется регрессионный метод.
6.Использование кнопки Параметры позволяет определить формат вывода весовых коэффициентов с помощью галочки Не выводить коэффициенты с низкими значениями, при этом в строке Абсолютное значение меньше рекомендуется установить значения: 0,6; 0,5 или 0,4.
7.Запустить МГК, нажав кнопку Ок.
Рассмотрим, как решается задача выявления внутренних (латентных) характеристик с помощью метода главных компонент в SPSS на примере исследования особенностей сельскохозяйственной деятельности нескольких районов области [3]. Первичными переменными в данном случае являются результаты измерения следующих шести показателей:
1)количество удобрений, расходуемых на 1 га (переменная
количество_удобрений);
2)количество средств защиты растений, расходуемых на 1 га
(переменная средства_защиты);
3)урожайность с гектара (переменная урожайность);
31
4)число колесных тракторов на 100 га (переменная чис-
ло_тракторов);
5)число зерноуборочных комбайнов на 100 га (переменная
число_комбайнов);
6)число орудий поверхностной обработки почвы на 100 га
(переменная число_орудий).
Процедура ввода исходной статистической информации в редактор данных SPSS была рассмотрена ранее (см. лабораторную работу 1), поэтому перейдем к анализу результатов МГК.
Основные результаты МГК в пакете SPSS представлены в виде трех таблиц. Заметим, что по умолчанию корреляционная матрица исходных переменных в отчете SPSS не приводится, для ее вывода нужно использовать кнопку Извлечение.
Первая таблица отчета, которая носит название «Общности», показывает, какая часть дисперсии каждой из включенных в анализ переменных описывается общими факторами, т.е. теми ненаблюдаемыми характеристиками, которые мы ищем (табл. 5.1).
|
Общности |
Таблица 5.1 |
||
|
|
|
||
|
|
|
|
|
Общности |
|
Начальные |
Извлеченные |
|
Количество_удобрений |
|
1,000 |
0,948 |
|
Средства_защиты |
|
1,000 |
0,877 |
|
Урожайность |
|
1,000 |
0,963 |
|
Число_тракторов |
|
1,000 |
0,862 |
|
Число_комбайнов |
|
1,000 |
0,926 |
|
Число_орудий |
|
1,000 |
0,884 |
|
Как видно из табл. 5.1, все рассматриваемые переменные достаточно хорошо описываются построенной факторной моделью, так как соответствующие дисперсии изменяются в пределах от 96,3 %
до 86,2 %.
Следующая таблица «Полная объясненная дисперсия» содержит информацию о том, какой вклад в общую дисперсию вносит каждая полученная компонента. А именно, в таблице содержатся следующие характеристики компонент, выявленных с помощью МГК:
32
собственные значения корреляционной матрицы исходных переменных, расположенные в порядке убывания: 1 2 ... p ;
вклад (%) в общую дисперсию каждой из компонент или ве-
личина pr 100%, r 1,2,..., p ;
кумулятивный (накопленный) вклад главных компонент или
величина r q |
r 100 %, где q – число используемых главных |
r 1 |
p |
компонент, т.е. q p (см. табл. 5.2).
|
|
Полная объясненная дисперсия |
Таблица 5.2 |
|||||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
Начальные собственные |
Суммы квадратов нагрузок |
||||||
Компо- |
|
значения |
|
|
извлечения |
|
||
нента |
Итого |
% дис- |
|
Кумуля- |
Итого |
% дис- |
Кумуля- |
|
|
персии |
|
тивный % |
персии |
тивный % |
|
||
1 |
3,061 |
51,013 |
|
51,013 |
3,061 |
51,013 |
51,013 |
|
2 |
1,299 |
21,651 |
|
72,664 |
1,299 |
21,651 |
72,664 |
|
3 |
1,100 |
18,339 |
|
91,003 |
1,100 |
18,339 |
91,003 |
|
4 |
0,337 |
5,622 |
|
96,626 |
|
|
|
|
5 |
0,127 |
2,113 |
|
98,739 |
|
|
|
|
6 |
0,076 |
1,261 |
|
100,00 |
|
|
|
|
Данную таблицу можно условно разделить на две части: слева описываются все p выявленных в ходе факторного анализа компо-
нент, а справа – только q главных компонент. Обращаясь к табл. 5.2, мы видим, что из p 6 возможных компонент отобрано q 3 главных компоненты, которые вносят наибольший вклад в
общую дисперсию (примерно 51, 22 и 18 %, соответственно) и в целом описывают r 91 % общей дисперсии. В данном случае для
определения количества главных компонент, равного трем, был использован принятый в SPSS по умолчанию критерий Кайзера, который рекомендует отбирать столько главных компонент, сколько
33
найдено собственных чисел корреляционной матрицы, больших единицы.
Однако это не единственный подход к решению важнейшей для МГК проблемы отбора такого количества главных компонент, которое позволит и сократить число анализируемых переменных, и описать как можно больший процент объясненной дисперсии.
Второй подход основан на самостоятельном определении числа главных компонент в соответствии с заданной величиной объясняемой ими дисперсии r . Так, из таблицы 5.2. следует, что если бы
построенная факторная модель должна была объяснять не менееr 70 % общей дисперсии, то достаточно было бы взять первые
две главных компоненты. Минусом данного подхода является то, что не существует четких рекомендаций по выбору величины объясняемой дисперсии r . Конечно, чем больше этот процент, тем
лучше, но нужно помнить и о главной задаче МГК – уменьшении числа исходных переменных. В рамках данного подхода большую роль приобретают рекомендации, приводимые в литературе или при проведении предыдущих исследований, кроме того, существуют некоторые характерные для определенных наук значения. Например, в социологии часто встречаются факторные модели, объясняющие 60 – 75 % общей дисперсии.
Третий подход базируется на так называемом «методе каменной осыпи». Суть метода: строится график, в котором по оси абсцисс откладываются номера главных компонент, а по оси ординат – значения собственных чисел для каждой из них. Так как собственные числа в МГК вычисляются в порядке убывания, то и график будет убывающим. При этом значимые компоненты образуют крутой склон, а малозначимые – пологий спуск, напоминающий каменную осыпь или мелкий щебень. Между этими частями графика обычно наблюдается резкое понижение, выше которого и расположены главные компоненты. График, соответствующий данным табл. 5.2, изображен на рис. 5.1. Анализируя его, можно заметить, что крутой склон образуют первые три главных компоненты, далее – резкое понижение и щебень, который образуют компоненты с 4-й по 6-ю.
34
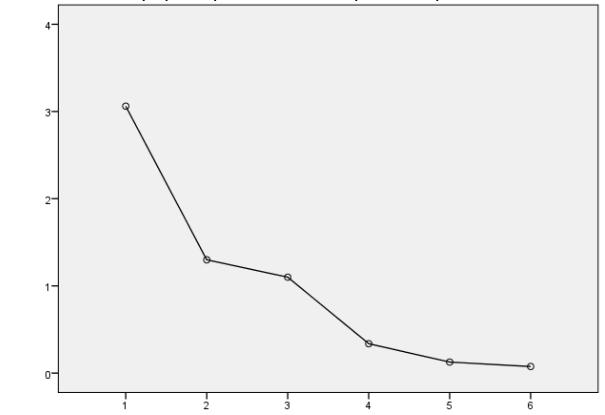
Собственное значение
Номер компоненты
Рис. 5.1. График нормализованного простого стресса
Таким образом, данный подход, как и критерий Кайзера, рекомендует ограничиться 3-мя главными компонентами.
Следующая таблица отчета «Матрица компонент» содержит начальные значения факторных нагрузок ajr , отражающие корреля-
ционную зависимость между главными компонентами и первичными переменными до вращения факторов (см. табл. 5.3).
|
Матрица компонент |
Таблица 5.3 |
|||
|
|
|
|||
|
|
|
|
|
|
|
|
|
Компонента |
|
|
|
|
1 |
2 |
3 |
|
Количество_удобрений |
|
0,670 |
|
0,707 |
|
Средства_защиты |
|
0,806 |
|
|
|
Урожайность |
|
|
0,791 |
0,449 |
|
Число_тракторов |
|
0,649 |
0,454 |
-0,484 |
|
Число_комбайнов |
|
0,925 |
|
|
|
Число_орудий |
|
0,741 |
0,570 |
|
|
|
|
|
|
35 |
|

Поскольку более удобную матрицу факторных нагрузок дают методы вращения факторов, рассмотрим аналогичную матрицу, но уже после вращения, она носит название «Матрица повернутых компонент» (см. табл. 5.4).
Матрица повернутых компонент |
|
|
Таблица 5.4 |
||||||
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
Компонента |
|
|
|
|
|||
|
1 |
|
2 |
|
|
|
|
3 |
|
Количество_удобрений |
|
|
0,960 |
|
|
-0,485 |
|
||
Средства_защиты |
|
|
0,830 |
|
|
|
|
||
Урожайность |
|
|
|
|
|
|
|
0,980 |
|
Число_тракторов |
0,920 |
|
|
|
|
|
|
|
|
Число_комбайнов |
0,606 |
|
|
|
|
|
|
|
|
Число_орудий |
0,877 |
|
|
|
|
|
|
|
|
В табл. 5.3 и 5.4 установлено ограничение: |
|
ajr |
|
0,4. Мы ви- |
|||||
|
|
||||||||
дим, что в отличие от матрицы нагрузок до вращения (табл. 5.3), матрица после вращения (табл. 5.4) заметно удобнее, так как вклад исходных переменных в ту или иную главную компоненту выражен в ней более явно и однозначно, поэтому интерпретацию факторов сделать гораздо легче.
Итак, первая главная компонента F1 имеет сильную положительную связь с переменными «Число колесных тракторов», «Число зерноуборочных комбайнов» и «Число орудий поверхностной обработки почвы» на 100 га. Следовательно, она отвечает за работу сельскохозяйственной техники и ее можно интерпретировать как
«Уровень механизации сельскохозяйственных работ».
Вторая главная компонента F2 имеет сильную положительную связь с переменными «Количество удобрений, расходуемых на гектар» и «Количество средств защиты растений, расходуемых на гектар». Поэтому, ее можно интерпретировать как «Уровень химизации сельскохозяйственных работ».
И третья главная компонента F3 имеет сильную положительную связь с переменной «Урожайность с гектара» и слабую отрицатель-
36

ную связь с переменной «Количество удобрений, расходуемых на гектар». Следовательно, она характеризует высокую урожайность при минимальных дозах химикатов и наоборот, поэтому ее можно интерпретировать как «Уровень развития органического земледелия».
Таким образом, мы выявили три основных характеристики сельскохозяйственной деятельности в исследуемых районах.
Практическая часть
Задание 1
Предположим, что проводится исследование жизненных стратегий испытуемых, т.е. что важно для достижения успеха в жизни. В соответствующем опроснике предлагались следующие варианты ответов (первичные переменные):
1.Происходить из материально обеспеченной семьи
2.Иметь хорошее образование
3.Иметь амбиции для продвижения по жизни
4.Иметь высокопоставленных родителей
5.Иметь связи в криминальном мире
6.Иметь везение, счастливый случай
7.Иметь природные задатки
8.Много работать
9.Иметь необходимые знакомства, связи
10.Иметь нравственные убеждения
11.Проживать в определенном регионе
12.Важно, каков твой пол
Все испытуемые определили для себя и выставили оценки по степени важности каждого из перечисленных первичных признаков, данные представлены в табл. 1, 2 прил. 4. Требуется: с помощью МГК выявить латентные признаки (характеризующие жизненные стратегии испытуемых) на основе первичных факторов, извлекая оптимальное число главных компонент.
37

ПРИЛОЖЕНИЯ
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
П р и л о ж е н и е 1 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Номер |
|
|
|
|
|
|
|
|
Уровни фактора F |
|
|
|
|
|
|
|
||||||
|
испытания |
|
|
F1 |
|
|
|
|
F2 |
|
|
|
F3 |
|
|
|
F4 |
|
|
|
|||
|
|
1 |
|
|
a + 1 |
|
|
a + 21 |
|
|
|
b + 7 |
|
|
A + 4 |
|
|
||||||
|
|
2 |
|
|
b + 2 |
|
|
b + 16 |
|
|
|
c + 10 |
|
|
b + 12 |
|
|
||||||
|
|
3 |
|
|
с + 3 |
|
|
|
c + 17 |
|
|
|
b + 14 |
|
|
2 a- 7 |
|
|
|||||
|
|
4 |
|
|
c + 9 |
|
|
|
2a - 4 |
|
|
|
c + 11 |
|
|
c + 14 |
|
|
|||||
|
|
5 |
|
|
2а - 3 |
|
|
|
2a - 3 |
|
|
|
2a + 9 |
|
|
2a - 5 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
По- |
|
|
|
|
|
|
|
Номера вариантов |
|
|
|
|
|
|
|
|||||||
стоян- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
3 |
4 |
5 |
|
6 |
|
7 |
|
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|||||
|
ные |
|
|
|
|
||||||||||||||||||
|
α |
0,01 |
0,05 |
0,01 |
0,05 |
0,01 |
0,05 |
|
0,01 |
|
0,05 |
0,01 |
0,05 |
0,01 |
0,05 |
0,01 |
0,05 |
0,01 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
a |
35 |
36 |
34 |
37 |
33 |
|
38 |
|
32 |
|
39 |
31 |
40 |
30 |
41 |
29 |
28 |
42 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
b |
45 |
46 |
44 |
47 |
43 |
|
48 |
|
42 |
|
49 |
41 |
50 |
40 |
51 |
39 |
38 |
52 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
c |
47 |
48 |
46 |
49 |
45 |
|
50 |
|
44 |
|
51 |
43 |
52 |
42 |
53 |
41 |
40 |
54 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
38
П р и л о ж е н и е 2
Таблица 1
|
Номер |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 |
|
|
2 |
|
3 |
|
4 |
|
|
|
5 |
|
6 |
|
|
7 |
|
|
8 |
|
|
|||||||||||||||
|
испытуемого |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
X |
|
Y |
|
X |
Y |
X |
Y |
|
X |
Y |
|
X |
|
Y |
|
X |
Y |
X |
|
Y |
X |
Y |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
1 |
1 |
|
2 |
0 |
|
9 |
|
2 |
|
0 |
0,5 |
|
|
4 |
1 |
|
2 |
|
1 |
|
6 |
|
2 |
|
0 |
|
6 |
|
6 |
|
|||||||
|
2 |
2 |
|
2 |
1 |
|
8 |
|
3 |
|
1 |
1 |
|
|
3 |
2 |
|
3 |
|
1 |
|
7 |
|
2 |
|
1 |
|
7 |
|
5 |
|
|||||||
|
3 |
3 |
|
2 |
1 |
|
9 |
|
5 |
|
2 |
1,5 |
|
|
2 |
3 |
|
2 |
|
2 |
|
6 |
|
3 |
|
2 |
|
7 |
|
7 |
|
|||||||
|
4 |
4 |
|
4 |
2 |
|
7 |
|
5 |
|
3 |
2 |
|
|
2 |
4 |
|
3 |
|
3 |
|
5 |
|
3,5 |
|
4 |
|
8 |
|
4 |
|
|||||||
|
5 |
5 |
|
6 |
2 |
|
8 |
|
7 |
|
4 |
2,5 |
|
|
2 |
5 |
|
4 |
|
4 |
|
4,5 |
|
4 |
|
3 |
|
8 |
|
6 |
|
|||||||
|
6 |
7 |
|
8 |
3 |
|
5 |
|
8 |
|
5 |
3 |
|
|
1,5 |
7 |
|
4 |
|
5 |
|
4 |
|
5 |
|
4 |
|
8 |
|
8 |
|
|||||||
|
7 |
8 |
|
9 |
4 |
|
5 |
|
8 |
|
6 |
3,5 |
|
|
2 |
8 |
|
4 |
|
5,5 |
|
3 |
|
5 |
|
5 |
|
9 |
|
7 |
|
|||||||
|
8 |
9 |
|
10 |
4 |
|
4 |
|
9 |
|
6 |
4 |
|
|
1 |
9 |
|
5 |
|
6 |
|
3 |
|
5 |
|
6 |
|
10 |
|
5 |
|
|||||||
|
9 |
10 |
|
11 |
5 |
|
3 |
|
9 |
|
7 |
5 |
|
|
1 |
10 |
|
5 |
|
7 |
|
2 |
|
6 |
|
7 |
|
10 |
|
7 |
|
|||||||
|
10 |
11 |
|
9 |
5 |
|
2 |
|
10 |
7 |
5 |
|
|
0,5 |
11 |
|
4,5 |
|
7,5 |
|
1,5 |
|
6 |
|
8 |
|
11 |
|
4 |
|
||||||||
|
11 |
12 |
|
12 |
6 |
|
1 |
|
11 |
8 |
5,5 |
|
|
0,5 |
12 |
|
4 |
|
8 |
|
1,5 |
|
7 |
|
8 |
|
11 |
|
6 |
|
||||||||
|
12 |
13 |
|
12 |
7 |
|
0,5 |
12 |
9 |
6 |
|
|
0 |
13 |
|
6 |
|
9 |
|
1 |
|
8 |
|
11 |
|
12 |
|
7 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1 (продолжение) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Номер |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
9 |
|
|
10 |
|
|
11 |
|
|
12 |
|
|
|
13 |
|
14 |
|
|
|
15 |
|
|
|
||||||||||||||
|
испытуемого |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
X |
Y |
X |
Y |
X |
Y |
X |
Y |
X |
Y |
X |
Y |
X |
Y |
||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
|
1 |
2 |
|
|
4 |
|
|
1 |
|
7 |
|
1 |
|
1 |
|
|
5 |
|
1 |
|
|
0 |
|
|
3 |
|
0 |
|
5 |
|
9 |
|
|
|
5 |
|
||
|
2 |
3 |
|
|
1 |
|
|
3 |
|
6 |
|
1 |
|
3 |
|
|
5 |
|
2 |
|
|
1 |
|
|
2 |
|
1 |
|
4 |
|
10 |
|
|
6 |
|
|||
|
3 |
3 |
|
|
3 |
|
|
4 |
|
7 |
|
2 |
|
1 |
|
|
6 |
|
3 |
|
|
1 |
|
|
3 |
|
1 |
|
7 |
|
8 |
|
|
|
7 |
|
||
|
4 |
3 |
|
|
4 |
|
|
5 |
|
6 |
|
2 |
|
2 |
|
|
8 |
|
4 |
|
|
1 |
|
|
4 |
|
2 |
|
5 |
|
9 |
|
|
|
8 |
|
||
|
5 |
3 |
|
|
5 |
|
|
6 |
|
7 |
|
2 |
|
3 |
|
|
8 |
|
3 |
|
|
2 |
|
|
1 |
|
2 |
|
7 |
|
11 |
|
|
8 |
|
|||
|
6 |
4 |
|
|
2 |
|
|
7 |
|
5 |
|
3 |
|
5 |
|
|
9 |
|
3 |
|
|
2 |
|
|
3 |
|
3 |
|
7 |
|
8 |
|
|
|
9 |
|
||
|
7 |
4 |
|
|
3 |
|
|
8 |
|
6 |
|
4 |
|
1 |
|
|
10 |
|
4 |
|
|
3 |
|
|
2 |
|
3 |
|
9 |
|
7 |
|
|
|
9 |
|
||
|
8 |
4 |
|
|
4 |
|
|
9 |
|
4 |
|
4 |
|
5 |
|
|
10 |
|
3 |
|
|
4 |
|
|
0 |
|
4 |
|
10 |
|
9 |
|
|
|
13 |
|
||
|
9 |
5 |
|
|
2 |
|
|
10 |
|
3 |
|
5 |
|
3 |
|
|
11 |
|
3 |
|
|
4 |
|
|
2 |
|
4 |
|
13 |
|
10 |
|
|
10 |
|
|||
|
10 |
5 |
|
|
3 |
|
|
11 |
|
5 |
|
5 |
|
4 |
|
|
11 |
|
4 |
|
|
4 |
|
|
3 |
|
5 |
|
11 |
|
8 |
|
|
|
4 |
|
||
|
11 |
6 |
|
|
2 |
|
|
12 |
|
3 |
|
6 |
|
3 |
|
|
12 |
|
3 |
|
|
5 |
|
|
3 |
|
6 |
|
13 |
|
10 |
|
|
12 |
|
|||
|
12 |
6 |
|
|
4 |
|
|
13 |
|
4 |
|
7 |
|
4 |
|
|
12 |
|
4 |
|
|
6 |
|
|
0 |
|
7 |
|
14 |
|
11 |
|
|
11 |
|
|||
39

Таблица 2
|
Номер |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
|
|
|
2 |
|
|
3 |
|
|
4 |
|
5 |
|
|
6 |
|
|
|
|
|
7 |
|
|
|
|
8 |
|
||||||||||||
|
респондента |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
X |
|
Y |
|
X |
|
Y |
X |
|
|
Y |
X |
|
|
Y |
|
X |
|
|
Y |
|
X |
|
Y |
|
X |
|
Y |
|
X |
|
Y |
||||||||||
1 |
2 |
|
19 |
|
2 |
|
31 |
2 |
|
33 |
|
1 |
|
32 |
|
6 |
|
39 |
5 |
|
17 |
|
2 |
|
20 |
|
6 |
|
|
38 |
|
|||||||||||
2 |
1 |
|
22 |
|
6 |
|
28 |
3 |
|
36 |
|
3 |
|
29 |
|
8 |
|
35 |
8 |
|
22 |
|
4 |
|
30 |
|
8 |
|
|
39 |
|
|||||||||||
3 |
3 |
|
25 |
|
8 |
|
33 |
6 |
|
20 |
|
2 |
|
36 |
|
7 |
|
28 |
6 |
|
29 |
|
3 |
|
28 |
|
5 |
|
|
30 |
|
|||||||||||
4 |
4 |
|
24 |
|
7 |
|
25 |
8 |
|
18 |
|
4 |
|
31 |
|
5 |
|
24 |
3 |
|
36 |
|
1 |
|
33 |
|
7 |
|
|
25 |
|
|||||||||||
5 |
7 |
|
36 |
|
5 |
|
20 |
7 |
|
21 |
|
6 |
|
35 |
|
2 |
|
20 |
4 |
|
34 |
|
6 |
|
35 |
|
4 |
|
|
27 |
|
|||||||||||
6 |
5 |
|
37 |
|
3 |
|
18 |
4 |
|
25 |
|
5 |
|
38 |
|
4 |
|
22 |
1 |
|
40 |
|
5 |
|
36 |
|
3 |
|
|
28 |
|
|||||||||||
7 |
8 |
|
28 |
|
4 |
|
19 |
1 |
|
30 |
|
8 |
|
40 |
|
1 |
|
19 |
7 |
|
26 |
|
8 |
|
40 |
|
2 |
|
|
19 |
|
|||||||||||
8 |
6 |
|
35 |
|
1 |
|
22 |
5 |
|
40 |
|
7 |
|
39 |
|
3 |
|
21 |
2 |
|
18 |
|
7 |
|
39 |
|
1 |
|
|
17 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2 (продолжение) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Номер |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
9 |
|
|
10 |
|
|
11 |
|
|
|
12 |
|
|
|
13 |
|
|
|
|
14 |
|
|
15 |
|
||||||||||||||||
|
респондента |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
X |
|
Y |
|
X |
|
Y |
|
|
X |
|
Y |
|
|
X |
|
Y |
|
X |
|
Y |
|
X |
|
|
Y |
|
X |
|
|
Y |
|
||||||||
|
1 |
|
|
6 |
|
26 |
3 |
|
18 |
|
|
5 |
|
26 |
|
|
8 |
|
40 |
|
1 |
|
18 |
|
2 |
|
|
35 |
|
5 |
|
21 |
|
|||||||||
|
2 |
|
|
8 |
|
24 |
6 |
|
17 |
|
|
6 |
|
21 |
|
|
5 |
|
38 |
|
3 |
|
29 |
|
5 |
|
|
32 |
|
6 |
|
23 |
|
|||||||||
|
3 |
|
|
7 |
|
35 |
1 |
|
25 |
|
|
8 |
|
38 |
|
|
2 |
|
39 |
|
4 |
|
25 |
|
6 |
|
|
19 |
|
3 |
|
26 |
|
|||||||||
|
4 |
|
|
4 |
|
38 |
4 |
|
26 |
|
|
3 |
|
34 |
|
|
7 |
|
25 |
|
2 |
|
30 |
|
3 |
|
|
25 |
|
2 |
|
28 |
|
|||||||||
|
5 |
|
|
5 |
|
31 |
5 |
|
28 |
|
|
1 |
|
19 |
|
|
4 |
|
26 |
|
5 |
|
33 |
|
1 |
|
|
26 |
|
1 |
|
35 |
|
|||||||||
|
6 |
|
|
2 |
|
40 |
7 |
|
29 |
|
|
4 |
|
20 |
|
|
6 |
|
19 |
|
6 |
|
37 |
|
4 |
|
|
24 |
|
4 |
|
31 |
|
|||||||||
|
7 |
|
|
1 |
|
18 |
2 |
|
36 |
|
|
7 |
|
30 |
|
|
3 |
|
18 |
|
7 |
|
36 |
|
7 |
|
|
28 |
|
7 |
|
36 |
|
|||||||||
|
8 |
|
|
3 |
|
16 |
8 |
|
38 |
|
|
2 |
|
28 |
|
|
1 |
|
17 |
|
8 |
|
40 |
|
8 |
|
|
36 |
|
8 |
|
40 |
|
|||||||||
40
