
Парыгина СА_Математическая статистика-SPSS
.PDF4. В результирующей таблице приводятся сами значения выбранных коэффициентов корреляции, а также указывается их значимость.
Так как еще не все коэффициенты корреляции вычисляются на ЭВМ, в частности – с помощью пакета SPSS, и для лучшего понимания основ корреляционного анализа данных рассмотрим несколько примеров вычисления коэффициентов корреляции вручную.
Пример 1
Наблюдения за 9 подростками по переменным «Рост» (Х) и «Пол» (Y) приведены в табл. 3.1.
|
|
Таблица 3.1 |
|
|
|
|
|
Номер испытуемого |
Рост в см, Х |
Пол (1 – м., 0 – ж.), Y |
|
1 |
150 |
1 |
|
2 |
170 |
0 |
|
3 |
160 |
1 |
|
4 |
165 |
1 |
|
5 |
140 |
0 |
|
6 |
183 |
1 |
|
7 |
157 |
0 |
|
8 |
152 |
0 |
|
9 |
163 |
1 |
|
Определить, связаны ли линейной зависимостью переменные Х
иY.
Ре ш е н и е :
Так как переменная Х (рост) измерена в количественной шкале (шкала отношений), а переменная Y (пол) – в номинальнодихотомической шкале, то для определения линейной зависимости между данными переменными удобно использовать точечный бисериальный коэффициент корреляции rpb. Коэффициент rpb вычисляется по формуле
21
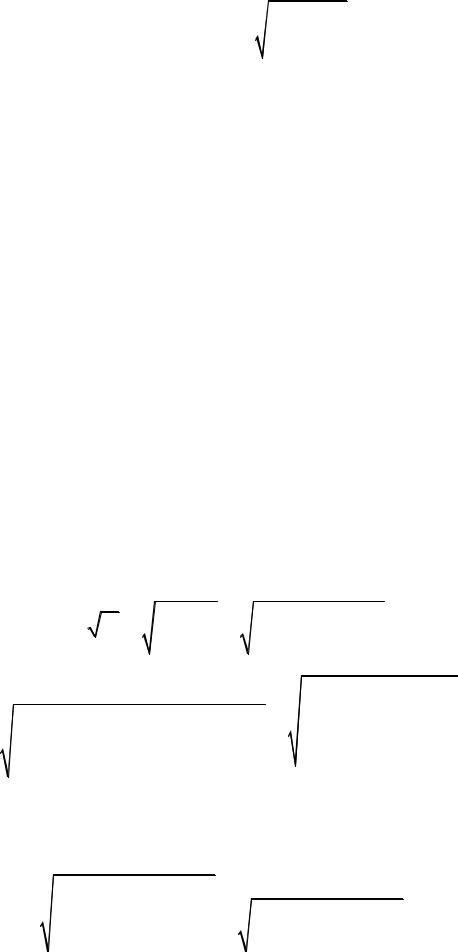
r |
x1 x0 |
|
n1 n0 |
, |
|
|
|||
pb |
sX |
|
n (n 1) |
|
|
|
|||
где x1 – среднее значение по переменной Х объектов, имеющих 1
по переменной Y;
x0 – среднее значение по переменной Х объектов, имеющих 0 по
переменной Y;
sX – исправленное среднеквадратическое отклонение всех значе-
ний переменной Х;
n1 – число объектов, имеющих 1 по переменной Y; n0 – число объектов, имеющих 0 по переменной Y; n – общий объем выборки, n = n1 + n0.
Проведем промежуточные вычисления.
n1 = 5, n0 = 4, n = 9.
x 150 160 165 183 163 |
821 164,2 ; |
|||||||||||||||
1 |
|
|
5 |
|
|
|
|
|
|
5 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x |
170 140 157 152 619 154,75. |
|||||||||||||||
0 |
|
|
4 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
n |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
x |
2 |
|
|
2 |
|
||||||
sX |
|
D |
n 1 |
s |
|
|
n 1 |
|
|
x |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Так как
n |
|
|
1 |
n |
2 |
|
1 |
n |
2 |
|
|
|||
|
|
|
|
xi |
|
|
|
|
xi |
|
|
|||
n 1 |
n |
2 |
||||||||||||
n |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
i 1 |
|
|
|
|
i 1 |
|
|
|
||
n |
xi |
821 619 1440, а n |
xi2 |
|||||||||||
i 1 |
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
n |
2 |
|
1 |
n |
2 |
|
xi |
|
xi |
|
|||
i 1 |
|
|
n |
i 1 |
|
. |
n1
231636, то
|
|
231636 |
1 |
1440 |
2 |
|
231636 |
230400 |
|
sX |
|
9 |
|
|
12,43. |
||||
8 |
|
|
|
|
8 |
||||
|
|
|
|
|
|
|
|
22

Вычисление величин x1, x0 , sX удобно проводить на ЭВМ с ис-
пользованием соответствующих команд пакета SPSS.
Подставим найденные значения в формулу для коэффициента
rpb.
r 164,2 154,75 |
|
5 4 |
|
9,45 |
20 |
0,76 0,53 0,4. |
|
pb |
12,43 |
|
9 8 |
|
12,43 |
72 |
|
|
|
|
|
||||
Таким образом, существует лишь слабая прямопропорциональная связь между ростом и полом у обследованных подростков.
Пример 2
12 учащихся ранжируются экспертом по их отношению к себе (переменная Х) и к другим учащимся (переменная Y). Исходные данные представлены в табл. 3.2.
|
|
Таблица 3.2 |
|
|
|
|
|
Номер учащегося |
Ранги по переменной Х |
Ранги по переменной Y |
|
1 |
2 |
6 |
|
2 |
8 |
5 |
|
3 |
12 |
10 |
|
4 |
3 |
7 |
|
5 |
1 |
3 |
|
6 |
6 |
4 |
|
7 |
7 |
9 |
|
8 |
10 |
8 |
|
9 |
4 |
1 |
|
10 |
9 |
11 |
|
11 |
11 |
12 |
|
12 |
5 |
2 |
|
Определить, связаны ли линейной зависимостью переменные Х и Y.
23
Р е ш е н и е :
Так как результатами измерения обеих переменных являются ранги соответствующих объектов, то измерения проведены в порядковой шкале. Значит, для измерения линейной связи между переменными Х и Y можно использовать как коэффициент корреляции Спирмена rs, так и коэффициент корреляции τ Кендалла.
а) Коэффициент корреляции Спирмена rs в случае различных рангов вычисляется по формуле:
6 n (xi yi )2
r 1 |
i 1 |
|
, |
|
|
||
s |
n (n2 |
1) |
|
|
|
где xi, yi – ранги i-го объекта по переменным Х и Y; n – объем всей выборки.
Проведем промежуточные вычисления.
n = 12, n |
(xi yi )2 16 9 4 16 4 4 4 4 9 4 1 9 84 , |
||||||||
i 1 |
|
|
|
|
|
|
|
|
|
тогда r 1 |
|
|
|
6 84 |
1 |
|
42 |
0,71. |
|
|
|
|
|
||||||
s |
|
|
12 |
(144 1) |
|
143 |
|||
|
|
|
|
||||||
Таким образом, значение коэффициента корреляции Спирмена свидетельствует о сильной прямопропорциональной связи между переменными Х и Y.
б) Коэффициент корреляции τ Кендалла в случае различных рангов может быть вычислен по формуле:
|
4P |
1, |
|
n(n 1) |
|||
|
|
где Р – это общее число совпадений, n – объем всей выборки. Составим вспомогательную табл. 3.3 для нахождения числа сов-
падений. В соответствии с правилом нахождения совпадений ранги по переменной Х в табл. 3.3 располагаются в порядке возрастания, а
24

номера объектов и ранги по переменной Y приписываются соответственно.
|
|
|
Таблица 3.3 |
|
|
Соответствующие |
|
Номер учащегося |
Упорядоченные |
Совпадения |
|
|
ранги по Х |
ранги по Y |
|
5 |
1 |
3 |
9 |
1 |
2 |
6 |
6 |
4 |
3 |
7 |
5 |
9 |
4 |
1 |
8 |
12 |
5 |
2 |
7 |
6 |
6 |
4 |
6 |
7 |
7 |
9 |
3 |
2 |
8 |
5 |
4 |
10 |
9 |
11 |
1 |
8 |
10 |
8 |
2 |
11 |
11 |
12 |
0 |
3 |
12 |
10 |
0 |
Сумма |
– |
– |
Р = 51 |
Сделаем подстановку в расчетную формулу
|
|
|
4 51 |
1 |
204 |
1 1,55 1 0,55. |
|
12 |
(12 1) |
132 |
|||||
|
|
|
|||||
Таким образом, значение коэффициента корреляции Кендалла свидетельствует о слабой положительной связи между переменными Х и Y. Так как коэффициент корреляции τ Кендалла считается более точным, то можно сказать, что между переменными, соответствующими отношению учащихся к себе и к другим учащимся, наблюдается лишь слабая прямопропорциональная связь.
25
Практическая часть
Задание 1
Исследователь изучает связь между временем, которое тратят испытуемые на просмотр телевизора (в часах) (переменная Х) и количеством хронических заболеваний, диагностированных у них (переменная Y). Результаты 12 испытуемых представлены в табл. 1 Приложения 2. По экспериментальным данным:
1.Построить диаграмму рассеяния.
2.Вычислить коэффициент корреляции Пирсона с помощью пакета SPSS.
3.Сделать вывод относительно типа линейной связи между переменными X и Y и обосновать его.
Задание 2
Исследователь изучает связь успешности рыночной деятельности бизнес-элиты с их уровнем самооценки (в баллах). Показатель успешности бизнесменов определяется путем ранжирования их по среднему уровню доходов (переменная Х), показатель уровня самооценки определяется с помощью соответствующего тестирования (переменная Y). Результаты 8 учащихся представлены в табл. 2 Приложения 2, причем по переменной Х ранжирование уже произведено. По экспериментальным данным определить:
1.Ранговые значения переменной Y.
2.Коэффициенты ранговой корреляции Спирмена и τ Кендалла
–двумя способами: вручную и с помощью пакета SPSS.
3.Сделать вывод относительно типа линейной связи между переменными X и Y и обосновать его.
Задание 3
Определить меру связи между признаками Х и Y с помощью соответствующего коэффициента корреляции и обосновать свой выбор:
26
1.Признак Х характеризует семейное положение респондента (женат – 1; холост – 0), а признак Y характеризует образование респондента (высшее образование – 1; нет высшего образования – 0). Данные приведены в табл. 3 Приложения 2.
2.Признак Х характеризует избирательную активность испытуемого (голосовал на последних выборах – 1; не голосовал – 0); а признак Y характеризует время (в мин.), затрачиваемое респондентом на просмотр предвыборных передач. Данные приведены в табл. 4 Приложения 2.
27
Лабораторная работа 4
Реализация методов кластерного анализа с помощью электронного пакета SPSS
Теоретическая часть
Электронный пакет SPSS предоставляет широкие возможности для статистической обработки данных, в том числе он позволяет проводить классификацию объектов исследования на группы (классы), идентичные (или почти идентичные) в отношении рассматриваемых свойств.
Если «на входе» задачи классификации имеется лишь матрица «объект – свойство», каждая строка которой отражает значения измеренных у данного объекта свойств, и не имеется оснований для параметрического представления искомых классов, то такая классификация проводится методами кластерного анализа, а полученные классы объектов называют кластерами. Подобная ситуация часто встречается в социальных науках, поэтому для классификации объектов социологических, психологических, биологических и других исследований наиболее актуальными являются методы кластерного анализа.
В пакете SPSS реализованы 3 метода кластерного анализа: двухэтапный, метод k-средних и иерархический. Наиболее универсальным из них, применяемым к большим массивам данных и простым в интерпретации является метод k-средних. Рассмотрим особенности применения данного метода.
Выбрать тот или иной метод кластерного анализа пакета программ SPSS можно с помощью команд: Анализ → Классификация. Далее, в подменю команды Классификация необходимо:
1.Выбрать команду Кластеризация k-средними, которая реализует метод k-средних для заданного числа кластеров k.
2.Перенести все переменные, характеризующие свойства Х(1), Х(2), …, Х(р) матрицы «объект – свойство» Х в окно Переменные.
3.Указать в поле Метить наблюдения имя переменной, содержащей номера объектов классификации.
28
4.Задать в поле Число кластеров количество кластеров, на которое необходимо разбить исходное множество объектов. По умолчанию задается 2 кластера, сделать самостоятельную оценку числа кластеров можно с помощью разведочного анализа.
5.Кнопка Итерации позволяет увеличить максимальное число шагов алгоритма. Установленное по умолчанию количество итераций, равное 10, зачастую оказывается недостаточным.
6.Кнопка Сохранить позволяет указать для каждого объекта принадлежность в кластеру и расстояние до центра кластера, если установлен соответствующий указатель (галочка).
7.Кнопка Параметры позволяет вычислить дополнительные статистические величины, такие как начальные центры кластеров и другие, а также предоставляет возможность учесть пропущенные значения.
8.Запустить метод k-средних, нажав кнопку Ок.
Практическая часть
Задание 1
Дана выборка, состоящая из 8 объектов, каждый объект характеризуется по двум признакам. С помощью методов кластерного анализа разбить эту выборочную совокупность на 3 кластера следующими способами:
а) вручную, с помощью алгоритма k эталонов (использовать Евклидово расстояние), причем найти оптимальное разбиения для данных эталонов, минимизируя функционал качества Q1(S);
б) с помощью пакета SPSS, используя алгоритм k-средних;
в) проверить оптимальность выбора эталонов для первого метода с помощью результатов, полученных методом k-средних, в случае изменений пересчитать значение Q1(S) и сделать вывод.
Значения признаков х(1) и х(2) для эталонных точек и точек выборочной совокупности приведены в табл. 1 (Приложение 3).
29
Лабораторная работа 5
Реализация метода главных компонент с помощью пакета SPSS
Теоретическая часть
Факторный анализ является одним из наиболее мощных статистических средств анализа данных. В его основе лежит процедура объединения групп коррелирующих друг с другом переменных («корреляционных узлов») в несколько факторов.
Цель факторного анализа – сконцентрировать исходную информацию, выражая большое число рассматриваемых признаков через меньшее число более емких внутренних характеристик, которые, однако, не поддаются непосредственному измерению (являются латентными).
Метод главных компонент (МГК) является наиболее удобным и распространенным методом сокращения количества исходных наблюдаемых переменных и построения на их основе внутренних латентных переменных (главных компонент), описывающих большую часть суммарной дисперсии.
Напомним, что для применения МГК исходные данные должны быть представлены в виде матрицы Х «объект – свойство» размера n p, где n – это количество объектов для анализа, а р – количество
исходных наблюдаемых переменных.
В основу МГК положена линейная модель вида:
Yj p |
ajr Fr , |
j 1,2,..., p; |
r 1 |
|
|
где Y1,Y2 , ...,Yp – это стандартизированные значения р исходных
признаков, |
полученные из матрицы Х «объект – свойство»; |
F1, F2 , ..., Fp |
– это значения всех р главных компонент; ajr – это фак- |
торные нагрузки или веса r-й компоненты в j-й переменной, совпадающие с коэффициентами корреляции между главными компонентами и исходными переменными.
30
