
Гордобаева, Парыгина и др. Математика. Школа
.pdf
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«ЧЕРЕПОВЕЦКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Факультет общих математических и естественнонаучных дисциплин
Кафедра математики
МАТЕМАТИКА
ПОВТОРЕНИЕ ШКОЛЬНОГО КУРСА
Учебно-методическое пособие
Череповец
2013
Рассмотрено на заседании кафедры математики, протокол № 4 от 21.11.12 г. Одобрено редакционно-издательской комиссией Факультета общих математи-
ческих и естественнонаучных дисциплин ЧГУ, протокол № 3 от 27.11.12 г.
Составители: Т.В. Гордобаева, канд. техн. наук, доцент; С.А. Парыгина, канд. психол. наук, доцент; Н.В. Плотникова, канд. физ.-мат. наук, доцент; И.А. Сенатова, старший преподаватель
Рецензенты: Н.Н. Беляева, канд. пед. наук, доцент (ЧГУ); Е.А. Смирнова, канд. пед. наук, доцент (ЧГУ)
Научный редактор: А.В. Толстиков, канд. физ.-мат. наук, проф.
© Коллектив авторов, 2013 © ФГБОУ ВПО «Череповецкий госу-
дарственный университет», 2013
2
Введение
Настоящее учебно-методическое пособие подготовлено для студентов первого курса различных направлений подготовки бакалавриата и специалитета.
Пособие предназначено для организации практических занятий и самостоятельной работы студентов по повторению школьного курса математики и охватывает следующие разделы: «Тождественные преобразования алгебраических выражений», «Степени и корни», «Логарифмы», «Тригонометрия». Пособие содержит краткие теоретические сведения в виде опорного конспекта по каждому из вышеперечисленных разделов; примеры, иллюстрирующие как теоретические сведения, так и способы решения задач; а также двухуровневые задания для выполнения на практическом занятии и в процессе самостоятельной работы студентов. Задания 2-х уровней сложности позволяют осуществить дифференцированный подход в процессе повторения школьной программы, учитывая разный начальный уровень подготовки студентов.
Наличие в учебно-методическом пособии опорных конспектов по каждому из выбранных разделов школьной программы по математике позволяет не только повторить, но и систематизировать знания студентов, тем самым подготовив их к освоению дисциплины «Математика» в вузе.
3

Тема 1
ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ АЛГЕБРАИЧЕСКИХ ВЫРАЖЕНИЙ
1. Разложение многочленов на множители. Простейшим пре-
образованием алгебраических выражений является разложение их на множители. Для этого удобно использовать следующие формулы.
Формулы сокращённого умножения
1.Квадрат суммы: (a + b)2 = a2 + 2 × a ×b + b2
2.Квадрат разности: (a - b)2 = a2 - 2 × a ×b + b2
3.Разность квадратов: a2 - b2 = (a + b) × (a - b)
4.Куб суммы: (a + b)3 = a3 + 3 × a2 ×b + 3 × a ×b2 + b3
5.Куб разности: (a - b)3 = a3 - 3 × a2 ×b + 3 × a ×b2 - b3
6.Сумма кубов: a3 + b3 = (a + b) × (a2 - a ×b + b2 )
7.Разность кубов: a3 - b3 = (a - b) × (a2 + a ×b + b2 )
Разложение квадратного трехчлена на множители
|
a × x2 + b × x + c = a × (x - x ) × (x - x ), |
|||||
|
|
1 |
|
|
2 |
|
|
где x1, 2 = |
-b ± b2 - 4ac |
|
|
||
|
2a |
|
||||
|
|
|
||||
Пример 1. Разложите на множители: |
|
|||||
а) P ( x) = x4 |
- 2x3 + 2x2 - 2x +1 = x4 + 2x2 +1 - 2x3 |
- 2x = ( x2 +1)2 - 2x ´ |
||||
4 |
|
|
|
|
|
|
´(x2 +1) = ( x2 +1) ×(x2 - 2x +1) = (x2 +1) ×( x -1)2 ;
б) P2 ( x) = 3 - 2x2 - 5x = (-2) ×( x + 3) ×( x - 0,5) = (1 - 2x) ×( x + 3), так как
4
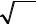
|
3 - 2x2 - 5x = 0 -2x2 - 5x + 3 = 0, |
|
|
|
||||||
|
D = (-5)2 - 4 × (-2) ×3 = 25 + 24 = 49, |
|
|
|
||||||
x = |
-(-5) + |
|
|
x = |
5 + 7 |
= -3, x = |
5 - 7 |
|
|
|
49 |
= |
1 |
. |
|||||||
|
|
|
|
|
|
|||||
1,2 |
2 × (-2) |
1 |
-4 |
2 |
-4 |
2 |
|
|||
|
|
|
|
|
||||||
Задание 1. Разложите на множители.
Вид заданий |
№ |
1 уровень |
|
|
2 уровень |
|
п/п |
|
|
||||
|
|
|
|
|||
|
1 |
x2 - y2 - x - y |
ax2 - bx2 + bx - ax + a - b |
|||
|
|
|
|
|||
|
2 |
c2 - x2 + 2xy - y2 |
x3 - 3x2 + 4x - 2 |
|||
Задания для |
3 |
7x3 + 7 y3 |
(ay + bx)2 + (ax - by)2 - c2 ×(x2 + y2 ) |
|||
4 |
ax2 - a - x2 + x |
(x - a)4 - ( x + a)4 |
||||
работы у дос- |
|
|
|
|
|
|
5 |
a4 + ax3 - a3 x - x4 |
x6 - ( yz)6 |
||||
ки |
||||||
6 |
2x2 + x - 6 |
x2 - 7x +12 |
||||
|
||||||
|
7 |
3 - x2 - 2x |
n2 + 2n - 8 |
|||
|
(сначала выделить полный квад- |
|||||
|
|
|
рат) |
|||
Задания для |
8 |
a2 - b2 + a3 - b3 |
81a8 -16c12 + 3a2 + 2c3 |
|||
самостоя- |
|
|
|
|
|
|
тельной рабо- |
9 |
2 - 3x - 2x2 |
x |
4 |
+1 (сначала выделить полный |
|
ты |
|
|
квадрат) |
|||
Задания для |
10 |
u4 + u3 + u +1 |
a4 - b2 ×(2a - b)2 |
|||
домашней ра- |
|
|
|
|
|
|
11 |
2x2 - 5x - 3 |
9x - 4x2 - 2 |
||||
боты |
||||||
2. Алгебраические дроби. Дробь, числитель и знаменатель которой являются многочленами, называется алгебраической дробью.
Например, следующие дроби:
2 |
, |
2xy |
, |
x + y |
, |
2x2 |
- y + x |
|
|
|
|
|
|||
a |
|
|
(a + b)3 |
||||
|
3x y z 3x - y |
|
|||||
являются алгебраическими дробями.
5

Область допустимых решений (ОДЗ) алгебраической дроби А
В
есть множество всех числовых наборов, соответствующих буквенному набору многочленов А и В, для каждого из которых числовое значение многочлена В не равно нулю.
Например, ОДЗ алгебраической дроби |
a(c2 |
+ d 2 ) |
есть множе- |
|
c |
+ d |
|||
|
|
ство всех числовых наборов, соответствующих её буквенному набору (a, c, d ), таких, что c ¹ -d .
На ОДЗ алгебраической дроби А справедливы равенства.
В
1. |
A |
= |
P × A |
, |
A |
= |
A / P |
, |
|
|
|
|
|||||
|
B P × B |
B B / P |
||||||
т. е. дробь не изменится, если её числитель и знаменатель умножить (разделить) на один и тот же многочлен Р = P(x) , не обращающийся в ноль на ОДЗ этой дроби.
2.А = − А = - А = - − А.
В-В -В В
|
Пример 2. Сократите дробь: |
|
|
|
|
|
|
|||||||||||
|
а) |
|
|
x4 -1 |
|
|
= |
x2 +1 |
при х ¹ ±1, х ¹ -2 ; |
|
|
|||||||
(x2 |
-1) × (x + 2) |
|
|
|
|
|
||||||||||||
|
|
|
|
|
x + 2 |
|
|
|
|
|
|
|||||||
|
б) |
2х - х2 - 3х3 |
= |
-(2х - х2 - 3х3 ) |
= |
3х3 + х2 - 2х |
= |
х×(3х2 + х - 2) |
= |
|||||||||
|
|
|
|
-(2 - 3х) |
|
|
|
|||||||||||
|
|
|
|
2 - 3х |
|
|
|
|
|
|
3х - 2 |
3х - 2 |
||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
х×3 × (х - |
|
) × (х +1) |
= |
х× (3х - 2) × (х +1) |
= х× (х +1) , |
|
|||||||||||
3 |
при (3х - 2) ¹ 0. |
|||||||||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
3х - 2 |
|
|
|
|
|
3х - 2 |
|
|
|
|
|
|
|||
6
Задание 2. Сократите дробь.
Вид заданий |
№ |
|
1 уровень |
|
|
2 уровень |
|||||||||||||||
|
п/п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
х3 + 8 |
|
|
|
|
|
|
(c + d ) × (a + b) |
|
|||||||||
|
|
х2 |
− 2х + 4 |
|
ac − bd + ad − bc |
||||||||||||||||
|
|
|
|
||||||||||||||||||
|
2 |
|
( х - 2)3 |
|
|
|
|
|
|
|
m2 + m × (a + b) + ab |
|
|||||||||
|
(2 |
- х)2 |
|
|
|
|
|
|
m2 - (a - b) × m - ab |
||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
Задания для |
3 |
|
5 - 3х - 2х2 |
|
|
p3 - 8q3 |
|
||||||||||||||
|
|
х3 - х |
|
|
|
|
|
|
p2 + 2 pq + 4q2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
работы у |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х2 - х |
|
|
|
|
|
|
4xy ×(( x + z)2 - y2 ) |
|
||||||||||
доски |
4 |
|
|
|
|
|
|
|
|
||||||||||||
|
2х2 + х - 3 |
|
z2 - x2 - y2 + 2xy |
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
5 |
|
|
х2 -1 |
|
|
|
|
|
|
x4 - y4 |
|
|||||||||
|
|
2х2 + х -1 |
|
x2 + y2 - 2xy |
|||||||||||||||||
|
|
|
|
||||||||||||||||||
|
6 |
|
3х2 - 2х -1 |
|
( x2 + y ×( x + y)) ×( x2 - y2 ) |
||||||||||||||||
|
|
|
1 - х2 |
|
|
|
|
|
|
( x3 + 3xy ×( x + y) + y3 ) ×( x3 - y3 ) |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
Задания для |
7 |
|
10х − 20 |
|
|
(m2 + 4mn + 4n2 ) ×(m2 - 4mn + 4n2 ) |
|
||||||||||||||
самостоя- |
|
2х2 - 3х |
- 2 |
|
|
|
m2 - 4n2 |
||||||||||||||
|
|
|
|
|
|||||||||||||||||
тельной ра- |
8 |
|
|
х2 - 9 |
|
|
|
|
|
|
a4 + a3b - ab3 - b4 |
||||||||||
боты |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2х2 + 5х |
- 3 |
|
|
((a + b)3 - a3 - b3 ) ×(a3 - b3 - (a - b)3 ) |
|||||||||||||||||
|
|
|
|
||||||||||||||||||
Задания для |
9 |
|
|
3х2 - х |
|
|
(ab + (a - b)2 ) ×((a + b)2 - ab) |
|
|||||||||||||
|
3х2 + 2х |
-1 |
|
|
(a - b)3 + 3ab ×(a - b) |
||||||||||||||||
|
|
|
|
||||||||||||||||||
домашней |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12х −18 |
|
|
a6 - b6 |
|
|||||||||||||||
работы |
10 |
|
|
||||||||||||||||||
|
|
2х2 - х - 3 |
|
((a + b)2 - ab) ×((a - b)2 - ab) |
|||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Операции над алгебраическими дробями. Приведение дробей к общему знаменателю. Общим знаменателем нескольких алгебраических дробей называется многочлен, который делится на знаменатель каждой из этих дробей.
Например, для дробей |
х |
и |
3х − 1 |
общими знаменателя- |
|
х + 2 |
|
||||
|
|
х - 2 |
|
||
ми будут многочлены |
(х + 2) × (х - 2) = х2 - 4; |
2 × (х2 - 4); |
|||
х× (х2 - 4). |
|
|
|
|
|
Общий знаменатель, на который делится любой другой общий знаменатель без остатка, называется наименьшим общим знамена-
7

телем. В приведённом примере наименьшим общим знаменателем будет многочлен х2 − 4 .
Приведение двух алгебраических дробей к наименьшему общему знаменателю позволяет полученные дроби сложить (вычесть) по правилу 1.
В свою очередь, произведение и частное двух алгебраических дробей выполняются по правилам 2 и 3.
Правило 1. Сумма (разность) двух алгебраических дробей с
одинаковым знаменателем равна дроби, знаменатель которой равен знаменателю этих дробей, а числитель – сумме (разности) их числителей, т. е.
A + B = A + B и A - B = A - B .
C C C C C C
Правило 2. Произведение двух алгебраических дробей равно дроби, знаменатель которой равен произведению знаменателей этих дробей, а числитель – произведению их числителей, т. е.
A × C = A×C .
B D B × D
Правило 3. Частное отделения двух алгебраических дробей
равно дроби, числитель которой равен произведению числителя первой дроби на знаменатель второй дроби, а знаменатель – произведению знаменателя первой дроби на числитель второй, т. е.
A : C = A× D
B D B ×C
(на множестве числовых наборов, для которых
B ¹ 0,C ¹ 0, D ¹ 0 ).
8
|
Пример 3. Выполните действия: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
а) |
|
|
5 - x |
+ |
|
|
6 - x |
|
- |
4 - x |
= |
(5 - x) × (x + y) + (6 - x) - (4 - x) × (x - y) |
= |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
x - y x2 - y2 |
|
|
|
|
|
x + y |
|
|
|
|
|
|
|
|
|
|
|
(x - y) × (x + y) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
= |
5x + 5 y - x2 - xy + 6 - x - 4x + 4 y + x2 - xy |
= |
|
9 y - 2xy + 6 |
, при |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 - y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 - y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
x2 - y2 ¹ 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
б) |
|
x2 + yx |
|
|
× |
3x3 - 3y3 |
|
= |
|
|
x × (x + y) ×3 × (x3 - y3 ) |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
5x2 - 5 y2 |
|
|
|
x2 - xy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 × (x2 - y2 ) × x × (x - y) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
= |
3 × (x + y) × (x - y) × (x2 + xy + y2 ) |
= |
3 × (x2 + xy + y2 ) |
, при |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
5 × (x - y) × (x + y) × (x - y) |
|
|
|
|
|
|
|
5 × (x - y) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
x × (x2 - y2 ) ¹ 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
в) |
|
m3 - n3 |
|
|
|
: |
mn + m2 |
|
|
|
= |
(m3 - n3 ) × (m2 - n2 ) |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
(mn - n2 )2 |
|
|
|
|
m2 - n2 |
|
|
|
|
|
|
(mn - n2 )2 × (mn + m2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
= |
(m - n) × (m2 + mn + n2 ) × (m - n) × (m + n) |
= |
m2 + mn + n2 |
|
, при |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
n2 × (m - n)2 × m × (n + m) |
|
|
|
|
|
|
|
|
|
|
|
|
n2 × m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
mn ¹ 0, m ¹ ±n . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Задание 3. Упростите выражение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Вид за- |
№ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 уровень |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 уровень |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
даний |
п/п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
|
|
|
1 - х2 |
|
|
|
|
|
|
|
|
a2 + b2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
−1 |
a2 - b2 |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
+ |
1 × |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
- a |
× |
|
|
|
- |
|
|
|
|
|
× |
|
a |
3 |
+ b |
3 |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
х +1 |
|
|
|
|
4х -1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b a |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Задания |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 - y +1 |
|
|
|
|
|
|
|
|
3y2 |
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||||||||||||||||||||||||
для ра- |
2 |
|
|
|
|
|
|
|
|
|
|
- y |
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
- |
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x4 - xy3 |
|
x3 + x2 y + y2 x |
x2 - xy |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
- y |
|
|
|
y |
2 |
- 2 y +1 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
боты у |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
доски |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
6a +1 |
|
|
|
|
|
|
6a -1 |
|
a2 |
- 36 |
|
|
|
|
|
1 |
|
|
|
|
+ |
|
|
|
|
2a |
|
|
|
|
+ |
|
|
|
|
|
1 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
+ 3a + |
|
|
|
2 |
+ 4a |
+ |
|
|
|
|
2 |
+ 5a + 6 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
× |
|
|
|
|
|
|
|
a |
|
|
2 a |
|
3 a |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
- |
|
|
|
|
|
|
|
|
2 |
+ |
|
|
|
|
|
a |
2 |
+1 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
a |
|
|
6a a |
|
6a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9
Продолжение
1 |
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
||
Задания |
|
|
|
2 |
|
+1 - |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
для са- |
|
|
|
х |
|
|
|
|
|
|
|
|
|
|
|
x |
3 |
- y |
3 |
|
|
|
2 y |
|
2 xy + 4 y |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 - 2х |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
мостоя- |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
× |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- 2 y - 2 x - xy |
|
|
|
|
2 - |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 y |
|
|
|
4 |
( x - y) × ( x |
4) |
||||||||||||||
|
|
|
х - |
4х |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
тельной |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
работы |
|
|
|
|
|
|
|
|
2х -1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Задания |
|
|
|
|
|
a |
2 |
+ b |
2 |
|
|
|
1 |
|
2 |
|
х + 7 |
|
|
|
|
х + 7 |
|
|
|
х + 5 |
х + 3 |
−2 |
||||||||||||||
для до- |
|
|
|
|
|
|
|
|
|
|
|
|
× |
|
|
|
|
+ |
|
|
|
|
× |
|
|
|
|
|||||||||||||||
машней |
5 |
a |
- |
|
|
|
|
|
|
|
|
× |
|
|
|
+ |
|
|
|
х + 9 |
|
|
х2 + 81 - |
18х х2 - 81 х |
- 9 |
|
|
|||||||||||||||
|
a + b |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
b |
|
a - b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
работы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Нахождение значения алгебраического выражения. Для того, чтобы найти значение алгебраического выражения, удобно его сначала упростить с помощью приёмов и методов, изученных в предыдущих пунктах.
Пример 4. Упростите выражение и вычислите:
|
|
|
|
|
|
(a - b) |
2 |
|
|
|
|
+ b) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1+ |
|
|
× |
(a |
|
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|||||||||||||||||
|
|
|
ab |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
4 |
|
3 |
|
|
|
3 |
- b |
4 |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
ab |
|
|
|
|
|
|
|
× |
|
|
|
|
|
|
|
|
|
|
+ a b - ab |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
a |
4 |
3 |
|
|
|
|
3 |
- b |
4 |
|
|
|
|
|
|
|
3 |
- a |
3 |
3 |
) ×(a |
3 |
- b |
3 |
3 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
- a b + ab |
|
|
|
|
|
|
|
((a + b) |
|
|
- b |
|
|
|
- (a - b) |
) |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
2 |
- 2ab + b |
2 |
|
|
|
|
2 |
|
+ 2ab + b |
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 + |
|
|
|
|
× |
(a |
|
|
|
-1 |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ab |
|
|
|
|
|
|
|
|
|
|
|
|
|
ab |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
´ |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a4 - a3b + ab3 - b4 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
´ |
|
|
(a3 |
+ 3a2b + 3ab2 + b3 - a3 - b3 ) × (a3 - b3 - (a3 - 3a2b + 3ab2 - b3 )) |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
4 |
|
|
|
3 |
|
|
|
|
|
3 |
- b |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ a b - ab |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
ab + a2 - 2ab + b2 |
|
× |
|
a2 + 2ab + b2 - ab |
|
|
|
(3a2b + 3ab2 ) × (3a2b - 3ab2 ) |
|
|||||||||||||||||||||||||||||||||||||||
= |
|
|
|
|
|
|
|
ab |
|
|
|
|
|
|
|
|
|
|
|
|
|
ab |
|
|
|
|
|
|
|
× |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
a4 - a3b + ab3 - b4 |
|
|
|
|
|
|
|
|
|
|
|
|
a4 + a3b - ab3 - b |
|
|
|
|
|||||||||||||||||||||||||
=
=
=
10
