3. Спектр атома водорода

Вид оптических спектров атомов определяется их энергетические спектром. Методами квантовой механики можно получить точное и полное описание спектра для атома, имеющего один электрон, т.е. для атома водорода (и водородоподобных ионов), в то время как задача о многоэлектронных атомах может быть решена лишь приближенно. Можно показать, каким образом в квантовой механике возникает квантование энергии.

Атом является квантовой системой и для его описания следует применить квантово-механическое уравнение Шредингера. Запишем уравнение Шредингера для стационарных состояний:

, (2)

где − лапласиан (оператор Лапласа) (в декартовых координатах лапласиан равен:),

− масса рассматриваемой частицы,

− полная энергия частицы,

− потенциальная энергия частицы во внешнем поле,

− волновая функция частицы.

Решая уравнение (2), находят волновые функции частицы. Для атома водорода, например, -функция для основного состояния имеет вид , где− боровский радиус (м).

Волновая функция должна удовлетворять так называемым стандартным условиям, т.е. должна быть конечной, однозначной и непрерывной (её производная, кроме того, также должна быть однозначной и непрерывной). Эти условия могут выполниться лишь при определенных значениях полной энергии электрона . Это и означает, что энергия атома может принимать лишь определенные, дискретные значения, т.е. энергия квантуется.

В задаче об атоме водорода волновая функция удовлетворяет стандартным условиям лишь при значениях энергии

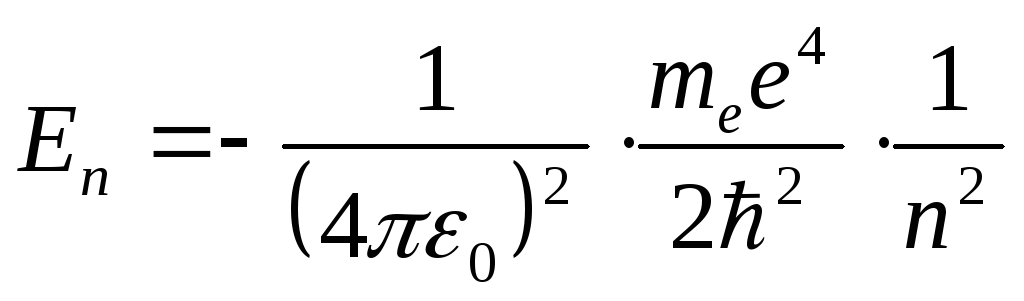, (3)

где Ф/м − электрическая постоянная,

− масса электрона (кг).

Знак минус означает, что электрон находится в связанном состоянии. Число , определяющее значение энергии, называется главным квантовым числом. Такие же значения энергии атома водорода получаются и в “полуклассической” (или “полуквантовой”) теории Бора.

Схема уровней энергии, определяемых формулой (3), дана на рис. 2. Совокупность спектральных линий для атома водорода, таким образом, определяется выражением

, (4)

где − постоянная Ридберга,с^-1,

и− главные квантовые числа (,).

Формула (4) называется формулой Бальмера-Ритца.

Линии в спектре атома водорода группируется вспектральные серии. При и получаетсясерия Лаймана (переходы с верхних уровней на основной). Эта серия находите я в УФ области спектра и не видна глазом. При и получаетсясерия Бальмера. Она находится в видимой части спектра, и именно она наблюдается и изучается в данной лабораторной работе. Следующая серия соответствует и . Она называетсясерией Пашена и лежит в невидимой ИК-области спектра. Имеются и другие серии: −серия Брэкета,−серия Пфунда,−серия Хамфри (рис. 2).

4. Расчет длин волн видимых линий спектра атома водорода

Учитывая, что глаз человека воспринимает свет с длинами волн 400 - 800 нм, и, пользуясь формулой Бальмера-Ритца, определите, сколько линий атома водорода попадает в видимую часть спектра.

II. Порядок выполнения работы

Целью лабораторной работы является изучение спектра испускания атомарного водорода, вычисление постоянной Ридберга и энергии ионизации атома водорода. Изучить спектр испускания − значит перечислить линии, наблюдаемые в спектре данного вещества и указать соответствующие им длины волн.