Практична робота_1

Практична робота №1

“Побудова графіків функцій та знаходження

коренів рівняння”

Зразок виконання завдань до практичної роботи №1.

Мета роботи. Дана робота має надзвичайно важливе значення для оволодінням студентом навичків роботи з електронною таблицею. Вводиться поняття Автозаповнення числового діапазону. Потім студент переходить до побудови формул і правильного використання функцій у формулах. Чи не найперше у цій роботі він стикається з поняттям логічної функції, вивчає синтаксис або структуру цієї функції і правила використання цієї функції. У цій роботі студент навчається використання засобу Мастер функций і за допомогою Мастера диаграм одержувати графік функції. Також у даній роботі студент знайомиться з поняттям абсолютного і напівабсолютного адреса.

(а) Побудувати в різних системах координат при хє[-1,8;1,8] графіки слідуючих функцій:

a1) y= , a2) g=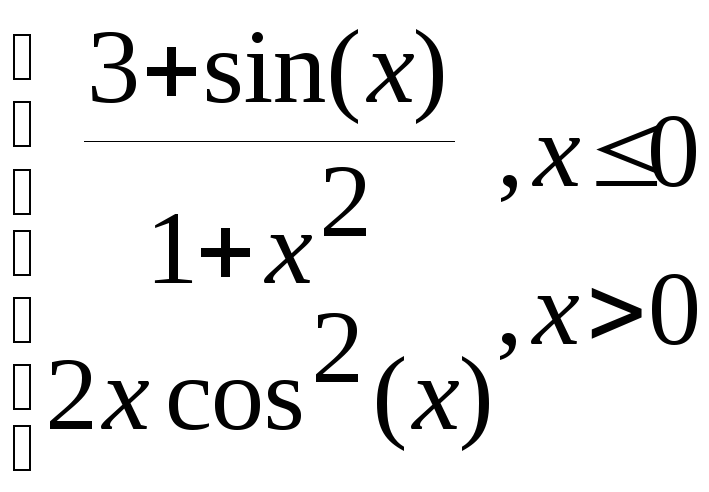

a3) z=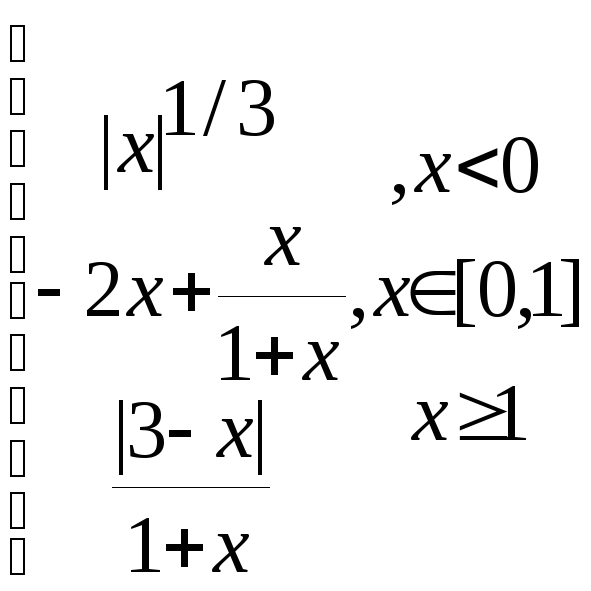

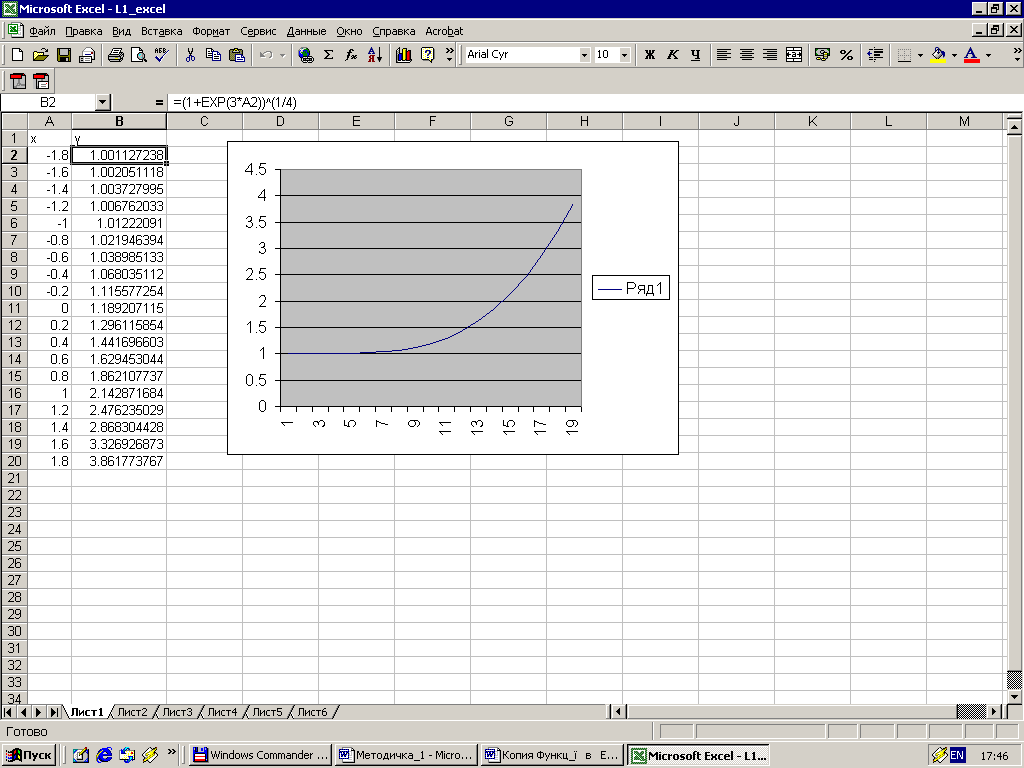
a1) Розглянемо діапазон [-1,8;1,8]. На чистому робочому аркуші у комірку А1 заносимо x, а в В1 у. Значення х повинні братися в діапазоні [-1,8; 1,8]. Якщо взяти за крок розрахунку 0,2, то в А2 заносимо –1,6. Далі нам потрібно використати такий механізм як Автозаповнення. Для цього виділяємо комірки А2 і А3. У правому нижньому куті знаходиться чорний квадратик. Наблизимо курсор миші до цього квадратика так, що настане момент і курсор перетвориться у тонкий чорний хрестик. В цей момент натискуємо ліву кнопку миші і робимо протяжку курсора вниз. Збоку курсора будуть з’являтися значення –1,4, -1,2, ... Останнє значення, яке нам потрібне, буде 1,8. Припинимо рух курсора і звільняємо ліву кнопку миші.

Потім виділяємо комірку В2. Курсор ставимо в рядок формул і починаємо набирати формулу:

=(1+EXP(3*A2))^(1/4)

Формулу набіраємо без проміжків. Після набору формули натискуємо клавішу Enter. Якщо формулу набрали правильно то в В2 одержимо значення –1,001127238. У цій формулі є ехпоненціальна функція. Її можна було вставити за допомогою Мастер функций. Для цього потрібно виконати команду ВСТАВКА – ФУНКЦИЯ. Подальші дії описані вище в теоретичній частині.

Далі копіюємо формулу з комірки В2 у діапазон комірок В3:В20. Одержимо ряд значень функції у.

Для побудови графіку функції виділимо діапазон комірок А2:В19. далі запускаємо Мастер функций і за його допомогою одержуємо графік функції.

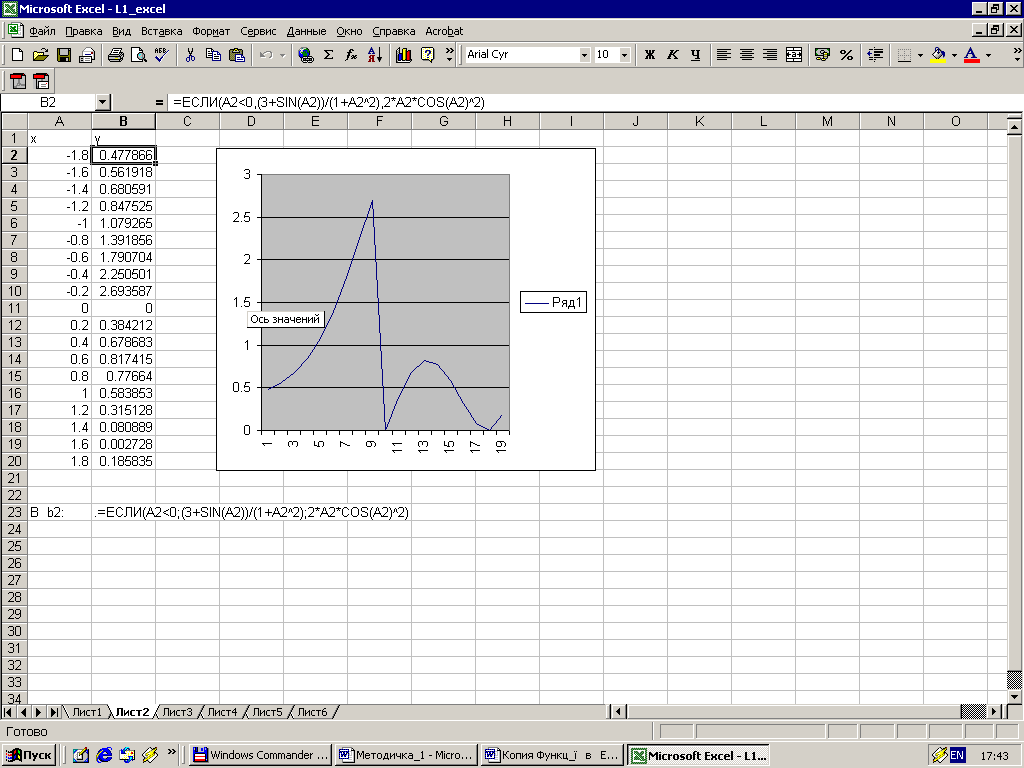
а2) Для даного прикладу повторюємо дії з попереднього прикладу. У комірку В2 заносимо слідуючу формулу:

=ЕСЛИ(A2<0,(3+SIN(A2))/(1+A2^2),2*A2*COS(A2)^2)

Функція ЕСЛИ() має три аргументи. Перший аргумент це логічна умова, другий і третій аргументи це обчислювальні вирази. Якщо логічна умова видає значення ІСТИНА, то обчислюється перший вираз, якщо ж логічна умова видає протилежне значення, то обчислюється другий вираз.

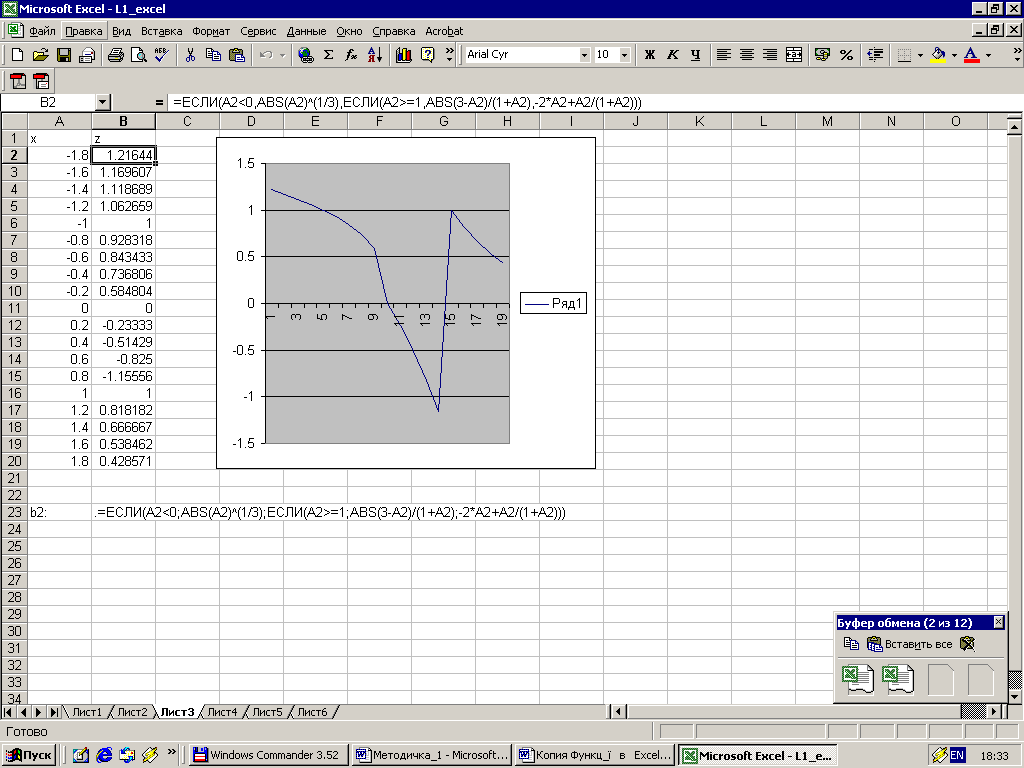
а3) Графік будуємо так само, як і в попередніх випадках, лише у комірку В2 заноситься слідуюча формула:

=ЕСЛИ(A2<0,ABS(A2)^(1/3),ЕСЛИ(A2>=1,ABS(3-A2)/(1+A2),-2*A2+A2/(1+A2)))

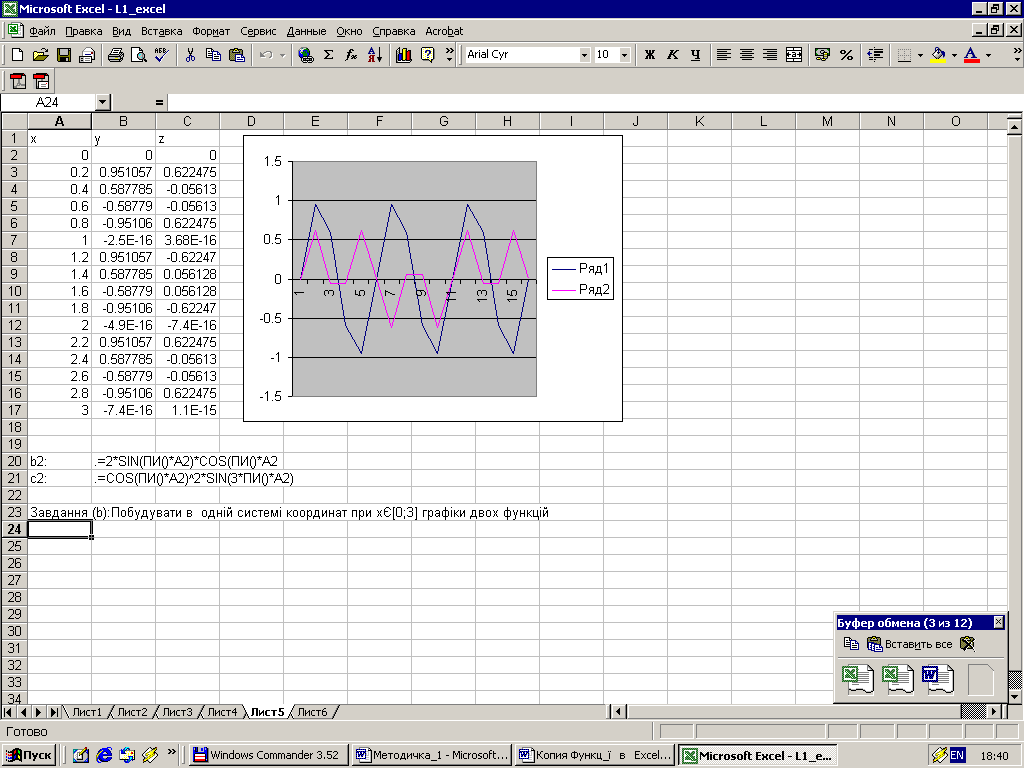
(b) Побудувати в одній системі координат при хє[0;3] графіки слідуючих двох функцій:

y=2sin(x)cos(x), z=cos²(x)sin(3x).

(c) Побудувати поверхню z=2x²cos²(x)-2y² при x,y[-1,1].

(d) Знайти всі корені рівняння

x³+0,54x²-2,7889x-1,506006=0.

У даній роботі рівняння такого типу створені штучно. Корені для рівнянь підбиралися в діпазоні (-3, 3). Нехай а, в, с є корені кубічного рівняння. Створимо такий алгебраїчний вираз (х-а)(х-в)(х-с)-0. Якщо розкрити дужки, то одержимо кубічне рівняння. До речі зауважимо, що такі перетворення зручно виконувати у пакеті Derive 6, у якому вони і виконувалися.

Отже спочатку ми виконуємо дії, аналогічні діям у пункті а1). Власне кажучи робити графік при виконанні цього завдання не обов’язково, але він надає нашим діям начності і упевненності.

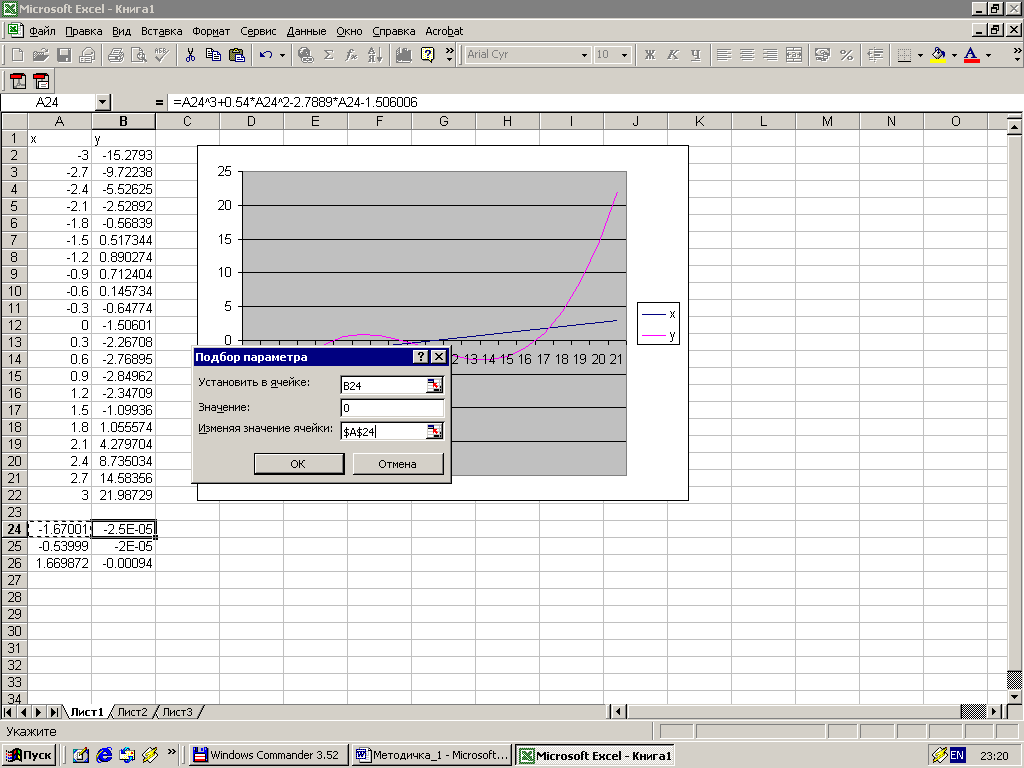
У комірки А24, А25, А26 заносимо такі значення –1,7, -0,5, 1,6 відповідно. У комірки В24, В25, В26 копіюємо формулу з комірки В22. Потім виділяємо комірку В24, виконуємо команду Сервис – Подбор параметра. Робимо установки, як на малюнку і натискуємо кнопку ОК. Одержимо у комірці В24 результат. Потім для завершення задачі повторюємо ці дії ще двічі.

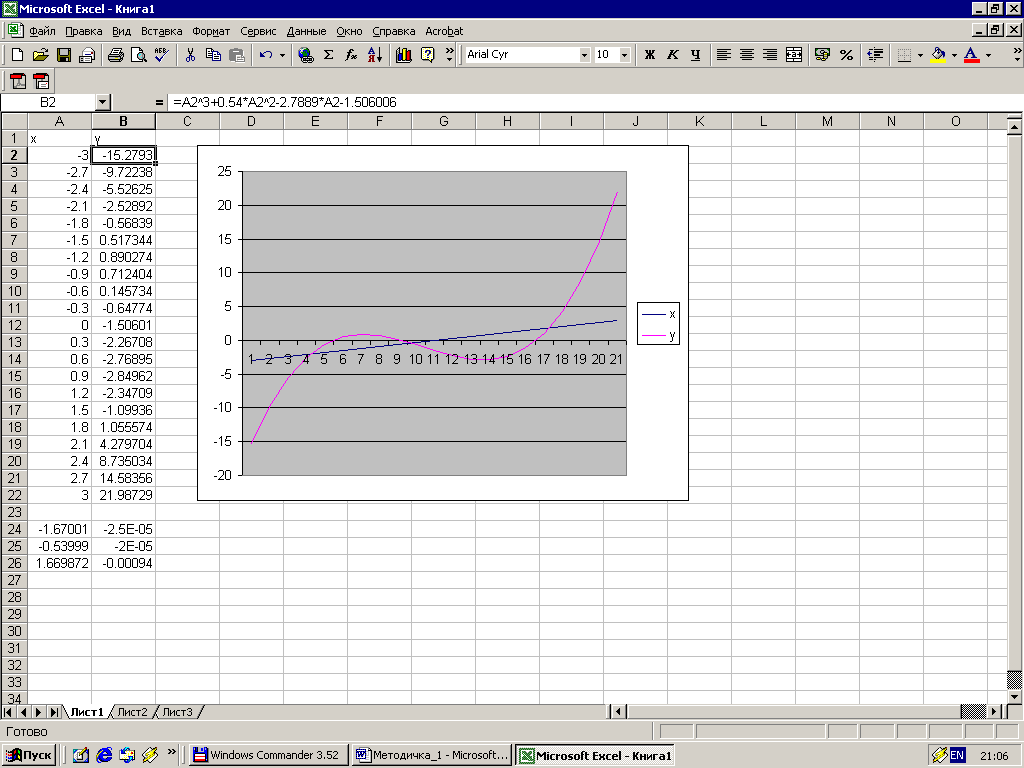
Так виглядає виконане завдання на робочому аркуші.

Завдання до виконання практичної роботи №1

Варіант 1

(а) Побудувати в різних системах координат при хє[-2;2] графіки слідуючих функцій:

y=sin(x)e^-2x , g=

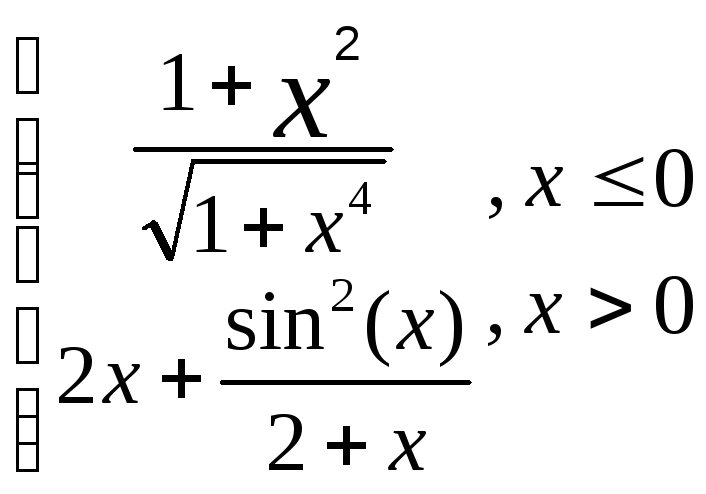
z=

(b) Побудувати в одній системі координат при хє[-2;2] графіки слідуючих двох функцій:

y=2sin(x)cos(x), z=3cos²(2x)sin(x).

(c) Побудувати поверхню z=x²-2y² при x,y[-1,1].

(d) Знайти всі корені рівняння

x³-1,86x²-3,0699x+2,422224=0.

Варіант 2

(а) Побудувати в різних системах координат при хє[-2;2] графіки слідуючих функцій:

y= , g=

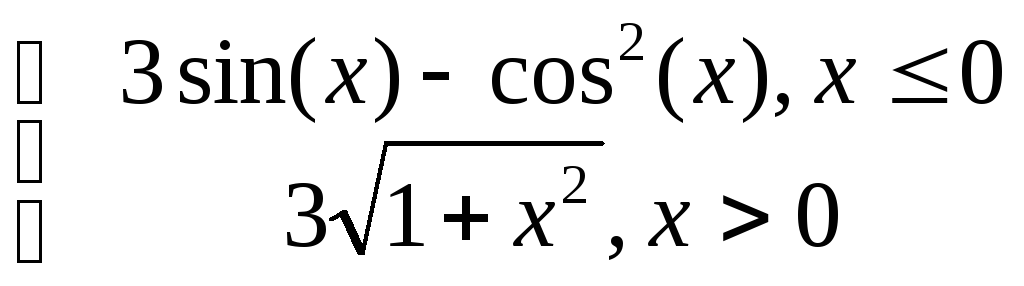
z=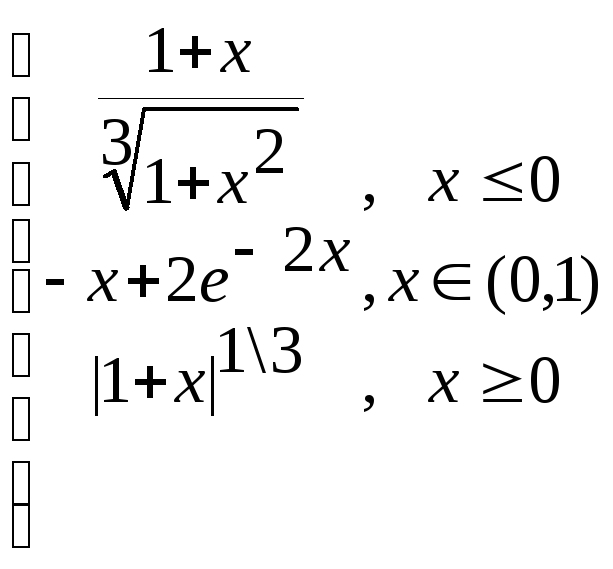

(b) Побудувати в одній системі координат при хє[-2;2] графіки слідуючих двох функцій:

y=2sin(x)-3cos(x), z=cos²(2x)-2sin(x).

(c) Побудувати поверхню z=3x²-2sin²(y)y² при x,y[-1,1].

(d) Знайти всі корені рівняння

x³+2,53x²-0,532x-2,849644=0.

Варіант 3

(а) Побудувати в різних системах координат при хє[-2,5;1,5] графіки слідуючих функцій:

y= , g=

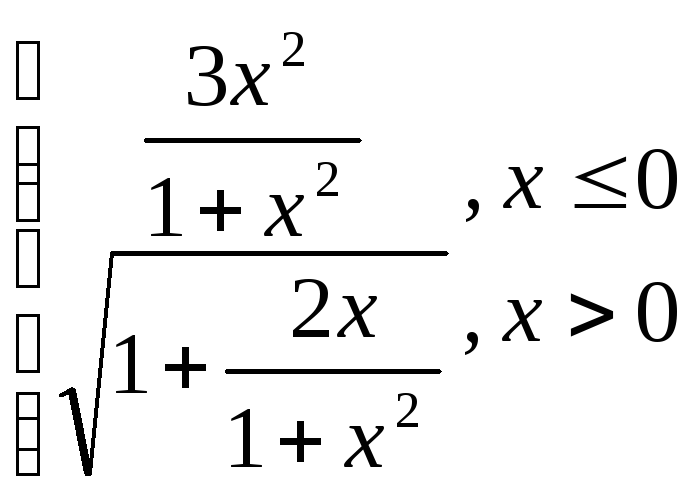
z=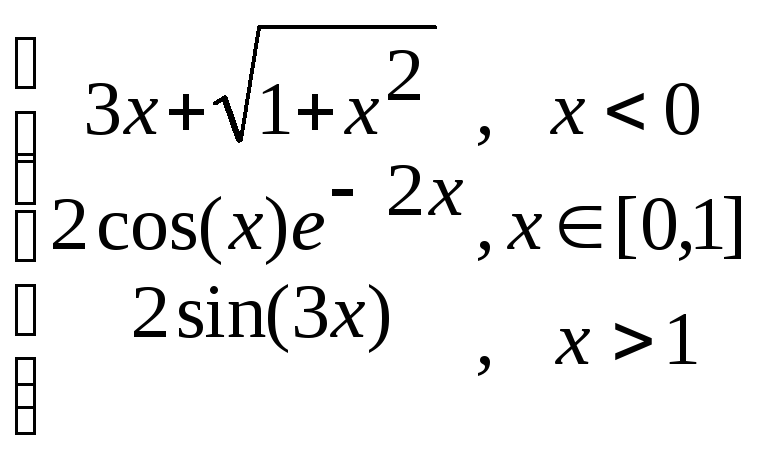

(b) Побудувати в одній системі координат при хє[-2;2] графіки слідуючих двох функцій:

y=5sin(x)-cos(3x)sin(x), z=cos(2x)-2sin³(x).

(c) Побудувати поверхню z=5x²cos²(y)-2y²e^y при x,y[-1,1].

(d) Знайти всі корені рівняння

x³+0,83x²-4,485x+0,774576=0.

Варіант 4

(а) Побудувати в різних системах координат при хє[-1,5;1,5] графіки слідуючих функцій:

y= , g=

z=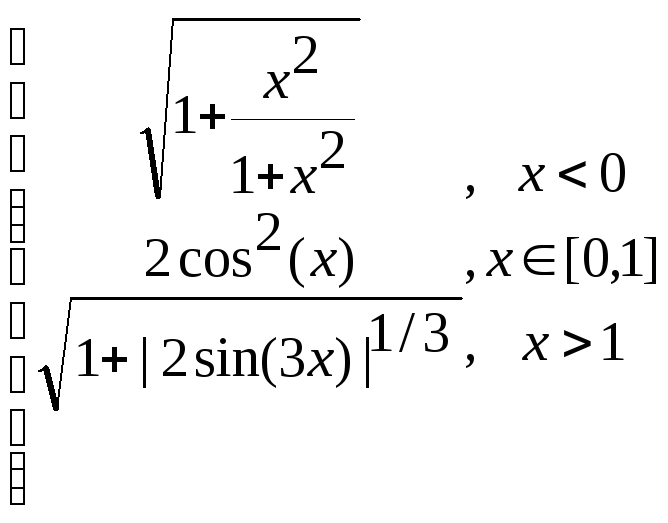

(b) Побудувати в одній системі координат при хє[-2;2] графіки слідуючих двох функцій:

y=3sin(2x)cos(x)—cos²(3x), z=2cos²(2x)-3sin(3x).

(c) Побудувати поверхню при x,y[-1,1]

z=

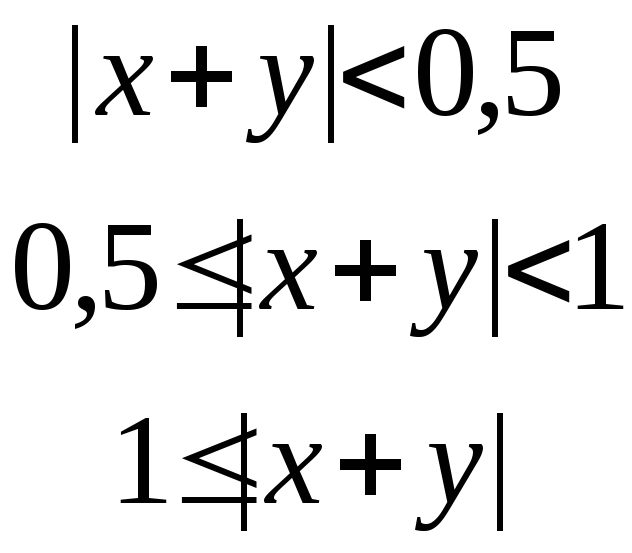
(d) Знайти всі корені рівняння

x³-0,56x²-6,1785x+1,814472=0.

Варіант 5

(а) Побудувати в різних системах координат при хє[-1,8;1,8] графіки слідуючих функцій:

y= , g=

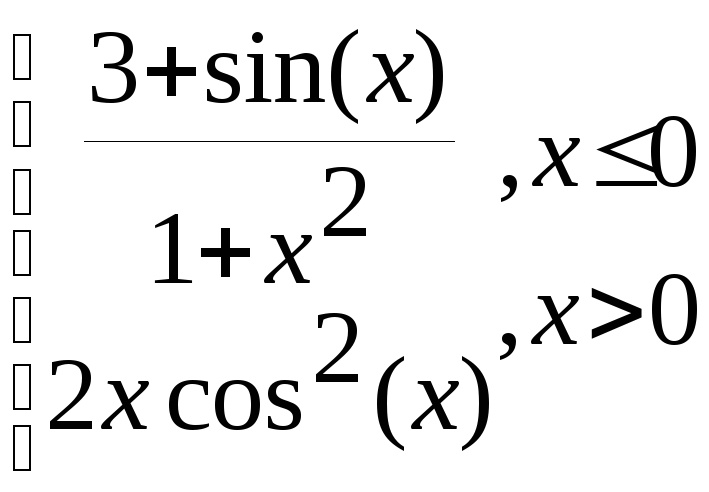
z=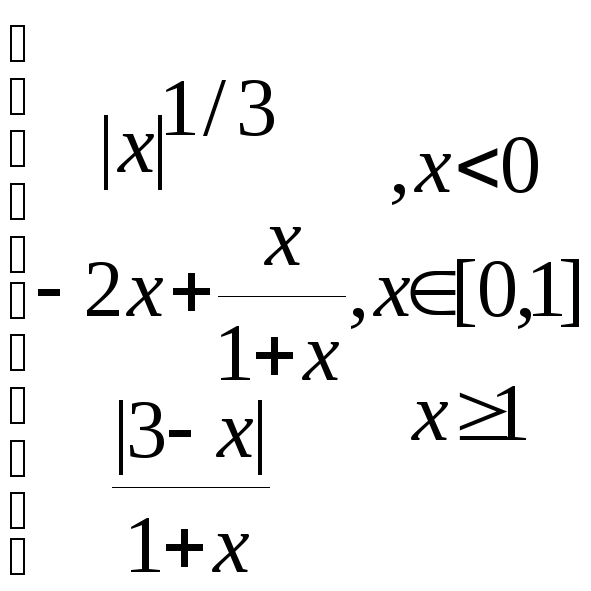

(b) Побудувати в одній системі координат при хє[0;3] графіки слідуючих двох функцій:

y=2sin(x)cos(x), z=cos²(x)sin(3x).

(c) Побудувати поверхню z=2x²cos²(x)-2y² при x,y[-1,1].

(d) Знайти всі корені рівняння

x³+0,54x²-2,7889x-1,506006=0.

Варіант 6

(а) Побудувати в різних системах координат при хє[-1,8;1,8] графіки слідуючих функцій:

y= g=

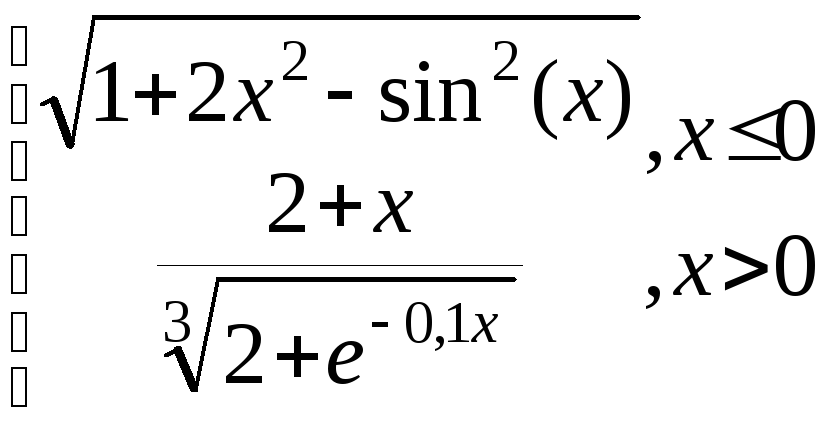
z=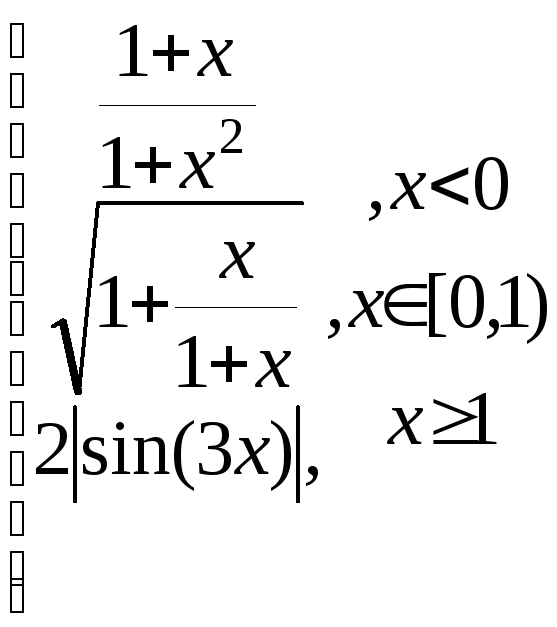

(b) Побудувати в одній системі координат при хє[0;3] графіки слідуючих двох функцій:

y=3sin(3x)cos(2x), z=cos³(4x)sin(x).

(c) Побудувати поверхню z=2e^0,2xx²-2y⁴ при x,y[-1,1].

(d) Знайти всі корені рівняння

x³+0,94x²-4,5369x-4,264686=0.

Варіант 7

(а) Побудувати в різних системах координат при хє[-1,7;1,5] графіки слідуючих функцій:

y= g=

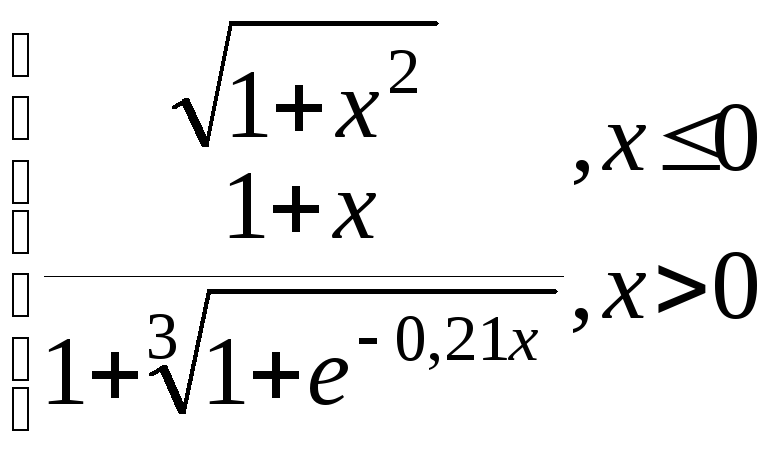
z=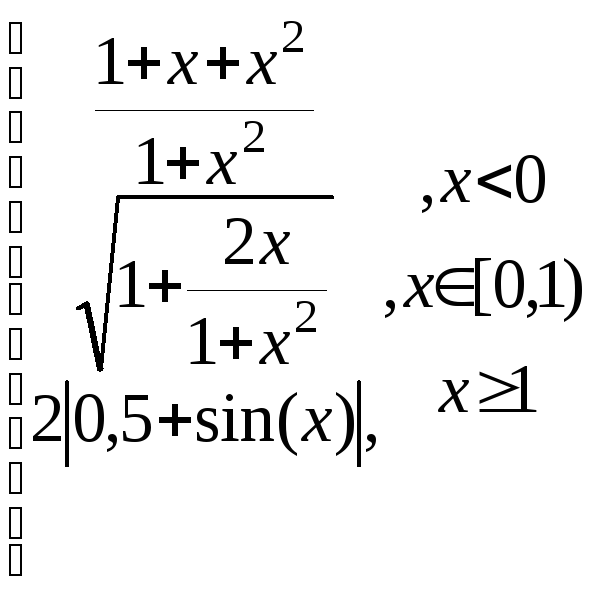

(b) Побудувати в одній системі координат при хє[-3;0] графіки слідуючих двох функцій:

y=2sin(2x)cos(4x), z=cos²(3x)-cos(x )sin(x).

(c) Побудувати поверхню z=x²-2e^0,2yy² при x,y[-1,1].

(d) Знайти всі корені рівняння

x³+0,6x²-2,8459x-0,28959=0.

Варіант 8

(а) Побудувати в різних системах координат при хє[-1,7;1,5] графіки слідуючих функцій:

y=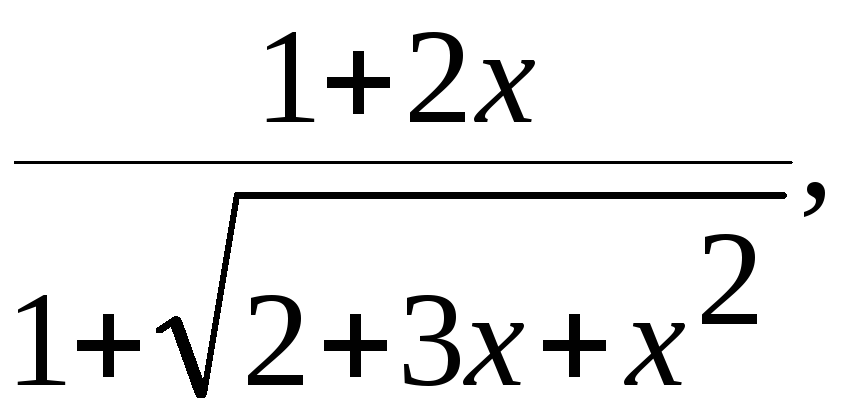 g=

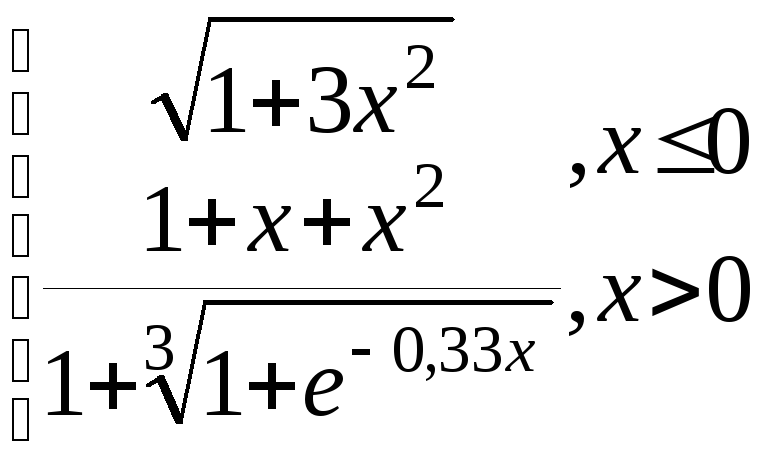
z=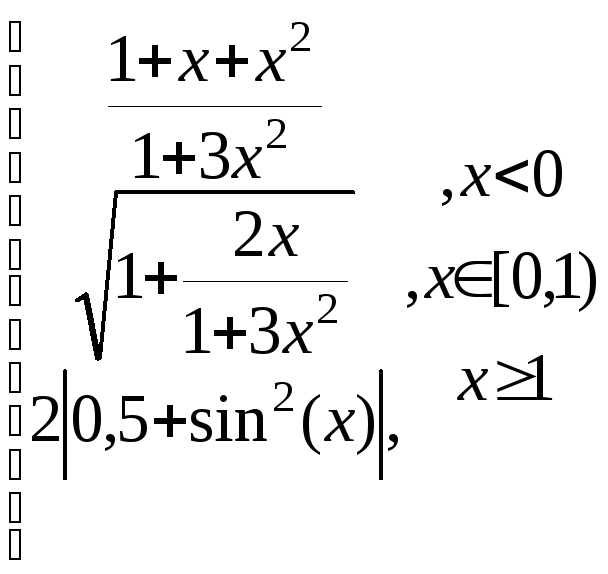

(b) Побудувати в одній системі координат при хє[-3;0] графіки слідуючих двох функцій:

y=2sin²(2x)cos³(4x), z=cos²(3x)-cos³(x )sin(x).

(c) Побудувати поверхню z=x²-2e^0,3yy² при x,y[-1,1].

(d) Знайти всі корені рівняння

x³+2,23x²-3,3161x-5,591703=0.

Варіант 9

(а) Побудувати в різних системах координат при хє[-1,7;1,5] графіки слідуючих функцій:

y=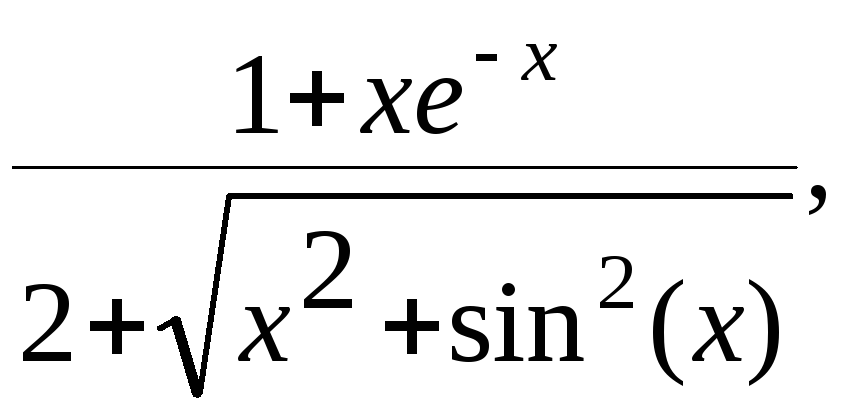 g=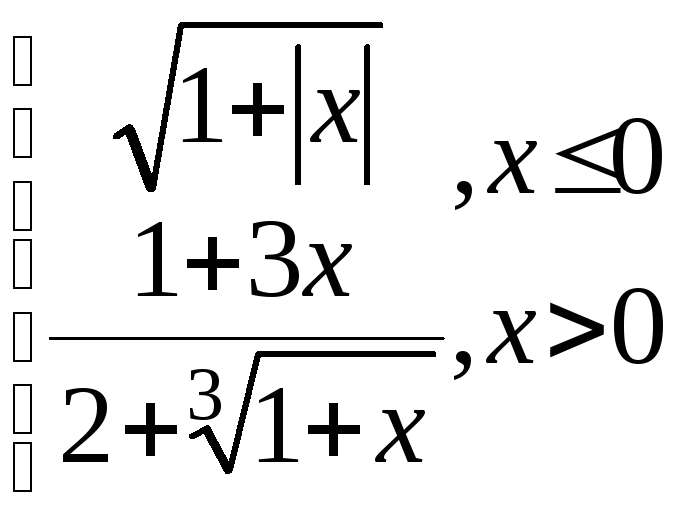

z=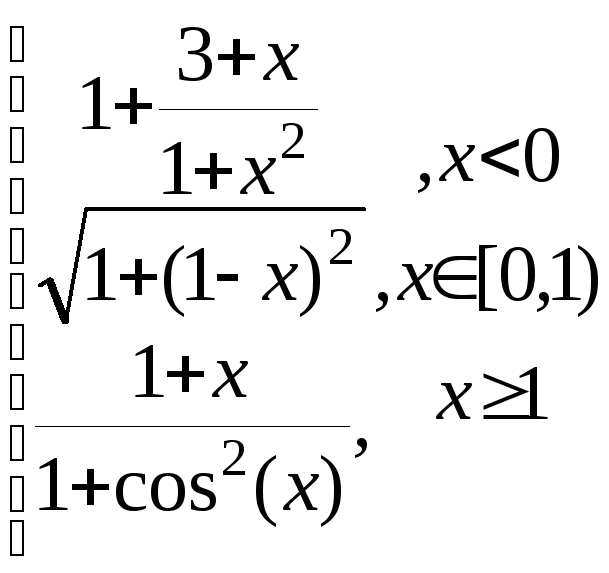

(b) Побудувати в одній системі координат при хє[0;2] графіки слідуючих двох функцій:

y=sin(3x)+2sin(2x)cos(3x), z = cos(x)-cos(3x )sin²(x).

(c) Побудувати поверхню z = x - e^2y при x,y[-1,1].

(d) Знайти всі корені рівняння

x³+2,27x²-0,3693x-1,421775=0.

Варіант 10

(а) Побудувати в різних системах координат при хє[-1,7;1,5] графіки слідуючих функцій:

y=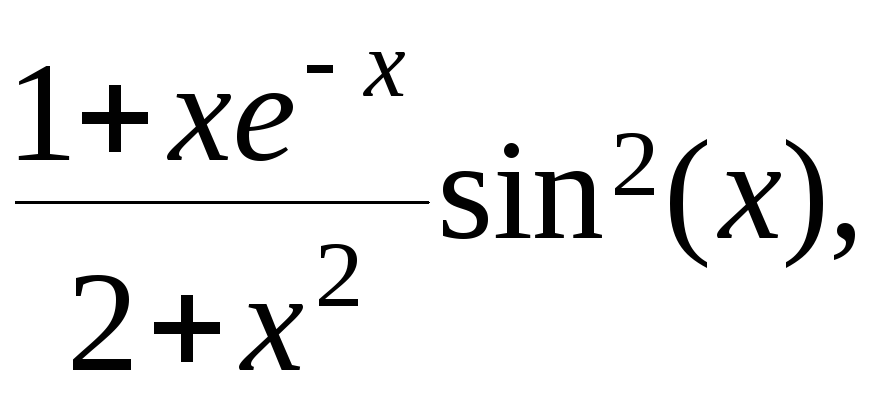 g=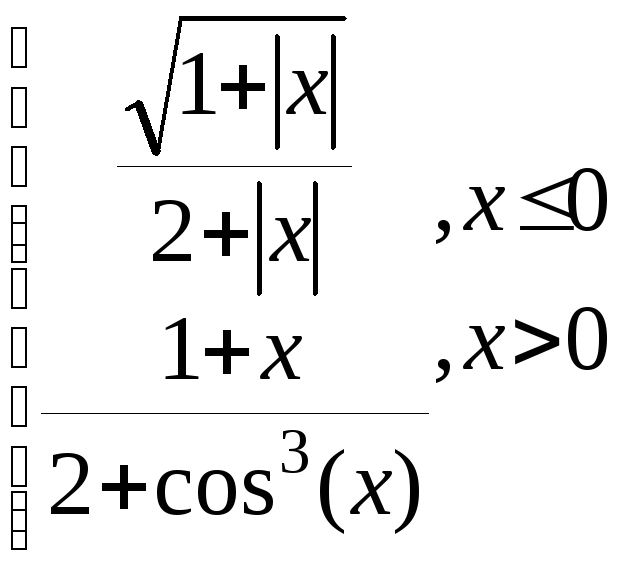

z=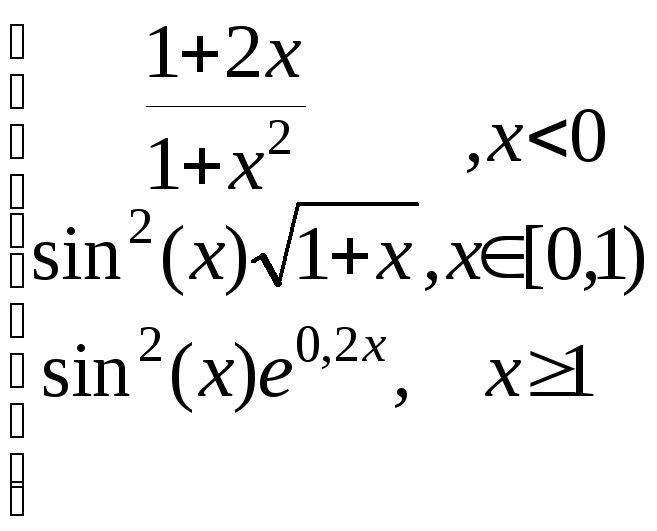

(b) Побудувати в одній системі координат при хє[0;2] графіки слідуючих двох функцій:

y=cos(3x)sin(x)+2sin(3x)cos(2x) , z=cos²(x)-cos(3x).

(c) Побудувати поверхню z=

(d) Знайти всі корені рівняння

x³+x²-1,4253x-0,438048=0.

Варіант 11

(а) Побудувати в різних системах координат при хє[-1,7;1,5] графіки слідуючих функцій:

y=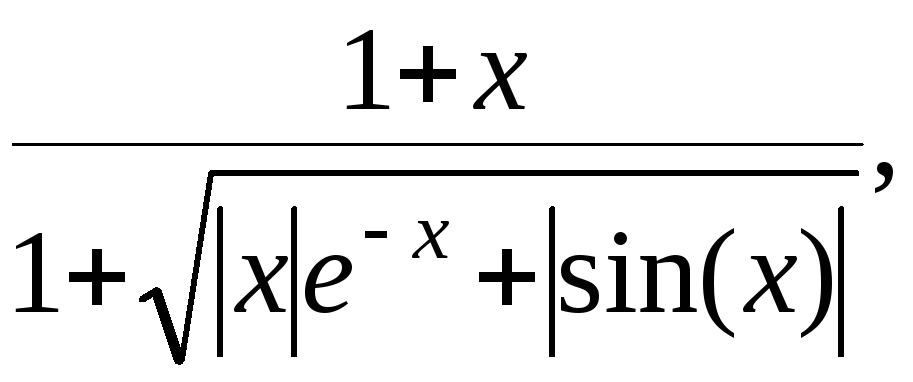 g=

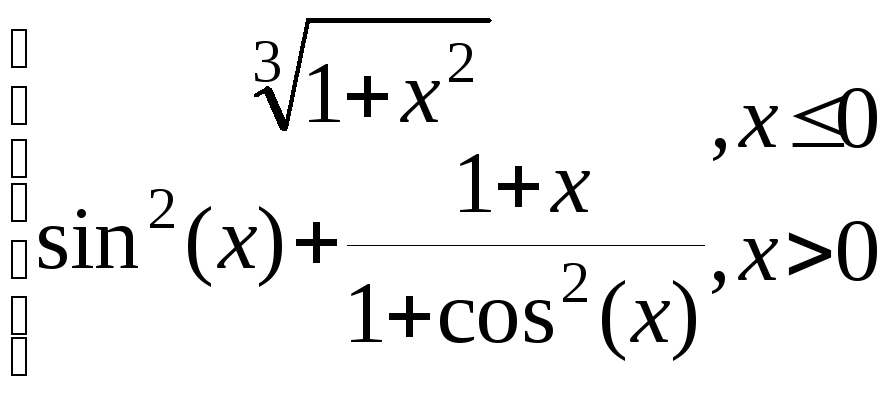
z=

(b) Побудувати в одній системі координат при хє[0;2] графіки слідуючих двох функцій:

y=2sin(2x)cos(x)+sin(3x), z=cos(2x)sin²(x)-cos(4x).

(c) Побудувати поверхню z=3x²sin²(x)-5e^2yy при x,y[-1,1].

(d) Знайти всі корені рівняння

x³+0,38x²-3,4255x+0,995596=0.

Варіант 12

(а) Побудувати в різних системах координат при хє[-1,7;1,5] графіки слідуючих функцій:

y=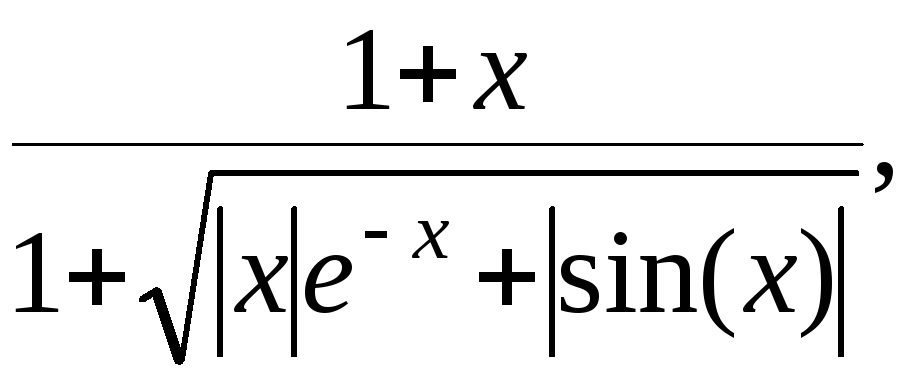 g=

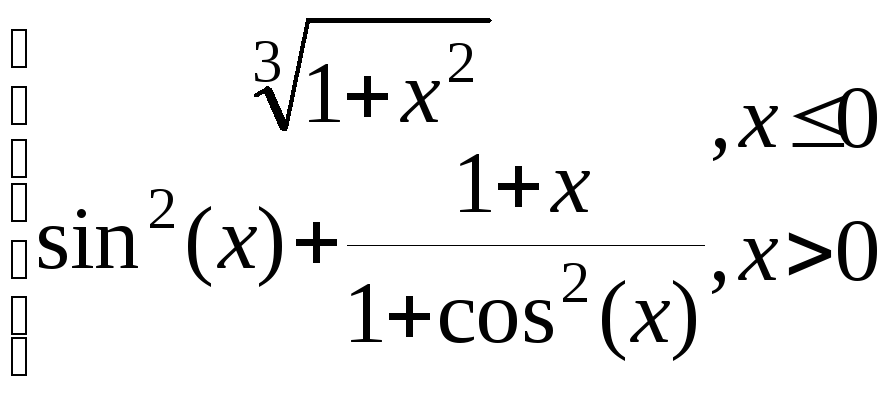
z=

(b) Побудувати в одній системі координат при хє[-2;2] графіки слідуючих двох функцій:

y=2sin(x)cos(x), z=3cos²(2x)sin(x).

(c) Побудувати поверхню z=x²-2y² при x,y[-1,1].

(d) Знайти всі корені рівняння

x³-0,33x²-4,2489x+0,555737=0.

Варіант 13

(а) Побудувати в різних системах координат при хє[-1,7;1,5] графіки слідуючих функцій:

y=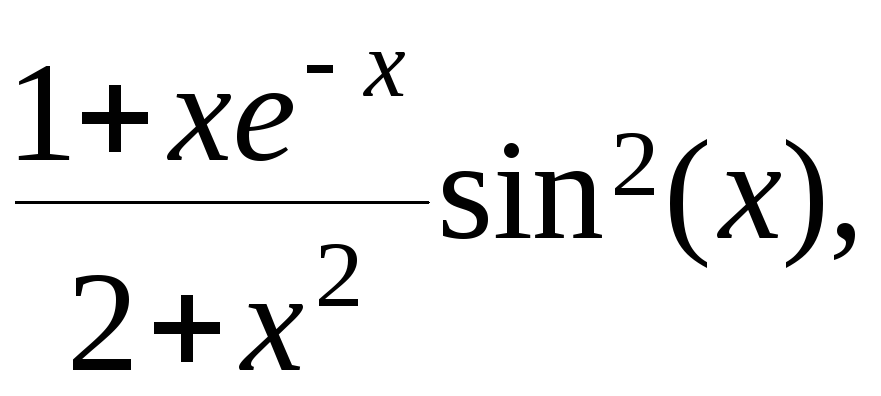 g=

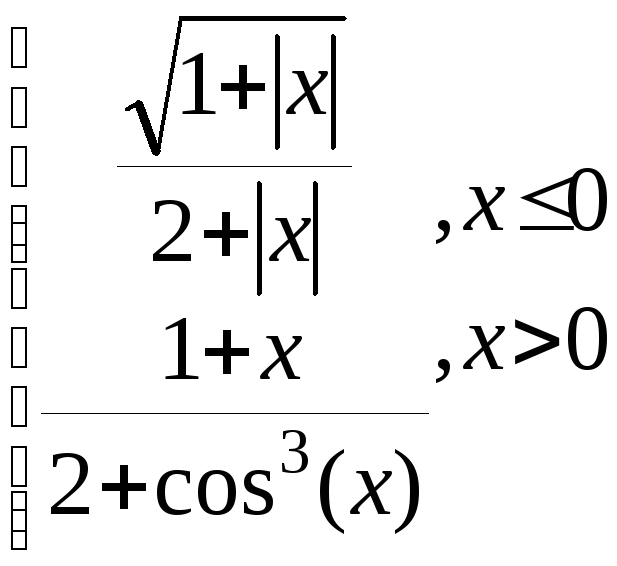
z=

(b) Побудувати в одній системі координат при хє[-2;2] графіки слідуючих двох функцій:

y=2sin(x)-3cos(x), z=cos²(2x)-2sin(x).

(c) Побудувати поверхню z=3x²-2sin²(y)y² при x,y[-1,1].

(d) Знайти всі корені рівняння

x³-0,29x²-5,1841x+2,396765=0.

Варіант 14

(а) Побудувати в різних системах координат при хє[-1,7;1,5] графіки слідуючих функцій:

y= g=

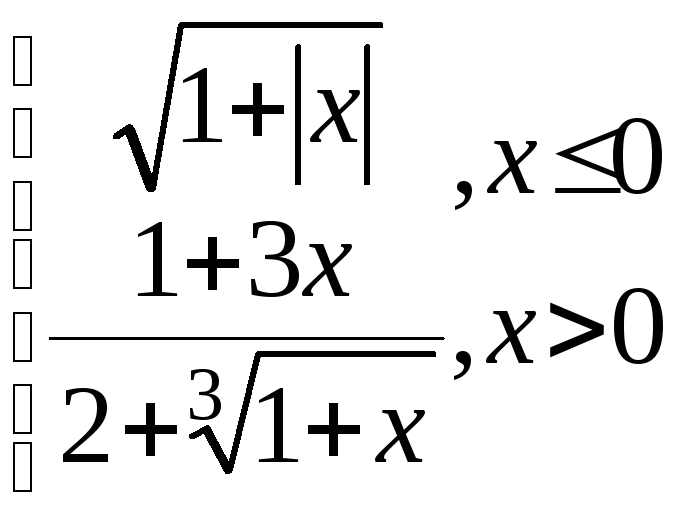
z=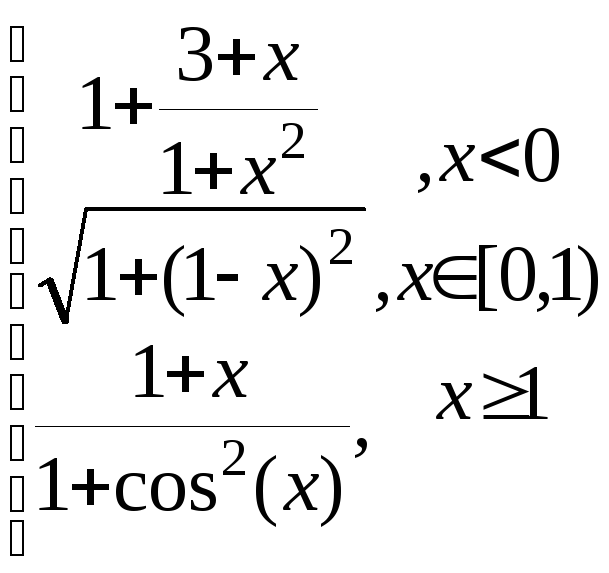

(b) Побудувати в одній системі координат при хє[-2;2] графіки слідуючих двох функцій:

y=5sin(x)-cos(3x)sin(x), z=cos(2x)-2sin³(x).

(c) Побудувати поверхню z=5x²cos²(y)-2y²e^y при x,y[-1,1].

(d) Знайти всі корені рівняння

x³-0,38x²-7,2495x+3,387384=0.

Варіант 15

(а) Побудувати в різних системах координат при хє[-1,7;1,5] графіки слідуючих функцій:

y=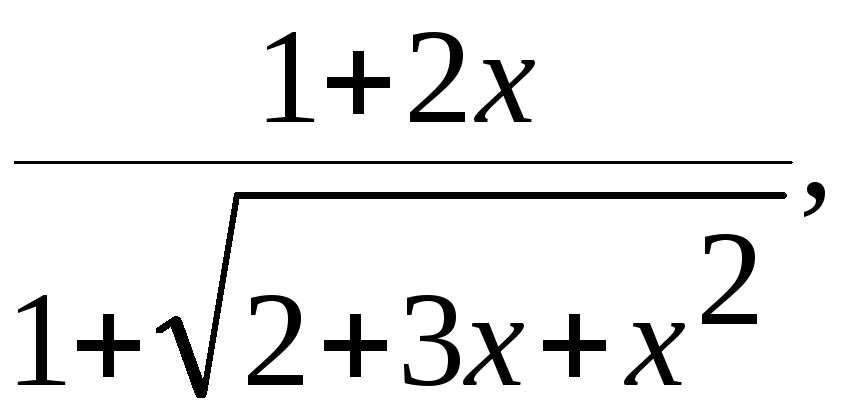 g=

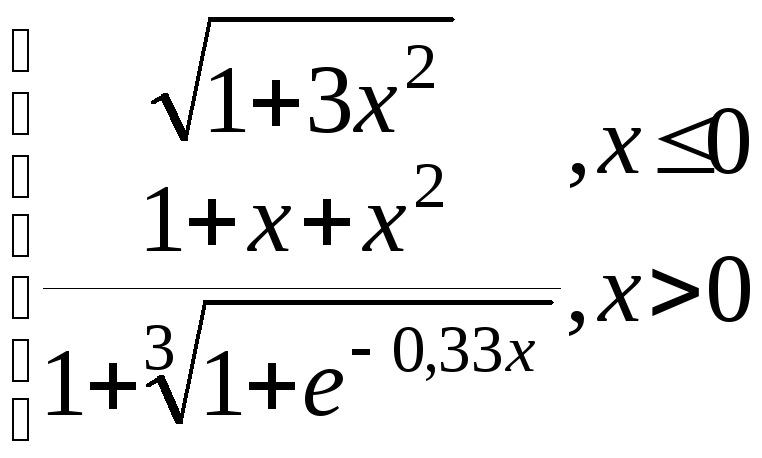
z=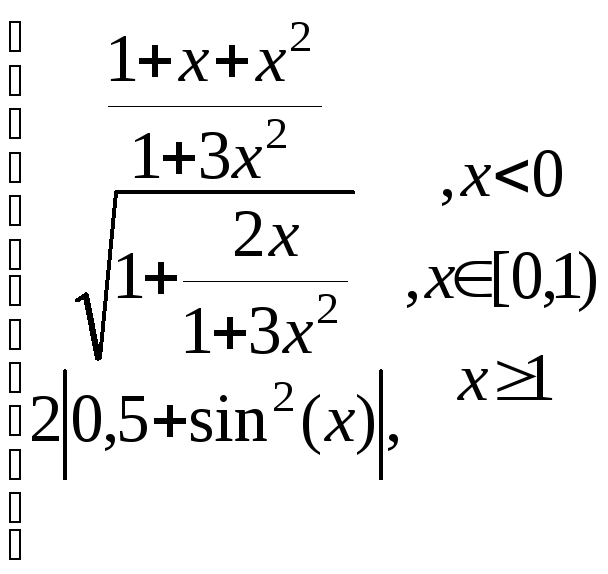

(b) Побудувати в одній системі координат при хє[-2;2] графіки слідуючих двох функцій:

y=3sin(2x)cos(x)—cos²(3x), z=2cos²(2x)-3sin(3x).

(c) Побудувати поверхню при x,y[-1,1]

z=

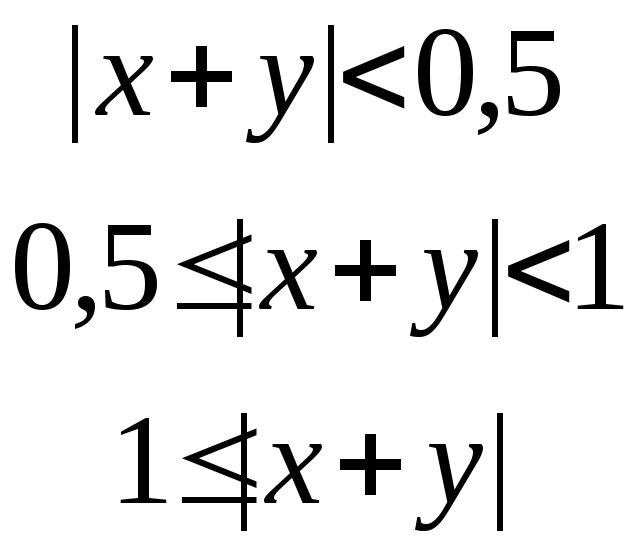
(d) Знайти всі корені рівняння

x³-1,86x²-4,4596x+4,574856=0.

Варіант 16

(а) Побудувати в різних системах координат при хє[-1,7;1,5] графіки слідуючих функцій:

y=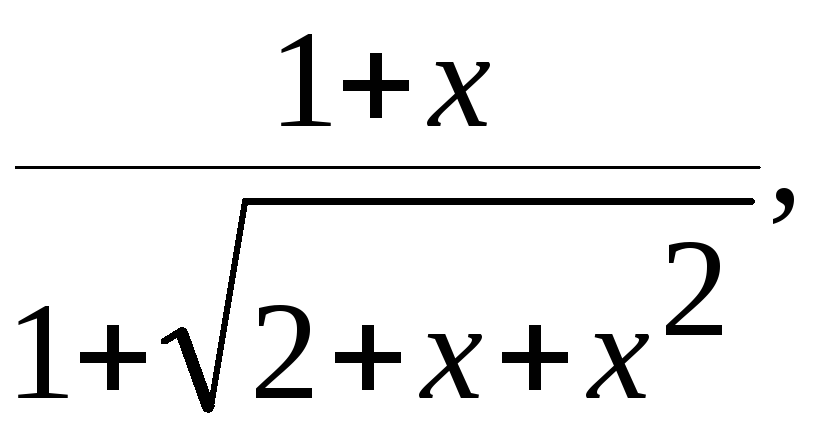 g=

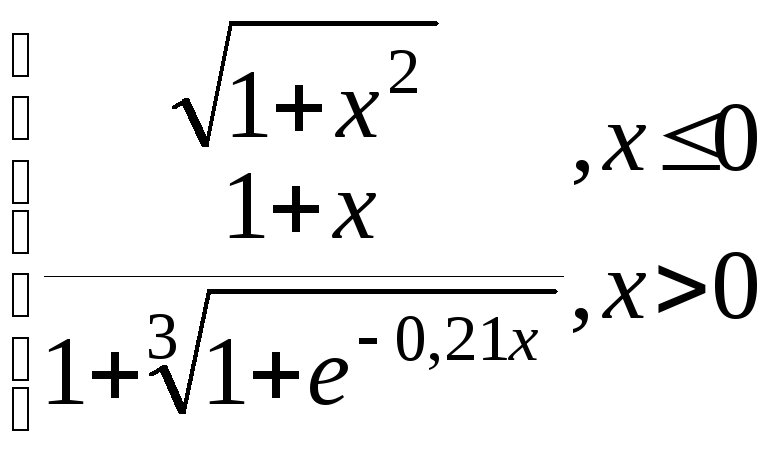
z=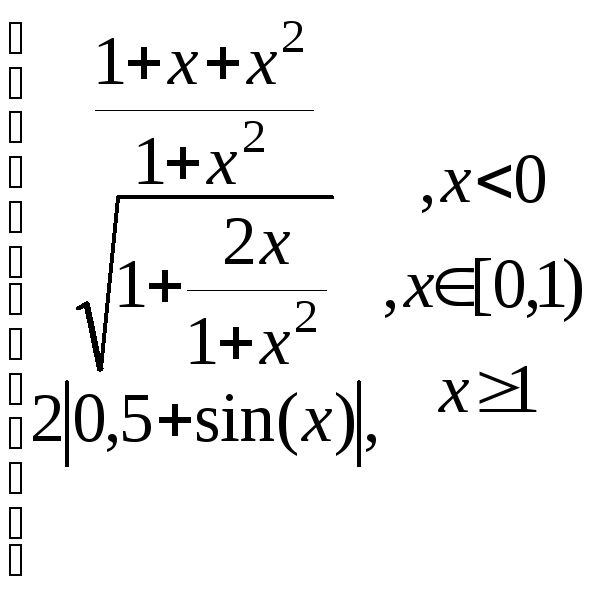

(b) Побудувати в одній системі координат при хє[0;3] графіки слідуючих двох функцій:

y=3sin(3x)cos(2x), z=cos³(4x)sin(x).

(c) Побудувати поверхню z=2e^0,2xx²-2y⁴ при x,y[-1,1].

(d) Знайти всі корені рівняння

x³-0,37x²-2,8669x+1,3253=0.

Варіант 17

(а) Побудувати в різних системах координат при хє[-1,8;1,8] графіки слідуючих функцій:

y= g=

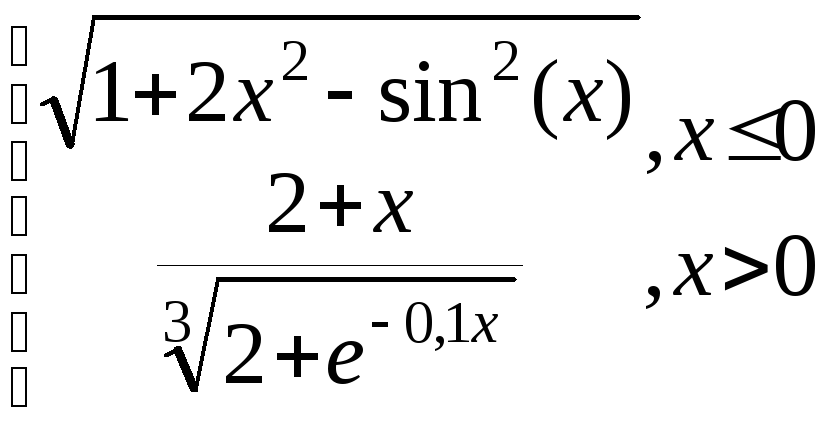
z=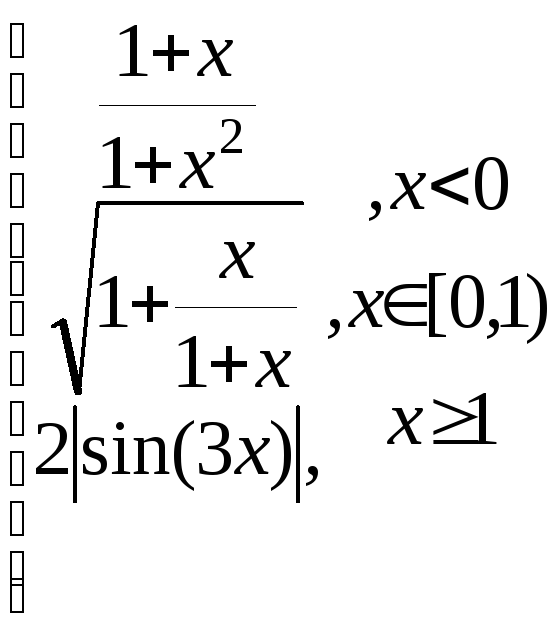

(b) Побудувати в одній системі координат при хє[-3;0] графіки слідуючих двох функцій:

y=2sin(2x)cos(4x), z=cos²(3x)-cos(x )sin(x).

(c) Побудувати поверхню z=x²-2e^0,2yy² при x,y[-1,1].

(d) Знайти всі корені рівняння

x³-0,41x²-5,9412x+3,3345=0.

Варіант 18

(а) Побудувати в різних системах координат при хє[-1,8;1,8] графіки слідуючих функцій:

y= , g=

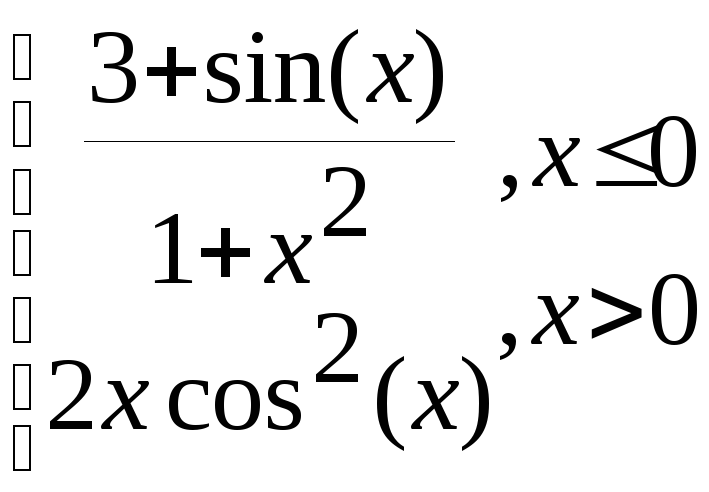
z=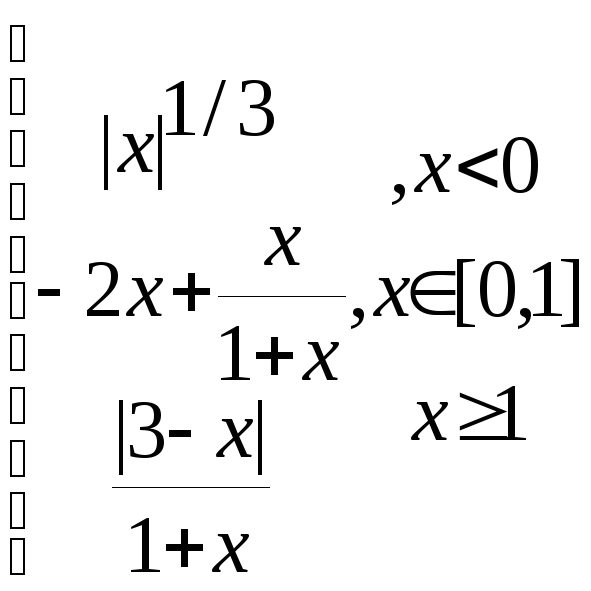

(b) Побудувати в одній системі координат при хє[-3;0] графіки слідуючих двох функцій:

y=2sin²(2x)cos³(4x), z=cos²(3x)-cos³(x )sin(x).