1.17. Напряжения в проводах и тросах, тяжения по ним

в нормальных режимах работы

Расчеты проводов и тросов производятся по методу допускаемых напряжений, нормативные значения которых приведены в табл. Расчеты линий с обычной длиной пролетов (примерно до 800м) осуществляется по напряжению провода (троса) в его низшей точке. Вместе с тем напряжения в точке крепления проводов должны быть не больше 1,05 допускаемого значения для алюминиевых проводов и стальных тросов и 1,10 для сталеалюминевых. В точках крепления на опоре напряжение в проводе (тросе) больше, чем в его низшей точке. При равной высоте расположения точек подвески (см. рис.)

,

где f – стрела провеса провода, м, при удельной нагрузке , Н/(ммм²), и напряжении в низшей точке ,Н/мм².

Комбинированные, в том числе сталеалюминевые, провода рассчитываются по полному тяжению, действующему по проводу, суммарному сечению алюминиевой и стальной частей, эквивалентным модулю упругости, температурному коэффициенту линейного расширения и допускаемому напряжению провода в целом (см. табл.).

Напряжение провода (троса) при климатических условиях, характеризуемых температурой воздухаи удельной нагрузкойопределяется по уравнению состояния провода:

,

где величины с индексом m относятся к известному (исходному) состоянию провода, а с индексом n – к искомому состоянию; l- длина пролета.

Уравнение состояния является неполным кубическим уравнением вида

,

где А=;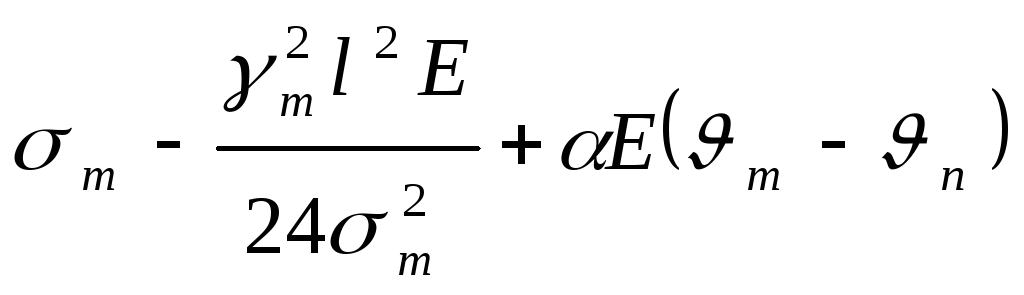

.

Такое уравнение рекомендуется решать методом Ньютона, получая результат с хорошей точностью на третье итерации, по следующей итерационной формуле:

.

Как начальное приближение (нулевые итерации) рекомендуется принимать значения, получаемые по следующим эмпирическим формулам:

если ;

если .

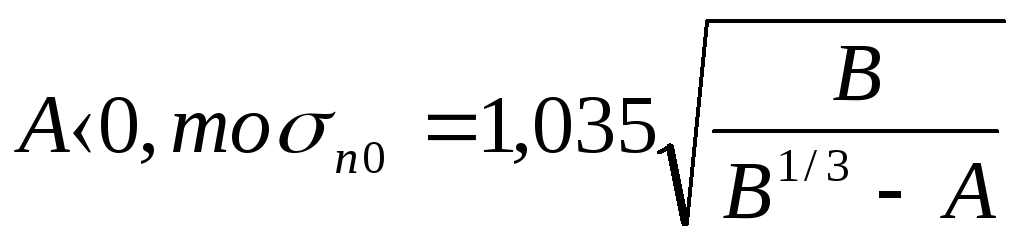18. Стрела провеса и напряжение в материале провода

Провод, закрепленный в двух точках на одинаковой высоте и испытывающий равномерно распределенную нагрузку от собственной массы, массы гололеда и давления ветра, можно рассматривать, как гибкую нить, принявшую форму цепной линии (рис.15-4).

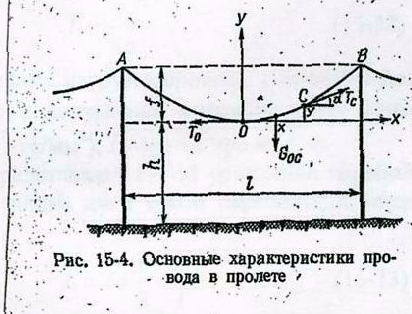
При достаточно больших отношениях длины пролета l к стреле провеса f (что соответствует действительности) кривая провеса провода очень близка к параболе вида:

При совмещении начала координат с наинизшей точкой провеса провода (т.е. полагая h=0) уравнение параболы примет вид:

Исходя из этого уравнения и полагая длину провода в пролете примерно равной длине пролета (L)? Выведем формулу для расчета стрелы провеса провода.

В каждой точке вдоль провода, закрепленного между точками А и В, действует сила тяжения T_i, обусловленная нагрузками на провод и зависящая от стрелы провеса провода.

Вырежем участок ОС с координатами О (0,0) и рассмотрим его равновесие. На отрезок провода в точках О и С действуют постоянные силы тяжения Т_О и Т_С, а также вертикальные нагрузки , гдеg₀ – вертикальная нагрузка провода длиною 1м.

Условия равновесия отрезка будут соблюдены, если сумма проекций всех составляющих сил на оси х и у будет равна нулю, т.е.

или –Т_О+Т_С cos (15-8)

или – g₀x+T_C sin (15-9)

Разделив выражение (15-9) на выражение (15-8), получим

Помня, что tgесть первая производная , можем написать:

, где g₀ и T₀ – постоянные величины, а y – текущая ордината кривой провеса провода:

. (15-10)

Положив в выражении (15-10) x=l/2, получим стрелу провеса провода для пролета

. (15-11)

Выразив вертикальную нагрузку провода g₀ через его удельную нагрузку , а также тяжение провода Т₀ – через напряжение материала провода , получим расчетную формулу для стрелы провеса провода, м:

, (15-12)

где y_x – удельная вертикальная нагрузка провода, соответствующая условиям расчета провода, Н/м³; - напряжение при растяжении в низшей точке провода. Соответствующее тем же условиям расчета, Па (10^-7кгс/мм²); l – длина пролета, м.

Выражение (15-2) представляет собой уравнение параболы с хордой l и стрелой f. Как известно из математики, длина дуги такой параболы, а следовательно, и длина провода в пролете будет:

. (15-13)

Длина провода в пролете отличается от длины пролета менее, чем на 0,1%, т.е. на очень малую величину. Таким образом, сделанное ранее допущение о равномерном распределении нагрузки на по длине провода, а по длине пролета не приводит к заметной погрешности.

Напряжение в материале провода по его длине неодинаково в различных точках пролета. В низшей точке провеса провода оно меньше всего (), а у точек закрепления провода на опоре оно под воздействием вертикальных нагрузок провода на участках ОА или ОВ достигает наибольшей величины (). Для определения этой наибольшей величины служит формула:

. (15-14)

В пролетах нормальной длины разница между иочень мала (не больше 0,3%) и ею обычно пренебрегают, используя для расчетов данные по напряжению в низшей точке провеса провода. Но при очень больших пролетах (порядка 500м и более) необходимо применять формулу (15-14).