4.8. Теорема единственности для внутренней и внешней задач электродинамики.

Уравнения Максвелла являются дифференциальными уравнениями в частных производных, поэтому они допускают множество решений. Из общефизических соображений, очевидно, что если полностью повторять условия опытов, то будем получать одно и то же распространение электромагнитного поля. Для обеспечения единственности решения электродинамических задач электромагнитное поле должно удовлетворять не только уравнениям Максвелла, но также должно удовлетворять ряду дополнительных условий. Они называются условиями единственности решения уравнений Максвелла. Выводы и доказательства формулируются теоремой единственности. Теорема единственности отдельно формулируется двух основных видов задач:

для внутренней и внешней задач электродинамики.

Требуется определить распределение электромагнитного поля внутри поверхности S (внутренняя задача). Определим распространение электромагнитного поля в пространстве, внешнем по отношению к объему V, ограниченному поверхностью S. ().

4.9. Единственность решения внутренних задач.

Внутренние задачи электродинамики имеют единственное решение, если выполняется одно из следующих условий:

1.Если в каждой точке М поверхности S задана проекция вектора на плоскость, касательную к поверхности S в точке М:— "Е" задача.

2. Если в каждой точке M поверхности S задана проекция вектора на плоскость, касательную к поверхности S в точке М:— "Н" задача.

3. Если на части поверхности S в каждой точке задана проекция вектора на плоскость, касательную к S в этой точке, а на другой части плоскости задана проекция векторакасательная к S в точке М:

—"ЕН" задача.

4. Если в каждой точке поверхности S задано соотношение между проекциями векторов ина плоскость, касательную к S в точке М.

4.10. Условия единственности внешних задач электродинамики.

Для обеспечения единственности решения внешних задач электродинамики необходимо выполнение одного из условий 1-4, плюс к этому должно выполнятся одно из условий, описывающее поведение электромагнитного поля при бесконечно удаленных точках (при r®¥).

1. Принцип предельного поглощения () требует, чтобы эта зависимость была, т.е. каждая из составляющих поля должна убывать с увеличением расстояния быстрее, чем. В реальных средах имеются пусть очень малые, но конечные по величине потери, т.е.. Поэтому, в бесконечно удаленных точках, электромагнитное поле равно нулю.

2. Если в среде отсутствуют потери и принцип предельного поглощения не применим, в этом случае векторы электромагнитного поля должны удовлетворять следующим соотношениям:

—условия Зоммерфельда.

Физически эти условия означают, что электромагнитные волны при r®¥ имеют вид сферических волн, расходящихся от источника электромагнитного поля.

Раздел 5. Электродинамические потенциалы гармонического поля.

5.1.Уравнения Гельмгольца.

Практически все задачи электродинамики разделяют на 2 вида:

1. прямые задачи, в которых по заданному распределению сторонних источников необходимо определить соответствующее распределение электромагнитного поля.

2. обратные задачи, в которых по заданному распределению электромагнитного поля надо определить соответствующее распределение сторонних источников.

В этом разделе рассмотрим основные методы решения прямых задач электродинамики применительно для гармонического ЭМ поля и однородных линейных изотропных сред.

Относительно мгновенных значений векторов поля задачи решают очень редко, из-за сложности их определения. Обычно задачи решают для гармонических полей с использованием метода комплексных амплитуд. При решении любых электродинамических задач очень редко используют непосредственно уравнения Максвелла. Обычно уравнения Максвелла стараются свести к известным формам дифференциальных уравнений.

Рассмотрим гармонический электромагнитный процесс. Запишем уравнения Максвелла для комплексных амплитуд:

(1)

(2)

Возьмем ротор от правой и левой части соотношения (1). Получим:

(3)

Воспользуемся известным тождеством:

Из 4-ого уравнения Максвелла: следует, что:

(4)

Подставим (4) и (2) в соотношение (3) и получим: или

(5)

В результате проведенных преобразований мы получили неоднородное дифференциальное уравнение, которое в математической физике называется неоднородным уравнением Гельмгольца. Это уравнение описывает волновые процессы. Векторное дифференциальное уравнение (5) можно записать в виде трех уравнений проекций:

(6)

Аналогичные уравнения можно получить и для вектора напряженности поля.

(7)

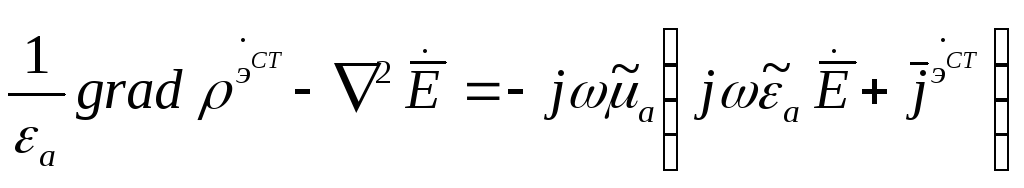
Меняя везде знаки, получим:

(8)

При анализе сред, в которых отсутствуют сторонние источники, неоднородные уравнения (5), (8) преобразуются в однородные:

(9)

Соотношения (5), (8), (9) называются уравнениями Гельмгольца относительно векторов поля.

2. Электродинамические потенциалы для комплексных амплитуд.

Даже уравнения Максвелла, преобразованные к уравнениям Гельмгольца в форме (5),(8), используются при решении электродинамических задач из-за сложной правой части. При решении задач для векторов поля уравнения используются только для полей без сторонних источников. Обычно, если рассматриваемые задачи со сторонними источниками, используют искусственный прием - вводят формальные поля, которые описываются некоторыми функциями, называемыми электродинамическими потенциалами. Для них решают электродинамическую задачу, а соответствующие вектора электромагнитного поля находят, используя уравнения связи между электромагнитными потенциалами и векторами поля.

Получим выражения для электродинамических потенциалов. Для этого запишем уравнения Максвелла:

(1)

(2)

(3)

(4)

Существует следующее векторное тождество:

и (5)

Векторную функцию называютвекторным электрическим потенциалом. Соотношение (5) при известном однозначно определяет вектор. Обратное определение неоднозначно, т.е. при известном векторном полесоотношение(5) определяет неоднозначно. Известно, что. Поэтому, если ввестии, то соотношение(5) не изменится. Поэтому соотношение (5) определяет с точностью до градиента произвольной функции.

Подставим (5) в (2). Получим: или(6)

Воспользуемся вновь тождеством: и.

При этом: (7)

Скалярную функцию называютскалярным электрическим потенциалом. Знак " - " поставлен, чтобы в случае электростатических полей мы получили соотношение, связывающее напряженность электрического поля и электрический потенциал. С помощью соотношений (5) и (7) определили векторы магнитного и электрического полей через два формальных поля: поля векторного электрического потенциала и поля скалярного электрического потенциала. Получим уравнения для их определения. Подставим соотношения (5) и (7) в первое уравнение Максвелла:

Помножим на , раскроеми раскроем скобки.

Формальные поля векторного и электрического потенциалов были введены без ограничений, т.е. это совершенно произвольные функции. Единственное ограничение — это то, что векторное поле электрического потенциала определяется точностью до градиента произвольной функции. Поэтому мы вправе ввести какие-то ограничения. Пусть таким ограничением будет:

(8)

Равенство (8) называется условием калибровки.

А теперь: (9)

Аналогичным образом может быть получено выражение для определения скалярного электрического потенциала. Для этого нужно воспользоваться третьим уравнением Максвелла. Вместо запишем соотношение(7):

Вместо подставим то, чему она равна, используя условие калибровки:

52