ZADAChI2 / Задачи по теме 12 ПриложенияИнтегралов

Задачи по теме «Приложение определенного интеграла»

1. Найти площадь плоской фигуры, ограниченной графиками функций , ,

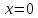
2. Найти площадь фигуры, ограниченной линиями

3. Найти площадь между графиками функций 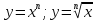(. Вычислить предел этой площади при

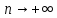
4. Найти площадь плоской фигуры, ограниченной лемнискатой

5. Найти площадь плоской фигуры, ограниченной астроидой 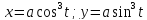(a>0)

6. Найти площадь плоской фигуры, ограниченной параболой и гиперболой . Ответ (Данко 1593)

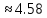
7. Найти объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной кривой 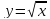и прямой .

8. Найти объем тела вращения 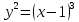, 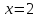Ответ (Данко 1626 )

9. Найти объем тела вращения , .

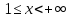10. Найти объем шара радиуса R.

11. Найти длину одного витка винтовой линии ()

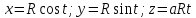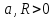12. Найти длину цепной линии 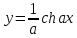при

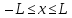
13. Найти длину графика , .

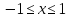14. Найти площадь сферы радиуса R.

15. Найти площадь поверхности параболоида, полученного вращением параболы , (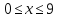) вокруг оси Ох.

16. Найти момент инерции цилиндра массой 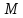и радиуса 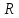относительно его оси.

17. Найти момент инерции шара массой и радиуса 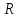относительно диаметра.

18. Найти координаты центра тяжести однородного параболического сегмента, ограниченного линиями , .

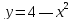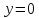19. Найти работу, совершаемую при выкачивании воды из корыта, имеющего форму полуцилиндра, длина которого равна , радиус основания равен 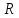. Ответ .

20. Найти силу давления воды на вертикальную стенку в форме полукруга, диаметр которого равен 6 м и он (диаметр) находится на поверхности воды. Плотность воды 1000 кг/м.куб. Ответ 176,4 кН

21. Материальная точка движется по оси Ox и в момент времени 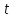ее скорость равна . Известно положение точки в начальный момент: 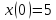. Найти .

22. Найти массу стрежня Ответ (Данко 1678)