ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ

1. Общие определения

Функция двух переменных 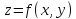сопоставляет каждой точке некоторой области на плоскости число по какому-либо закону. Примеры: 1) – площадь прямоугольника со сторонами . Здесь область задается неравенствами . 2) - расстояние от точки до начала координат. Здесь Р – любая точка, и D – вся плоскость Oxy.

Графиком функции двух переменных называется поверхность в пространстве , состоящая из точек таких, что и пробегает всю область допустимых значений функции

Линия уровня С функции двух переменных задается уравнением . Например, линии уровня функции не пусты лишь, если и представляют из себя концентрические окружности радиуса с центром в начале координат. Линии уровня функции -- пучёк прямых, параллельных прямой

Функция трех переменных 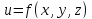сопоставляет каждой точке из некоторого тела число. Например, -- температура тела в точке

Поверхность уровня С функции задается уравнением

2. Предел и непрерывность

Пусть функция определена в окрестности точки .

Определение. Число называется пределом функции при (записываем как ), если для любого ε>0 найдется , что как только

то .

Функция непрерывна в точке если . По-другому это можно сформулировать так: полное приращение функции

стремиться к нулю, если одновременно.

Свойства пределов и свойства непрерывных функций те же самые, что и для функции одной переменной. Алгебраические операции, а также подстановка функции в функцию не выводят за класс непрерывных функций.

3. Частные производные

Частные приращения по и по функции определяются так:

Сумма частных приращений, вообще говоря, не равна полному приращению, по определению равному

Частной производной по называется предел отношения частного приращения по к приращению переменной , если последнее (приращение) стремиться к нулю:

По другому частная производная обозначается как Техника вычисления частных производных такая же, как и «обычных» производных. Найдем частные производные от функции

Аналогично определяются частные производные высших порядков. Производная называется смешанной.

Теорема о равенстве смешанных производных. Две смешанные производные одного порядка и отличающиеся друг от друга лишь порядком дифференцирования равны при условии непрерывности этих производных.

Например,

4. Дифференциал.

1. Определение дифференцируемости

Определение. Функция называется дифференцируемой в точке, если ее полное приращение можно представить в виде суммы линейной функции от и и величины бесконечно малой высшего порядка относительно :

Тогда эта линейная часть называется дифференциалом и обозначается .

Замечание. Нетрудно видеть, что если бесконечно малые величины относительно , то величина есть бесконечно малая высшего порядка по сравнению с . Действительно, величины ограничены по модулю единицей, и произведение б.м. функций на них суть б.м. величины (см. «Введение в анализ»). Отсюда вытекает, что отношение есть б.м. величина и тем самым числитель есть о-малая величина по сравнению со знаменателем. Верно и обратное утверждение – любая представима в виде , где -- бесконечно малые величины.

ТЕОРЕМА 1. Если функция дифференцируема в точке , то существуют частные производные в этой точке и .

ДОКАЗАТЕЛЬСТВО. Полагаем в (1) . Получаем Делим получившееся соотношение на и затем устремляем к нулю:

Аналогично доказывается, что □

Замечание. Взяв 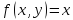находим . Аналогично, . Итак, приращение и дифференциал независимой переменной суть одно и то же. В связи с этим замечанием и теоремой 1 дифференциал приобретает окончательный вид

Пример. Пусть Тогда и

Это функция четырех переменных. Фиксируем точку (1,2). Значение функции в ней равно , а дифференциал равен Пользуясь этим, найдем приближенно значение 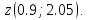Имеем:

(Точное значение равно 2,9525)

Приближенные вычисления, основанные на понятии дифференциала, используют формулу .

2. Достаточное условие дифференцируемости

ТЕОРЕМА 2. Если существуют и непрерывны в окрестности точки , то функция дифференцируема в этой точке.

3. Производная сложной функции

ТЕОРЕМА 3. Пусть --дифференцируемые функции, а имеет непрерывные частные производные в области . Тогда имеет место формула

Уравнение касательной плоскости к графику функции в точк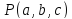е , где имеет вид

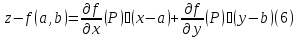
ПРИМЕРЫ 1. Найдем уравнение касательной плоскости к графику функции в точке . Имеем:

откуда по формуле (6) получаем: или .

2. Найдем уравнение касательной плоскости и нормальный вектор к поверхности , заданной уравнением в точке . Имеем:

Отсюда получаем вектор нормали и уравнение касательной плоскости (см. (5)) имеет вид или .

5. Формула Тейлора

Выведем формулу Тейлора функции в точке исходя из формулы Тейлора функции одной переменной:

Здесь -- бесконечно малые величины. Переставляя слагаемые и учитывая, что есть бесконечно малая высшего порядка малости по сравнению с получаем формулу Тейлора функции двух переменных до членов второго порядка включительно:

ОПРЕДЕЛЕНИЕ. Выражение называется вторым дифференциалом функции f в точке P. Это есть квадратичная форма двух переменных.

ПРИМЕР. Разложим по формуле Тейлора функцию в окрестности точки Р(1,1). Считаем:

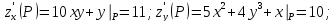
Тогда

Пользуясь этим разложением, вычислим приближенно --

Точное значение функции в точке равно 10.0911

6. Экстремумы

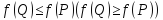Точка называется точкой локального максимума (минимума) функции , если найдется окрестность этой точки такая, что для любой . Локальный экстремум – это либо локальный максимум, либо локальный минимум.

Необходимое условие экстремума. В точке экстремума все частные производные равны нулю (если они существуют). Более того, производная по любому направлению равна нулю в такой точке.

Действительно, если является для функции локальным максимумом, то есть локальный максимум функции одной переменной Применим необходимое условие экстремума функции одной переменной и получим . Это равносильно равенству Аналогично доказываются равенства .

Из формулы вытекает, что производная по любому направлению равна нулю. □

Точка , в которой все частные производные, а значит и производная по любому направлению равны нулю, называется стационарной. Точка O(0,0) для функции является локальным и даже глобальным минимумом. Точка O для функции является локальным и даже глобальным максимумом. Точка O для функции является стационарной, но не экстремальной. Такого рода стационарную точку будем называть седловой, так как по одному направлению, а именно по направлению оси OX , функция z имеет эту точку как точку локального минимума, а по другому направлению – по оси OY , эта же точка будет локальным максимумом.

Пример 1. Найдем все стационарные точки функции . Имеем: и . Приравнивая частные производные к нулю, и исключая из системы, получим Отсюда, учитывая, что в силу ОДЗ, находим и Итак, получили единственную стационарную точку Заметим, что на границе области функция обращается в бесконечность. То же самое верно и при , а также при . Следовательно, минимум достигается в какой-то внутренней точке области .

Перейдем к выводу достаточных условий экстремума функций многих переменных.

ЛЕММА. Квадратичная форма положительно определена, т.е. принимает только положительные значения для всех , если и только если выполнены условия.

В случае

эта квадратичная форма отрицательно определена, т.е. принимает только отрицательные значения при всех .

Квадратичная форма положительно определена, если и только если противоположная форма отрицательно определена. Кроме того, матрица удовлетворяет условиям (1) тогда и только тогда, когда матрица удовлетворяет условиям (2). Отсюда вытекает, что достаточно рассмотреть случай положительно определенной квадратичной формы. Предположим, что неравенства (1) выполнены. Тогда соотношение

полученное путем выделения полного квадрата показывает, что форма положительно определена, ибо и и при этом лишь в том случае, когда .

Наоборот, пусть форма положительно определена. Подставляя в нее получаем, что . Тогда соотношение (3) имеет место и при получаем значение формы равное которое также должно быть положительным.□

Достаточное условие экстремума. Пусть Р – стационарная точка функции , т.е. Обозначим

Если выполнено условие (1), то P – точка локального минимума. Если же выполнено условие (2), то P – точка локального максимума. Если же определитель меньше нуля, то Р -- седловая точка, и экстремума в этой точке нет.

Доказательство. Применим формулу Тейлора и разложим функцию в окрестности точки :

Допустим, что выполнено условие (1). Величина не может изменить знака квадратичной формы при достаточно малых . Отсюда следует, что при таких же достаточно малых . Это и означает, что есть локальный минимум. Аналогично разбирается случай, когда выполняется условие (2). Если же , то из соотношения (3) видно, что квадратичная форма принимает значения разных знаков. Более точно, при 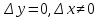ее знак совпадет со знаком , а при 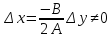ее знак совпадает со знаком , который противоположен знаку . То же самое будет происходить и с приращением при достаточно малых .

Продолжение примера 1. Вернемся к функции . Мы нашли стационарную точку . Вычислим второй дифференциал в этой точке:

и . Это положительно определенная форма, ибо и . Следовательно, -- локальный минимум. Мы знаем большее : -- глобальный минимум в области . Без исследования функции на границе области , нельзя получить этот факт.