10

Тема 16 Линейные уравнения.

Задача Коши для уравнения 2-го порядка. Рассмотрим дифференциальное уравнение 2-го порядка в нормальной форме

Начальным условием для уравнения (1) называется строка чисел .

Теорема существования и единственности. Пусть функция вместе со своими частными производными по второй и третьей переменной непрерывны в некоторой области D пространства , содержащей точку . Тогда существует решение уравнения (1) такое, что

Задача Коши для уравнения (1) как раз и состоит в том, что бы найти решение, удовлетворяющее заданным начальным условиям, т.е. для которого верно (2).

Функция называется общим решением уравнения (1), если

1. для любых констант эта функция есть решение (1)

2. для любых н.у. найдутся константы такие, что есть решение задачи Коши.

Пример. Функция есть общее решение уравнения , а функция есть общее решение уравнения «гармонических колебаний»

Дифференциальное уравнение вида

называют линейным неоднородным уравнением или линейным уравнением с правой частью. Если правая часть равна нулю, т.е. если уравнение имеет вид

то его называют линейным однородным уравнением. Заметим, что для существования и единственности решения задачи Коши достаточно потребовать непрерывности функций . Непрерывность этих функций в дальнейшем предполагается и особо не оговаривается.

Теорема 1. Сумма двух решений однородного уравнения (4) снова будет решением, и произведение решения на число также будет решением.

Доказательство. Пусть -- решения уравнения (4), а -- число. Тогда

откуда следует, что суть также решения уравнения (6)

Теорема 2. Пусть -- общее решение однородного уравнения (4), а -- частное решение неоднородного уравнения (5). Тогда есть общее решение неоднородного уравнения (5).

Доказательство. Пусть -- дифференциальный оператор. Если есть частное решение однородного уравнения (6), т.е. , то

Это доказывает, что есть частное решение неоднородного уравнения (5). Наоборот, предположим, что есть частное решение неоднородного уравнения (5). Тогда, полагая получим

т.е. – решение однородного уравнения (6), причем □

Пример. Рассмотрим уравнение и сопоставим ему однородное уравнение . Будем искать решения этого однородного уравнения в виде степенной функции . Подставляя, получим

Итак, мы нашли два решения 1 и уравнения . По теореме 1 получаем, что пространство решений этого уравнения включает в себя все функции вида . Более того, эта комбинация будет общим решением однородного уравнения . Действительно, какие бы допустимые начальные условия мы ни взяли, всегда можно найти константы и такие, что

Частное решение неоднородного уравнения будем искать также в виде степенной функции . Подставляя, получим

Это дает единственное решение Применяя теорему 2, получаем, что

есть общее решение заданного уравнения. Предположим, что нам дополнительно известны начальные условия . Тогда, составляя систему уравнений

и решая ее, получим , откуда следует, что функция есть решение задачи Коши уравнения 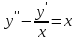c начальными условиями

Основная теорема о структуре пространства решений однородного линейного дифференциального уравнения. Пусть —не пропорциональные решения однородного линейного дифференциального уравнения 2-го порядка. Тогда 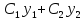есть общее решение этого уравнения.

Доказательство.

1. Линейные однородные уравнения второго порядка с постоянными коэффициентами

Решим дифференциальное линейное однородное уравнение второго порядка с постоянными коэффициентами:

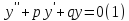
(Здесь p и q – числа). Ищем решение в виде . Эта функция будет решением (1) тогда и только тогда, когда – корень уравнения

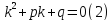
Уравнение (2) называется характеристическим.

Действительно, подставляя в (1) вместо функцию , получаем . Так как экспонента никогда не равна 0, то на нее можно сократить, и мы приходим к квадратному уравнению (2).

Случай 1. .

Тогда уравнение (2) имеет два различных действительных корня и будет Ф.С.Р. уравнения (1). Тем самым -- общее решение дифференциального уравнения (1).

Случай 2. D=0.

Тогда характеристическое уравнение (2) имеет один корень и при этом . Подставляя в (1) функцию , что

и тем самым также будет решением, не пропорциональным решению , Следовательно, общее решение уравнения (1) имеет вид

Случай 3. D<0. Тогда характеристическое уравнение (2) имеет два комплексно сопряженных решения (. Можно проверить, что -- два непропорциональных решения уравнения(1). Отсюда -- общее решение.

Пример. Уравнение имеет характеристическое уравнение вида , у которого есть пара комплексно сопряженных корней . Следовательно, общее решение заданного дифференциального уравнения будет

2. Неоднородные линейные уравнения второго порядка с постоянными коэффициентами

Решаем уравнение

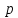где правая часть имеет специальный вид, а и по-прежнему суть числа. Мы применяем теорему, согласно которой общее решение уравнения (3) есть сумма общего решения однородного уравнения (1) и частного решения (обозначим его ) уравнения (3). Так как общее решение однородного уравнения мы научились находить (случаи 1,2,3 выше), то осталось выяснить в каком виде и как находится какое-либо частное решение неоднородного уравнения (3).

Предположим, что есть функция вида (здесь – многочлен степени n).

Случай а) Число не является корнем характеристического уравнения (2).

Тогда частное решение можно найти в виде , где -- многочлен степени n.

Случай б). Число совпадает ровно с одним корнем характеристического уравнения (2).

Тогда частное решение можно найти в виде, где -- многочлен степени n. Приравнивая коэффициенты при одинаковых степенях, после подстановки в уравнение (3), находим коэффициенты многочлена .

Случай в). Число -- двукратный корень характеристического уравнения.

Тогда частное решение можно найти в виде , где -- многочлен степени n,

Подведем итог и сформулируем вид частного решения, применимый сразу для всех трех случаев а), б), в). Для этого определим число – кратность показателя в характеристическом уравнении – число корней (2), с которыми совпадает . По другому, это наибольшее неотрицательное целое число, такое, что делит Возможные значения суть 0, 1 или 2.

Примеры. Для уравнения корни характеристического уравнения суть числа и общее решение однородного есть . Показатель равен 0, ибо . Кратность , ибо 0 не совпадает ни с -1 ни с -3. Частное решение ищем в виде . Подставляя это в исходное уравнение, находим , откуда . Итак 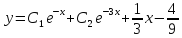-- общее решение.

Уравнение имеет корни , , откуда видим, что кратность и частное решение надо искать в виде . Используя формулу (1), составляем уравнение для многочлена :

Вычисляя производные, получим , откуда и

-- общее решение заданного уравнения.

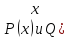Пусть теперь , где ) -- многочлены, наибольшая степень которых равна n.

Случай г) Комплексное число не является корнем характеристического уравнения (3). Тогда частное решение можно найти в виде

где -- многочлены степени n с неопределенными коэффициентами.

Случай д) Комплексное число (b≠ 0) есть корень характеристического уравнения. Тогда частное решение можно найти в виде

где -- многочлены степени n с неопределенными коэффициентами.

Примеры. Частное решение уравнения ищем в виде ибо комплексное число не является корнем уравнения Общее решение имеет вид

Частное решение уравнения ищем в виде ибо комплексное число является корнем уравнения Общее решение уравнения имеет вид

1. Метод вариации постоянных

Решаем неоднородное линейное уравнение

вообще говоря с переменными коэффициентами. Предположим, что нам удалось найти Ф.С.Р. однородного уравнения , тогда общее решение этого уравнения будет .

Решение уравнения (1) ищем в виде , где неизвестные функции, подлежащие определению. Имеем

Положим (*). Тогда, с учетом этого, вычислим вторую производную:

Подставляя и в (1), получим

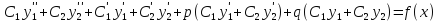
или

Так как , то приходим к уравнению

Вместе с (*), получаем систему, из которой находятся функции интегрированием:

Пример 1. Решим Общее решение однородного уравнения будет иметь вид: . Решение уравнения ищем в виде . Функции находим из системы

откуда

следовательно

Тогда общее решение исходного уравнения будет

Принцип суперпозиции. Частное решение уравнения можно представить в виде суммы , где есть частные решения уравнений .

Пример 2. Решим уравнение Общее решение соответствующего ему однородного уравнения будет Частное решение неоднородного ищем в виде , где есть частное решение уравнения (1н), есть частное решение уравнения (2н). Следовательно, и . Подставляя в уравнение (1н), получим , откуда . Подставляя в уравнение (2н), получим откуда Окончательно, получаем общее решение