Уравнение прямой в пространстве

Прямая может быть задана как пересечение двух плоскостей. В этом случае она задается системой уравнений, определяющих эти плоскости:

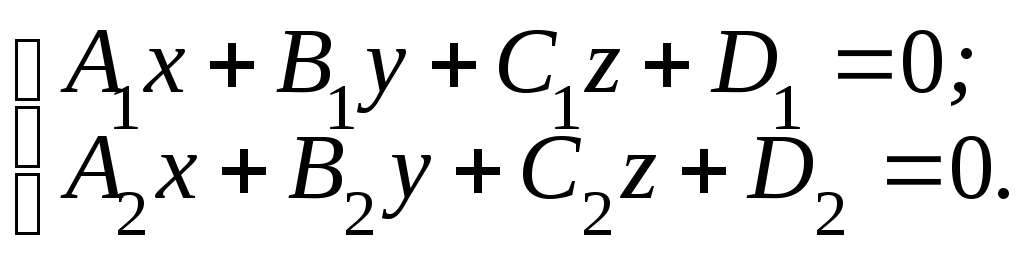(6)

Каноническое уравнение прямой:

. (7)

Здесь М(x₀,y₀,z₀) – точка, через которую проходит прямая, (l, m, n) – направляющий вектор прямой.

Это уравнение на самом деле представляет собой систему двух уравнений, как и в формуле (6). Один или два знаменателя могут быть равны 0, это будет означать, что соответствующие числители приравниваются к 0.

Уравнение прямой, проходящей через две данные точки М₁(x₁, y₁, z₁), М₂(x₂, y₂, z₂):

. (8)

Углом между прямыми в пространстве называют любой из смежных углов, образованных двумя прямыми, проведённых через произвольную точку параллельно данным.

Углом между прямыми в пространстве равен углу между их направляющими векторами.

Если прямые, заданы каноническими уравнениями вида:

и , то

(9)

Косинус угла между плоскостямии

находится по формуле

(10)

В ответе записывается , так как величиной угла между плоскостями называется величина меньшего двугранного угла.

Условие параллельности двух плоскостей:

Условие перпендикулярности двух плоскостей:

.

Пример 9. В пространстве заданы точкиA(3, 2, –1),В(2, –1, 2)С(1, 3, 4),D(4, –5, 5). а) постройте уравнение плоскости (АВС); б) Найдите расстояние от точкиDдо плоскости (АВС); в) постройте уравнение прямойАС; г) постройте уравнение перпендикуляра к плоскости (АВС), проходящего через точкуD.

Решение. а) Воспользуемся формулой (4):

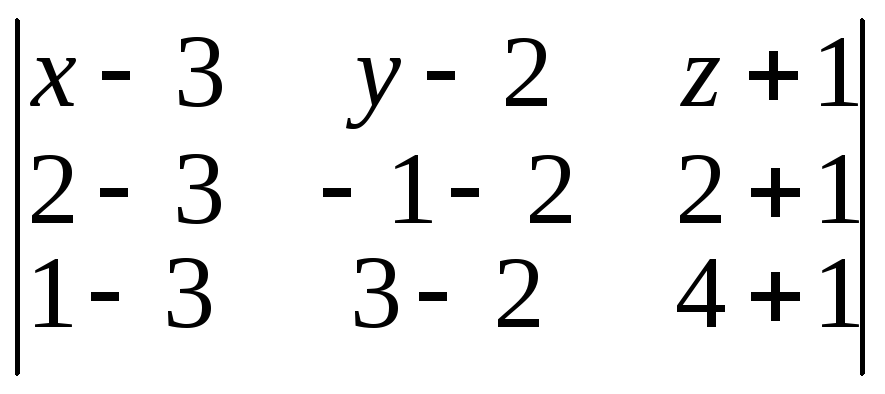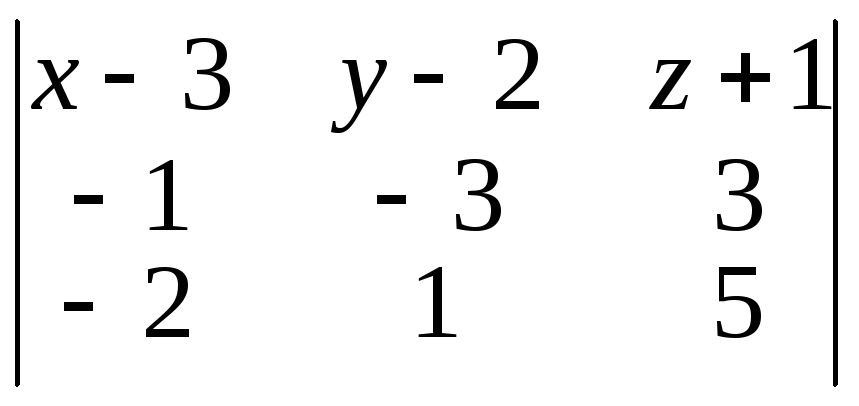= 0;

= 0;

(x– 3)( –15 – 3) – (y– 2)( –5 + 6) + (z+ 1)( –1 – 6) = 0;

–18(x – 3) – (y – 2) – 7(z + 1) = 0;

–18x + 54 – y + 2 – 7z – 7 = 0;

–18x – y – 7z + 49 = 0;

18x + y + 7z – 49 = 0.

б) Воспользуемся формулой (5):

.

в) Воспользуемся формулой (8):

;

.

г) Направляющим вектором перпендикуляра является нормаль к плоскости; из пункта а) это = (18, 1, 7).Воспользуемся формулой (7):

.

У п р а ж н е н и я

1. В пространстве даны точки А(1; 3; 0), B(–1; 2; 1), C(–2; 1; 3), D (2; 2; 1).

а) Постройте уравнение плоскости АВС;

б) Постройте уравнение прямой ВС;

в)Постройте уравнение перпендикуляра, проведенного к плоскости АВСчерез точкуD;

г) Найдите расстояние от точки Dдо плоскостиАВС;

д) Постройте уравнение плоскости, проходящей через точку Dпараллельно плоскостиАВС.

4.Преобразование координат

Ч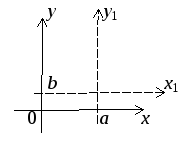асто для определения вида и параметров фигуры, задаваемой уравнением в некоторой системе координат, бывает удобно перейти к другой системе координат. Это может упростить уравнение.

Простейшее преобразование – это параллельный перенос координатных осей. Пусть новые координатные осиx₁ иy₁имеют в старых координатах уравненияx = a, y = b. Тогда новые координатные оси выражаются через старые формуламиx₁=x – a, y₁=y – b, а старые через новые формуламиx=x₁+ a, y=y₁+ b. Например, уравнение окружности с центром в точкеА(a, b) и радиусомrв старых координатах имеет вид (x – a)²+ (y – b)² =r², а в новых x₁²+y₁² =r².

Другой вид преобразований системы координат – это поворот координатных осей вокруг начала координат на угол (угол отсчитывается против часовой стрелки). Формулы перехода от старой системы к новой задаются уравнениями

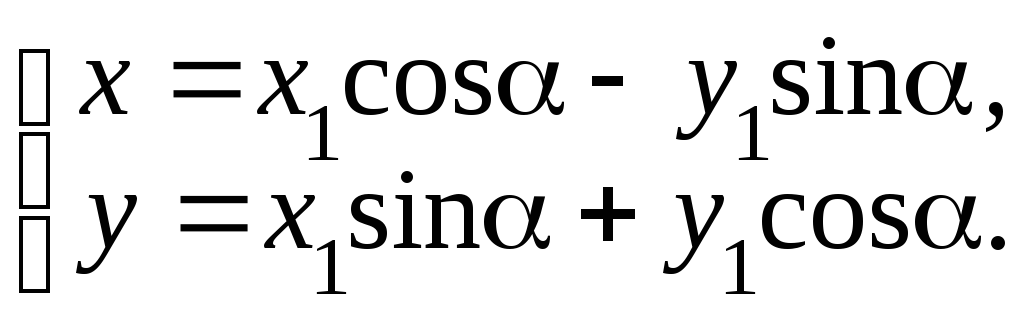
Формулы перехода от новой системы к старой задаются уравнениями

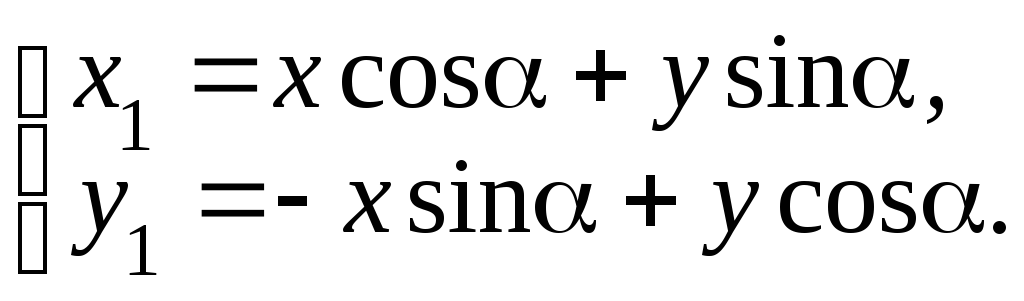
Можно использовать и косоугольную систему координат, в которой оси расположены под произвольным углом и длины единичных отрезков по осям абсцисс и ординат различны. В такой системе прямые линии и многие другие фигуры задаются уравнениями тех же типов, что и в прямоугольной, но параметры уравнений изменяются; становится весьма проблематично определять расстояния и углы. Но использование косоугольной системы координат позволяет упрощать преобразование уравнений в тех случаях, когда требуется определить только тип фигур, задаваемых этими уравнениями. Преобразование координат производится по формулам

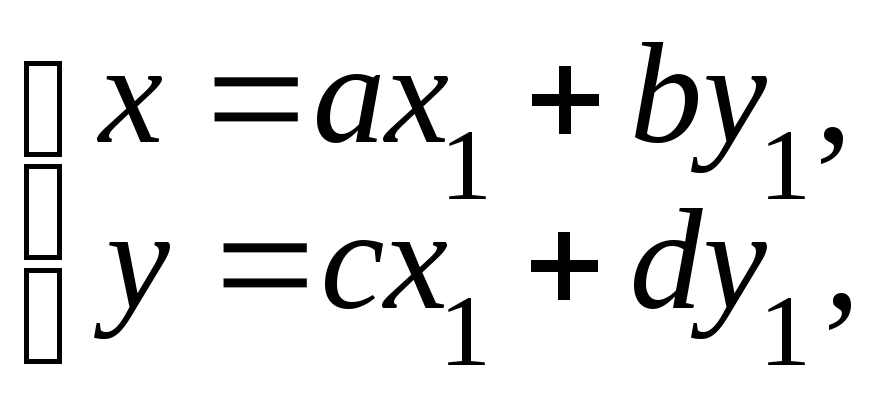
где ad – bc0.

С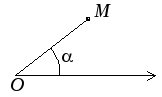овершенно другой вид системы координат, отличный от декартовой, – этополярная система координат. Она задается точкой (полюсом)Ои полярной осью – лучом, выходящим из полюса. Положение любой точкиМна плоскости задается углом, который лучОМобразует с полярным лучом, и радиус-векторомr– длиной отрезкаОМ. Эти два параметра полностью определяют положение точкиМ. При этом радиус-вектор определяется однозначно, а угол с точностью до периода 2: этот период соответствует полному обороту вокруг полюса, приводящему к тому же направлению. Например, уравнение окружности с центром в полюсе и радиусомRв полярной системе имеет видr = R.

От декартовой к полярной системе координат можно перейти по формулам x=rcos,y=rsin. Обратный переход производится с помощью формул

r=;