
- •1.Прямые на плоскости
- •Уравнение прямой на плоскости
- •Дополнительные формулы.
- •У п р а ж н е н и я
- •2.Векторная геометрия
- •Скалярное произведение
- •Векторное произведение
- •Свойства векторного произведения:
- •Смешанное произведение
- •Свойства смешанного произведения.
- •У п р а ж н е н и я
- •3.Прямые и плоскости в пространстве Уравнение плоскости
- •Уравнение прямой в пространстве
- •У п р а ж н е н и я
- •4.Преобразование координат
- •5.Кривые второго порядка
- •Гипербола
- •Парабола
- •Определение вида кривой второго порядка
- •У п р а ж н е н и я
Свойства векторного произведения:
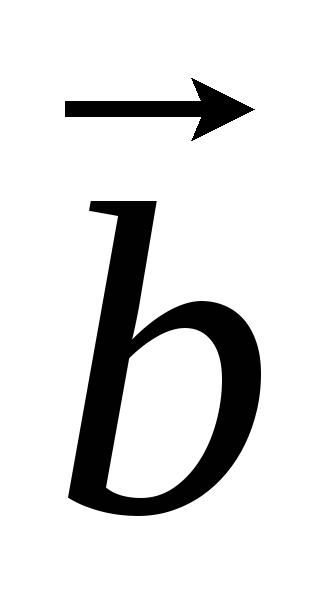
 = –
= –
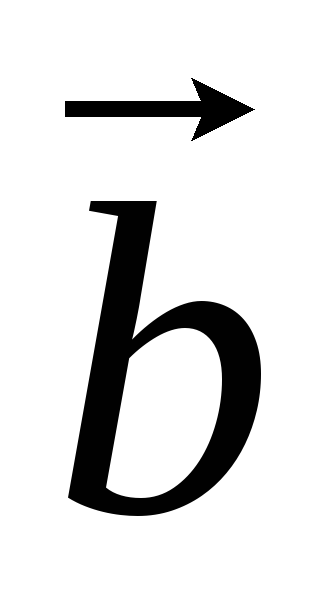 (антикоммутативность).
(антикоммутативность).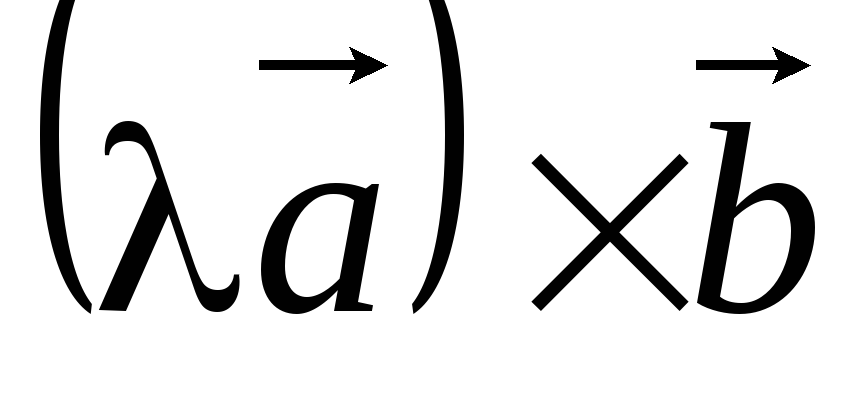 =
=
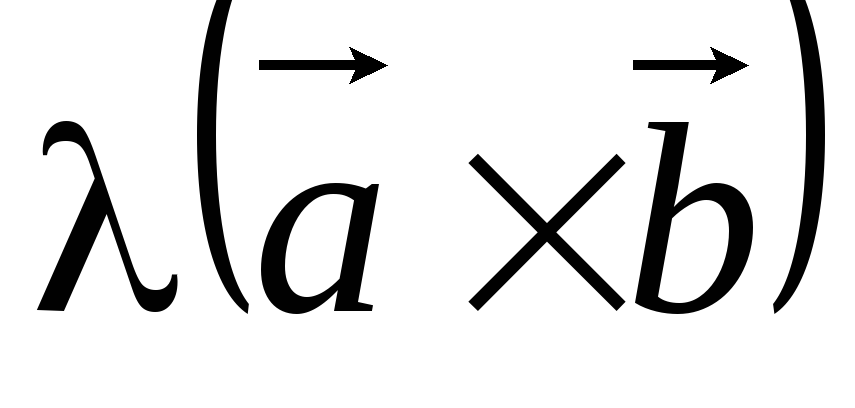 .
.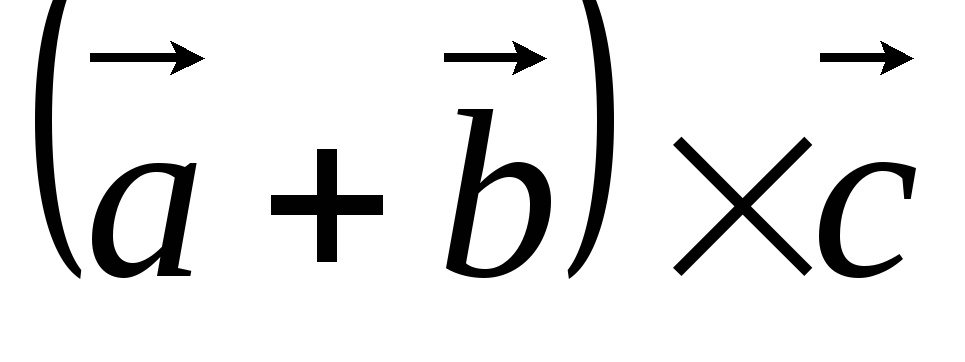 =
=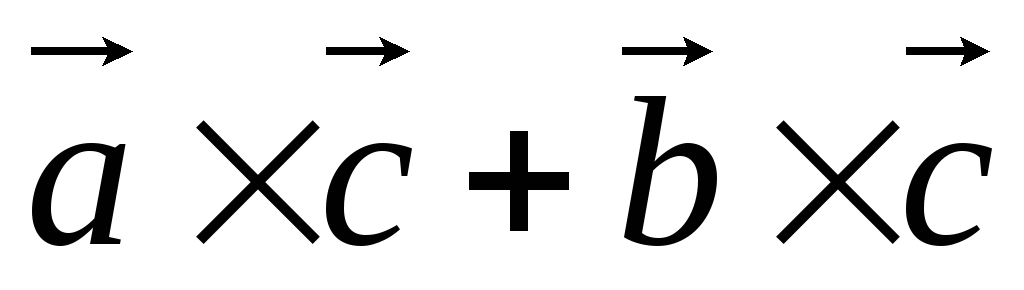 .
.Критерий коллинеарности векторов:
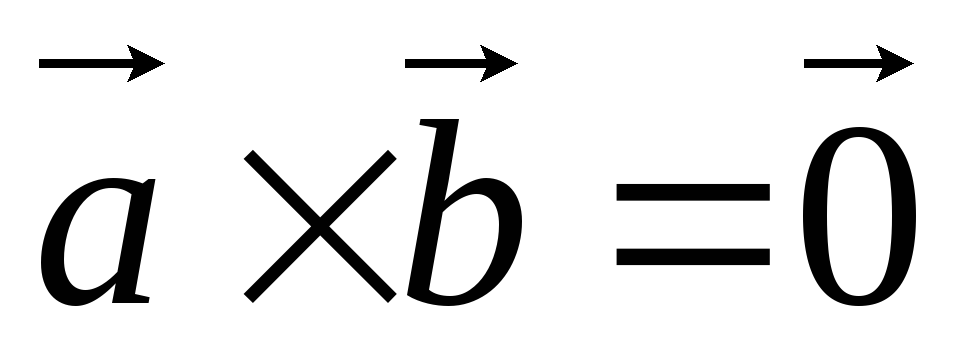 .
.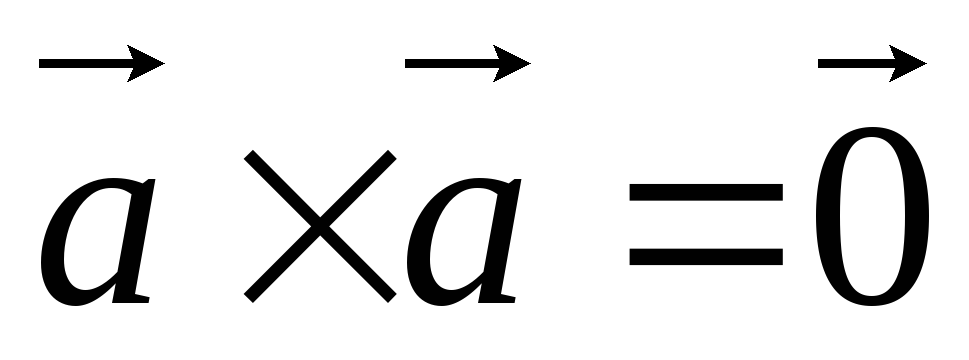 .
.Геометрический смысл векторного произведения: площадь параллелограмма, стороны которого задаются векторами
 и
и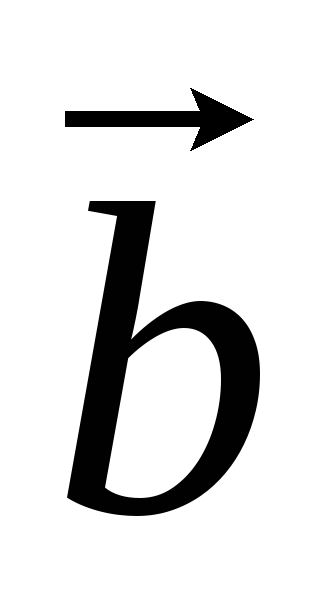 ,
равна модулю их векторного произведения:
,
равна модулю их векторного произведения: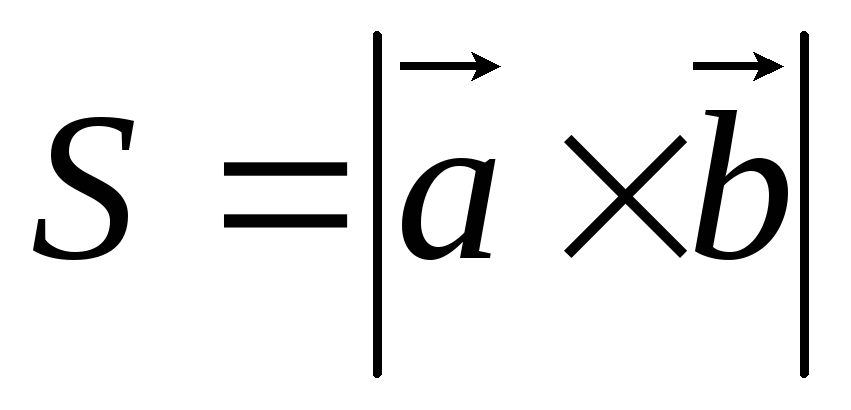 .
.Если
 = (a1,a2,a3),
= (a1,a2,a3),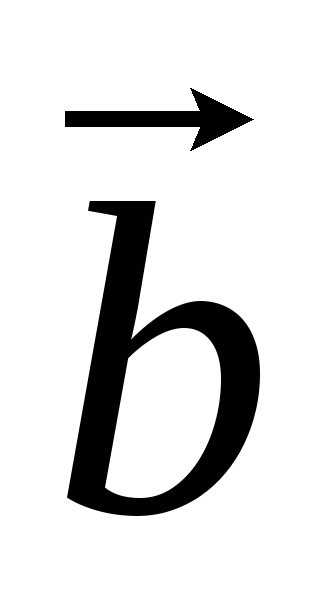 = (b1,b2,b3), причем
базисные векторы образуют правую
тройку, то
= (b1,b2,b3), причем
базисные векторы образуют правую
тройку, то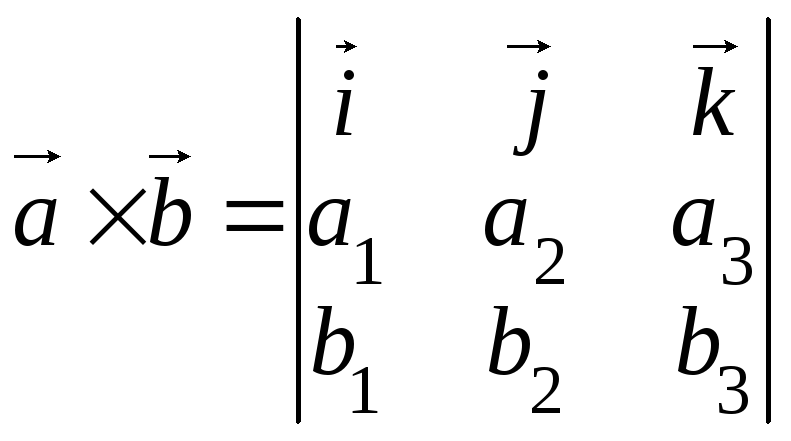 .
.
Пример 6. Найти
векторное произведение векторов![]() = (2, –1, 3), и
= (2, –1, 3), и![]() = (3, 2, –2).
= (3, 2, –2).
Решение. По свойству (7) получаем
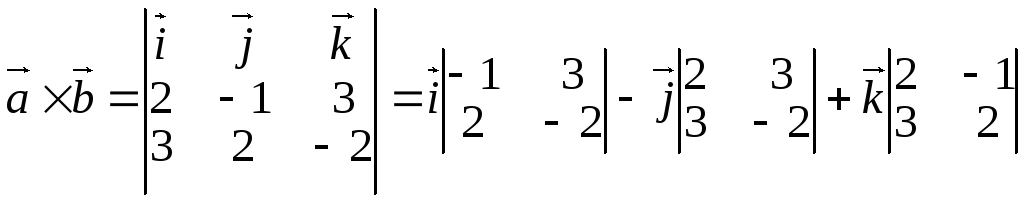 =
=
=
![]() (2
– 6) –
(2
– 6) –![]() (–4
– 9) +
(–4
– 9) +![]() (4
+ 3) = –4
(4
+ 3) = –4![]() + 13
+ 13![]() + 7
+ 7![]() = (–4, 13, 7).
= (–4, 13, 7).
Пример 7. Найти площадь параллелограммаABCD, если заданы координаты вершинA(3, 2, 0),C(2, –1, 2)D(1, 3, –4).
Решение.
Изобразим параллелограммABCDна рисунке, чтобы понять, какие векторы
задают стороны параллелограмма. Так
как заданы точкиA,
C, D,то естественно использовать векторы
Так
как заданы точкиA,
C, D,то естественно использовать векторы![]() и
и![]() (хотя направление векторов не имеет
значения, можно взять противоположные
векторы):
(хотя направление векторов не имеет
значения, можно взять противоположные
векторы):
![]() = (3 – 1, 2 – 3, 0 + 4) =
(2, –1, 4);
= (3 – 1, 2 – 3, 0 + 4) =
(2, –1, 4);
![]() = (2 – 1, –1 – 3, 2 + 4)
= (1, –4, 6);
= (2 – 1, –1 – 3, 2 + 4)
= (1, –4, 6);
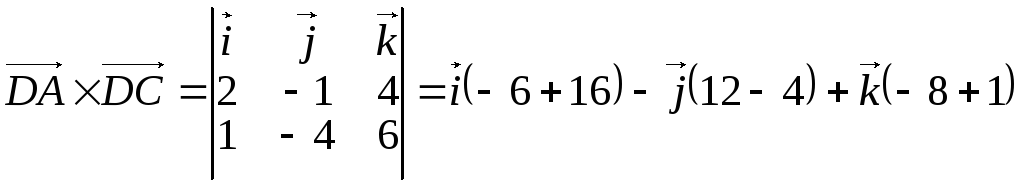 = (10, –8, –7);
= (10, –8, –7);
![]() .
.
Смешанное произведение
Смешанным
произведениемвекторов![]() ,
,![]() ,
,![]() называется число (
называется число (![]()
![]() )
)![]() .
.
Свойства смешанного произведения.
Операции векторного и скалярного произведения можно переставить местами, то есть (

 )
) =
= (
(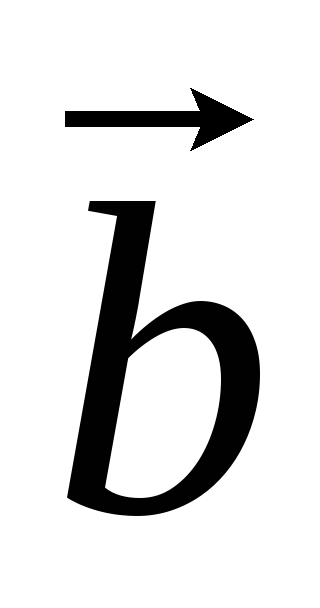
 ),
поэтому смешанное произведение
обозначают просто
),
поэтому смешанное произведение
обозначают просто
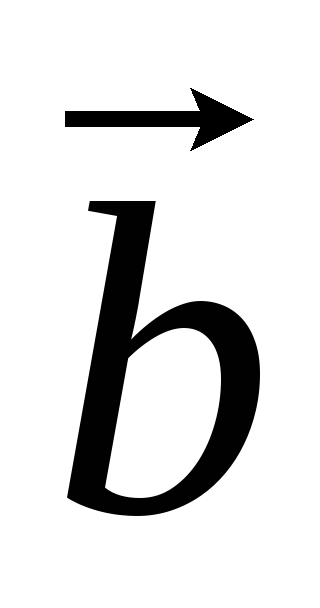
 .
.Циклическая перестановка сомножителей не меняет смешанное произведение:

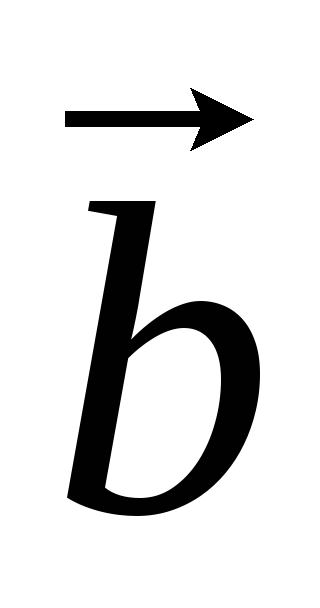
 =
=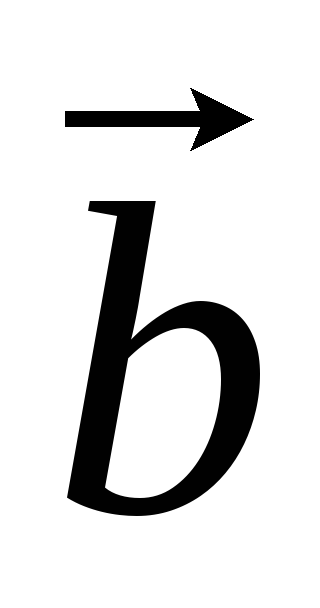

 =
=

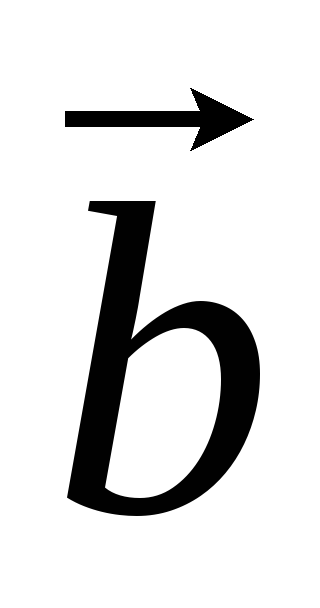 .
.Перестановка двух сомножителей меняет знак смешанного произведения:

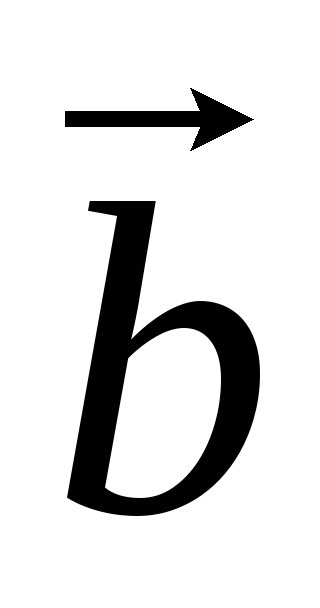
 = –
= –

 = –
= –

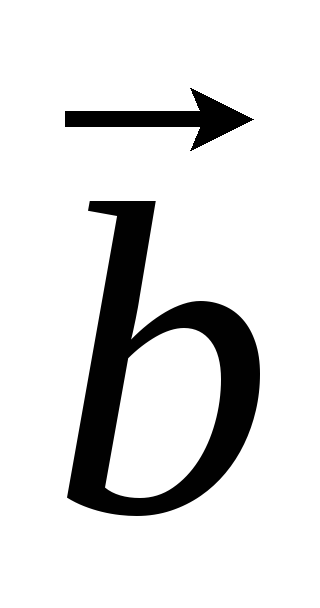 = –
= –
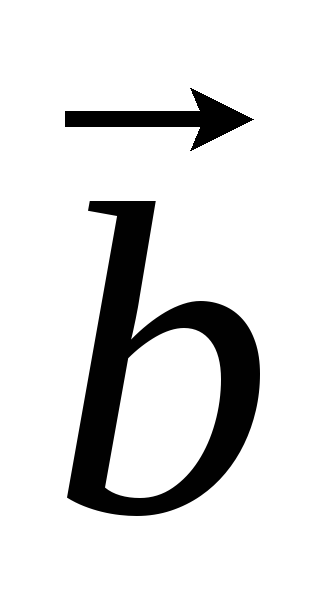
 .
.Геометрический смысл смешанного произведения: объем параллелепипеда, ребра которого задаются векторами
 ,
,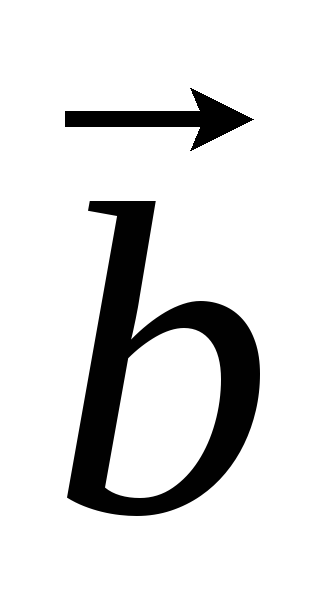 и
и ,
равен
,
равен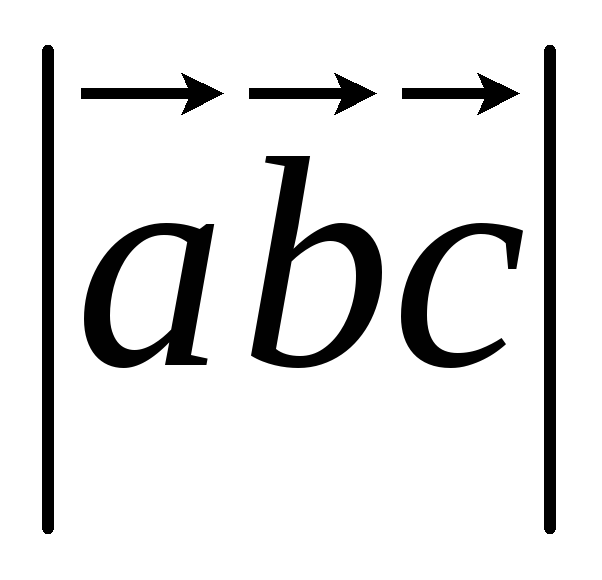 .
.Критерий ориентации тройки векторов
 ,
,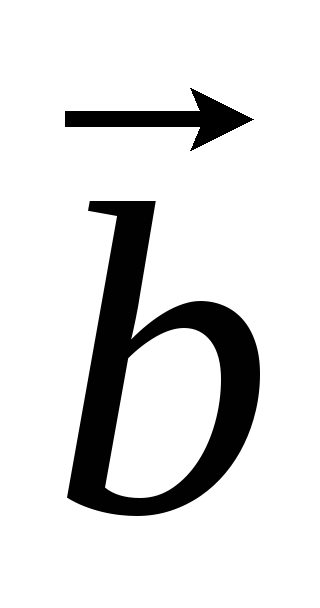 ,
, :
тройка правая, если
:
тройка правая, если
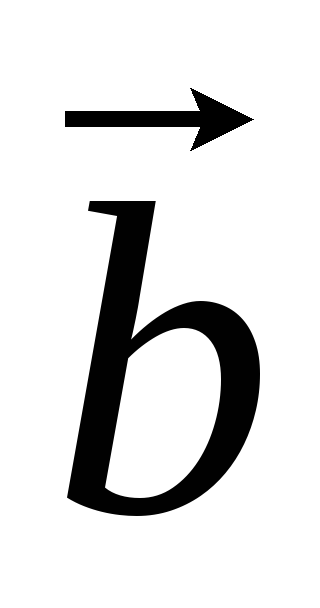
 > 0, и тройка левая, если
> 0, и тройка левая, если
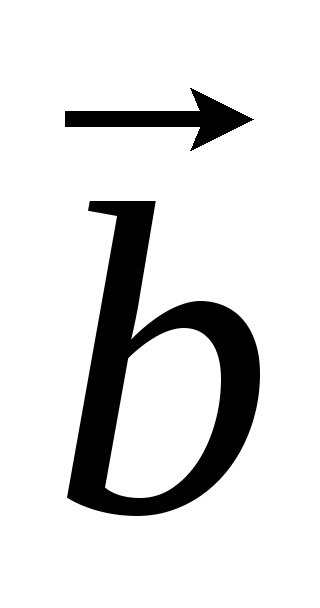
 < 0.
< 0.Критерий компланарности: векторы
 ,
,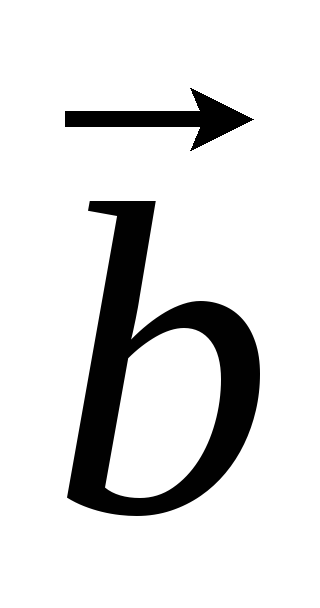 ,
, компланарны тогда и только тогда, когда
компланарны тогда и только тогда, когда
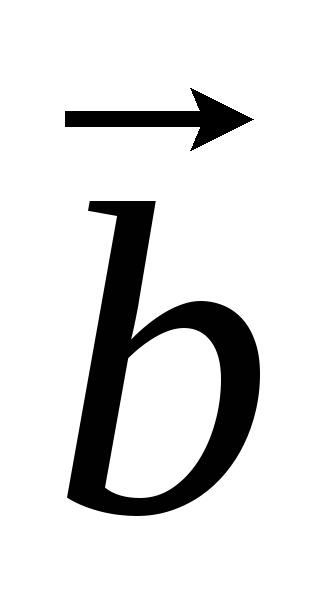
 = 0.
= 0.Если
 = (a1,a2,a3),
= (a1,a2,a3),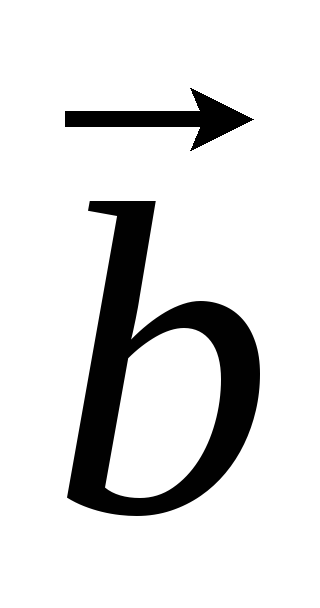 = (b1,b2,b3),
= (b1,b2,b3), = (c1,c2,c3), причем
базисные векторы образуют правую
тройку, то
= (c1,c2,c3), причем
базисные векторы образуют правую
тройку, то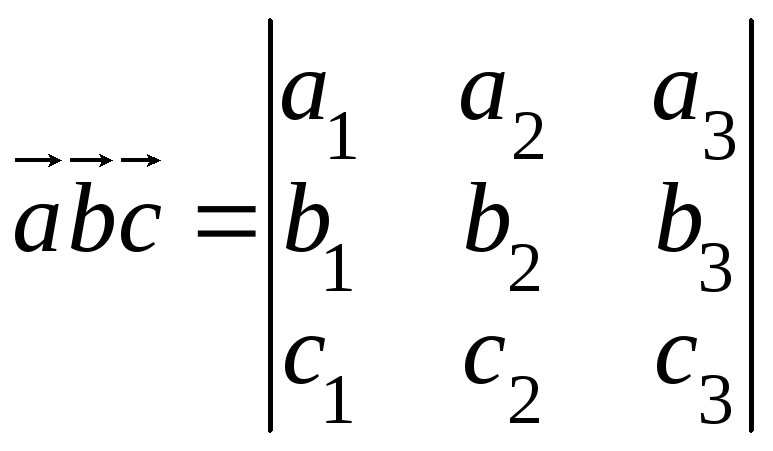 .
.
П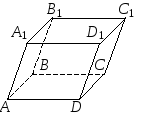 ример
8.Найти объем параллелограммаABCDA1B1C1D1,
если заданы координаты вершинA(3,
2, 0),C(2, –1, 2)D(1,
3, –4),C1(4, 5, 7).
ример
8.Найти объем параллелограммаABCDA1B1C1D1,
если заданы координаты вершинA(3,
2, 0),C(2, –1, 2)D(1,
3, –4),C1(4, 5, 7).
Решение.
Изобразим параллелепипедABCDA1B1C1D1
на рисунке (не стараясь согласовывать
положение вершин с их координатами),
чтобы понять, какие векторы задают ребра
параллелепипеда. Так как заданы точкиA, C,
D, C1,
то естественно использовать векторы![]() ,
,![]() и
и![]() :
:
![]() = (3 – 1, 2 – 3, 0 + 4) =
(2, –1, 4);
= (3 – 1, 2 – 3, 0 + 4) =
(2, –1, 4);
![]() = (2 – 1, –1 – 3, 2 + 4)
= (1, –4, 6);
= (2 – 1, –1 – 3, 2 + 4)
= (1, –4, 6);
![]() = (4 – 2, 5 + 1, 7 – 2) =
(2, 6, 5).
= (4 – 2, 5 + 1, 7 – 2) =
(2, 6, 5).
Тогда
![]()
![]()
![]() =
=
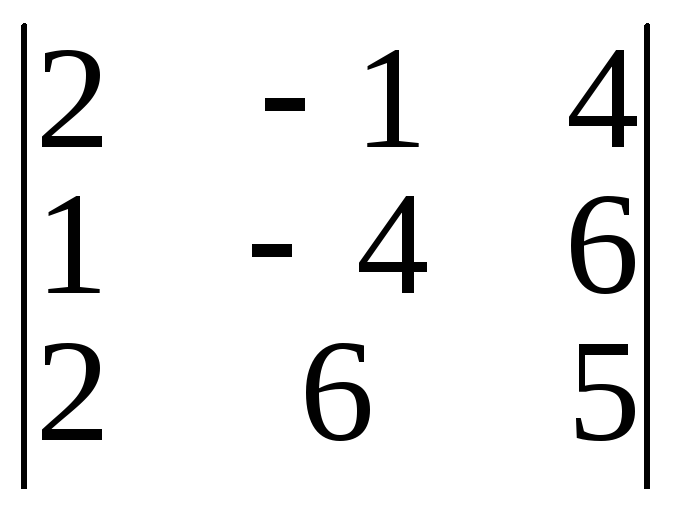 = 2(–20 – 36) – 1(5 – 12) + 4(6 + 8) = –49;
= 2(–20 – 36) – 1(5 – 12) + 4(6 + 8) = –49;
V= 49.
У п р а ж н е н и я
1.Найдите косинус углаСтреугольникаАВС, если заданы координаты вершинА(1; –3; 2), B(1; 0; –2), С(3; 1; 3).
2.Упараллелепипеда ABCDA1B1C1D1 заданы координаты вершин А(1; 3; 0), B(–1; 2; 2), D(3; 2; –2), В1(0; 7; 1). Найдите:
а) объем параллелепипеда;
б) площадь грани ABCD.
3.Прямые и плоскости в пространстве Уравнение плоскости
Общее уравнение плоскости:
Ax + By + Cz + D= 0. (1)
Коэффициенты этого
уравнения определяются не однозначно,
а с точностью до пропорциональности.
![]() не равны нулю одновременно.
не равны нулю одновременно.
Нормалью, илинормальным векторомк плоскости называется любой вектор, ортогональный к этой плоскости.
Вектор, нормальный к плоскости, заданной уравнением (1), это вектор
![]() = (A,
B, C). (2)
= (A,
B, C). (2)
Уравнение
плоскости, проходящей через заданную
точку М(x0,
y0,
z0)
и имеющей нормаль ![]() = (A, B,
C):
= (A, B,
C):
A(x – x0)+ B(y – y0) + C(z – z0) = 0. (3)
Уравнение плоскости, проходящей через три данные точки М1(x1, y1, z1), М2(x2, y2, z2), М3(x3, y3, z3):
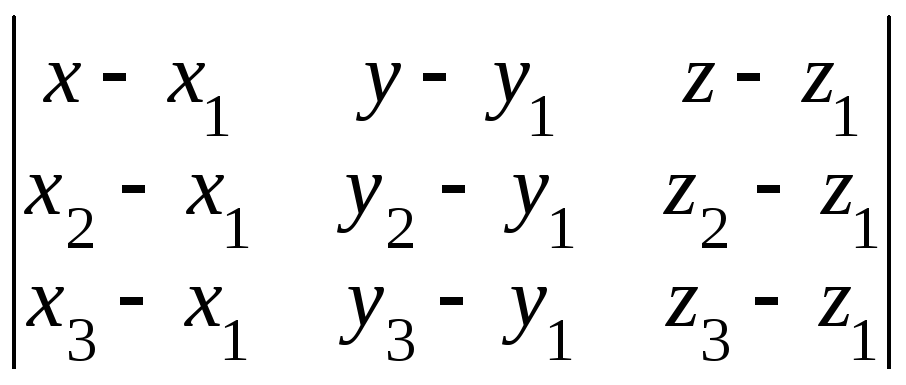 =
0. (4)
=
0. (4)
Расстояние от точки М(x0, y0, z0) до плоскости Ax + By + Cz + D = 0:
![]() . (5)
. (5)
Если плоскость
задана своим общим уравнением
![]() ,
то для координат всех точек, лежащих по
одну сторону от неё
,
то для координат всех точек, лежащих по
одну сторону от неё![]() ,
а для координат всех точек, лежащих по
другую сторону от неё
,
а для координат всех точек, лежащих по
другую сторону от неё![]() .
.
Взаимное расположение двух плоскостей, заданными своими общими уравнениями
Пусть даны плоскости
![]() и
и
![]()
|
Расположение плоскостей |
Условие |
|
Пересекаются |
Ранг матрицы
|
|
Параллельны |
Ранг матрицы
Ранг матрицы
|
|
Совпадают |
Ранг матрицы
|

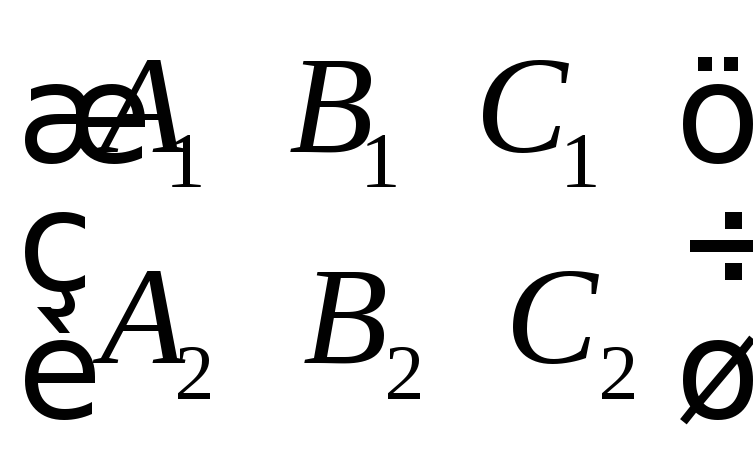 равен 2
равен 2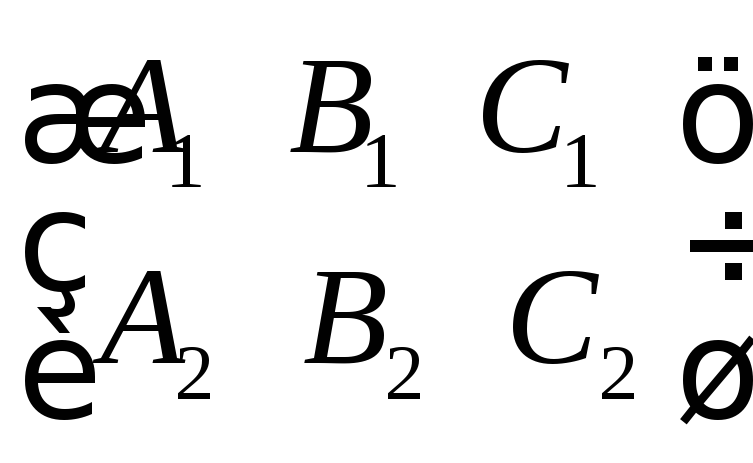 равен 1
равен 1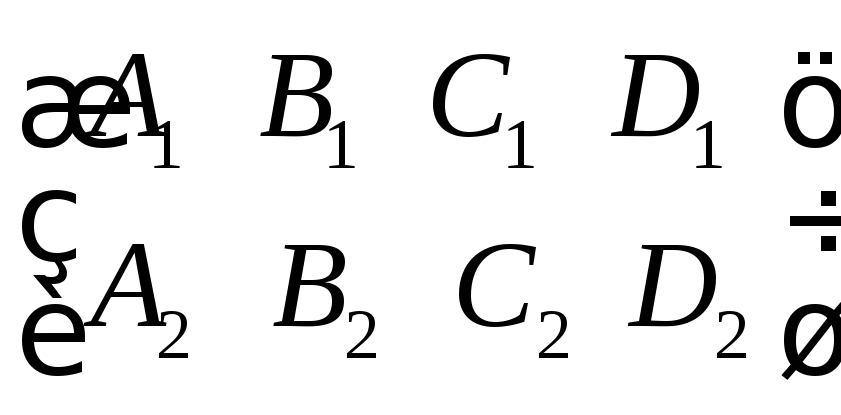 равен 2
равен 2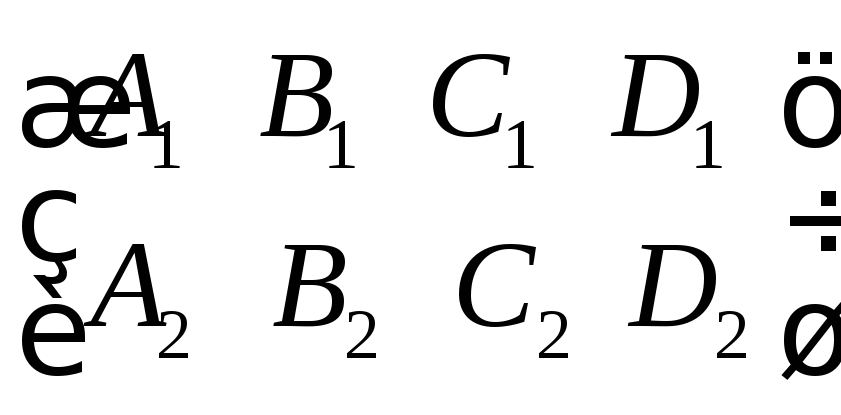 равен 1
равен 1