
- •3.1. Властивості ступенів і коренів
- •Підкореневий вираз розкладемо на прості множники:
- •3.2. Дії з радикалами
- •3.3. Обчислення ірраціональних виразів
- •3.4. Оцінки для радикалів
- •Відповідь
- •4.1. Загальні відомості про рівняння
- •4.2. Рівняння першого степеня з одним невідомим
- •Відповідь
- •4.3. Рівняння другого степеня з одним невідомим
- •4.4. Задачі на використання властивостей дискримінанта
- •4.5. Використання формул Вієта
- •4.6. Розміщення коренів квадратного рівняння
- •Відповіді
- •4.7. Алгебраїчні рівняння вищих степенів та їхні властивості
- •Застосування теореми Гаусса
- •4.9. Рівняння, що зводяться до квадратних рівнянь
- •2. Рівняння вигляду
- •3. Рівняння виду
- •4. Рівняння вигляду
- •Зворотні (симетричні) рівняння
- •Однорідні рівняння
- •4.10. Метод Кардано для розв’язання кубічного рівняння
- •4.11. Уведення параметра замість сталого коефіцієнта
Відповідь
1.
![]()
![]() ;
;
2.
![]()
![]() ;
;
3.
![]()
![]() ;
;
4.
![]()
![]() ;
;
5.
![]()
![]() ;
;
6.
![]()
![]() ;
;
7.
![]()
![]() ;
;
8.
![]()
![]() ;
;
![]()
9.
![]()
![]()
![]() при
при
![]() ;
;
10.
При яких значеннях параметра
![]() для довільного дійсного значення
для довільного дійсного значення
![]() знайдеться хоча б одне дійсне значення
параметра
знайдеться хоча б одне дійсне значення
параметра
![]() ,
таке що задана система рівнянь
,
таке що задана система рівнянь
![]()
![]()
матиме принаймні один розв’язок.
4.3. Рівняння другого степеня з одним невідомим
Алгебраїчне рівняння другого степеня з одним невідомим
![]() (1)
(1)
називається також квадратним рівнянням.
Рівняння виду
![]()
називається зведеним квадратним рівнянням і має розв’язок
![]() .
.
Для рівняння (1) розв’язок можна подати у вигляді
![]() .
.
Для
коренів
![]() зведеного квадратного рівняння
справджується формула Вієта
зведеного квадратного рівняння
справджується формула Вієта

Цей результат випливає з тотожності
![]() .
.
Корені
квадратного рівняння (1) дійсні і різні
при
![]() ,
кратні при
,
кратні при
![]() і не є дійсними при
і не є дійсними при
![]() .
Якщо
.
Якщо
![]() ,
то многочлен
,
то многочлен
![]()
з
дійсними коефіцієнтами
![]() набуває значень лише одного знака. При
набуває значень лише одного знака. При
![]() многочлен
многочлен
![]() набуває значень одного знака, за винятком
однієї точки — кратного кореня рівняння
(1), де многочлен
набуває значень одного знака, за винятком
однієї точки — кратного кореня рівняння
(1), де многочлен
![]() набуває нульового значення.
набуває нульового значення.
Приклад. Знайти розв’язок рівняння
![]() .
.
При
 рівняння має один розв’язок
рівняння має один розв’язок
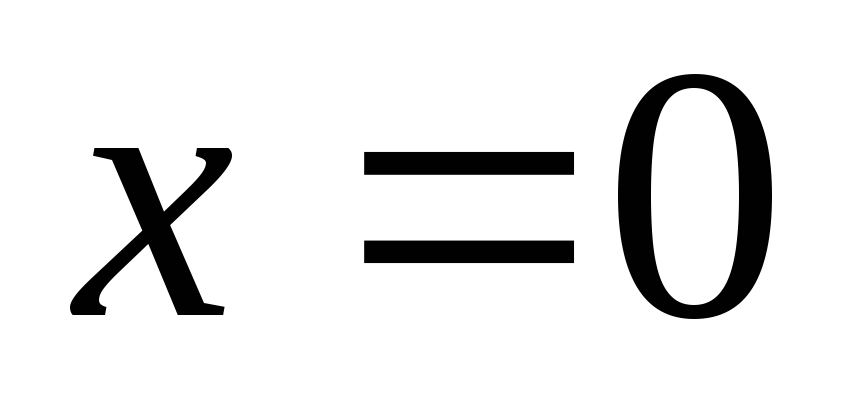 .
.
При
![]() знаходимо дискримінант
знаходимо дискримінант
![]() ,
,
а отже, рівняння має два розв’язки
![]() .
.
Приклад.
Розв’язати рівняння з параметром
![]()
![]() ,
якщо
,
якщо
![]() ,
,
![]() .
.
Виконавши відповідні перетворення, дістанемо квадратне рівняння
![]() , (2)
, (2)
дискримінант якого
![]() .
.
При
![]() ліва частина рівняння (2) тотожно дорівнює
нулю, а тому його розв’язком є будь-яке
значення
ліва частина рівняння (2) тотожно дорівнює
нулю, а тому його розв’язком є будь-яке
значення
![]() .
.
При
![]() обидві частини рівняння (2) можна поділити
на
обидві частини рівняння (2) можна поділити
на
![]() ,
знайшовши два корені:
,
знайшовши два корені:
![]() . (3)
. (3)
За
умови
![]() маємо
маємо
![]() .
.
Розв’язавши
рівняння
![]() при
при
![]() ,
дістанемо розв’язок
,
дістанемо розв’язок
![]() .
Остаточно доходимо таких висновків.
.
Остаточно доходимо таких висновків.
1.
При
![]() рівняння не має розв’язків.
рівняння не має розв’язків.
2. При
![]() рівняння має довільний розв’язок
рівняння має довільний розв’язок
![]() .
.
3.
При
![]() рівняння має єдиний розв’язок
рівняння має єдиний розв’язок
![]() .
.
4.
При
![]() рівняння має дворазові розв’язки
рівняння має дворазові розв’язки
![]() .
.
5.
При
![]() рівняння має комплексні розв’язки.
рівняння має комплексні розв’язки.
6.
При
![]() рівняння має два різні розв’язки
виду (3).
рівняння має два різні розв’язки
виду (3).
Приклад. Розв’язати рівняння
![]() з
параметром
з
параметром
![]() .
.
Якщо
 ,
то дане рівняння стає лінійним.
Розв’язуючи рівняння
,
то дане рівняння стає лінійним.
Розв’язуючи рівняння
 ,
знаходимо
,
знаходимо
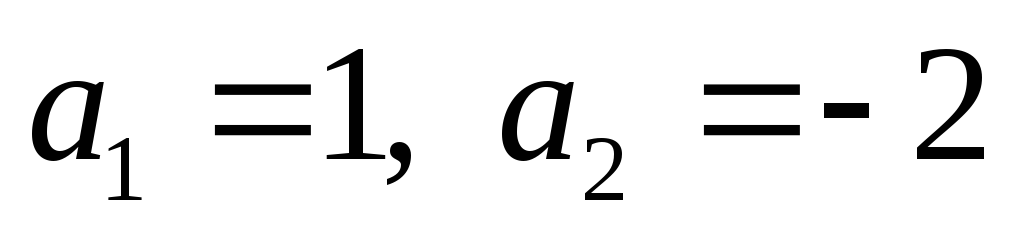 .
.
При
![]() рівняння має єдиний розв’язок
рівняння має єдиний розв’язок
![]() .
.
При
![]() рівняння має розв’язок
рівняння має розв’язок
![]() .
.
При
![]() знаходимо дискримінант
знаходимо дискримінант
![]() ,
,
а далі й корені рівняння
![]() .
.
Приклад. Розв’язати рівняння
![]() .
.
Передусім доходимо висновку, що
 .
.
При цьому рівняння зводиться до вигляду
![]() .
.
Знаходимо дискримінант цього рівняння
![]() .
.
При
![]() виконуються умови
виконуються умови
![]() .
При
.
При
![]() ,
,
![]() знаходимо розв’язок рівняння
знаходимо розв’язок рівняння
![]() . (4)
. (4)
Якщо
![]() ,
то рівняння має єдиний розв’язок
,
то рівняння має єдиний розв’язок
![]() .
Перевіримо виконання умови
.
Перевіримо виконання умови
![]() ,
яка набирає вигляду нерівностей
,
яка набирає вигляду нерівностей
![]() .
.
Остаточно доходимо таких висновків.
1.
Якщо
![]() ,
то рівняння має єдиний розв’язок
,
то рівняння має єдиний розв’язок
![]() .
.
2.
При
![]() рівняння розв’язків не має.
рівняння розв’язків не має.
3.
При
![]() рівняння має єдиний розв’язок
рівняння має єдиний розв’язок
![]() .
.
4.
Якщо
![]() ,
,
![]() ,
то рівняння має два розв’язки виду (4).
,
то рівняння має два розв’язки виду (4).
4.4. Задачі на використання властивостей дискримінанта
Якщо
дискримінант
![]() ,
то квадратне рівняння
,
то квадратне рівняння
![]()
не має дійсних коренів. Через це квадратний тричлен
![]()
не
змінює свого знака при
![]() і має знак коефіцієнта
і має знак коефіцієнта
![]() або коефіцієнта
або коефіцієнта
![]() .
.
Приклад.
Для яких значень параметра
![]() виконується нерівність
виконується нерівність
![]() ?
?
Необхідною і достатньою умовою правильності нерівності є виконання системи умов
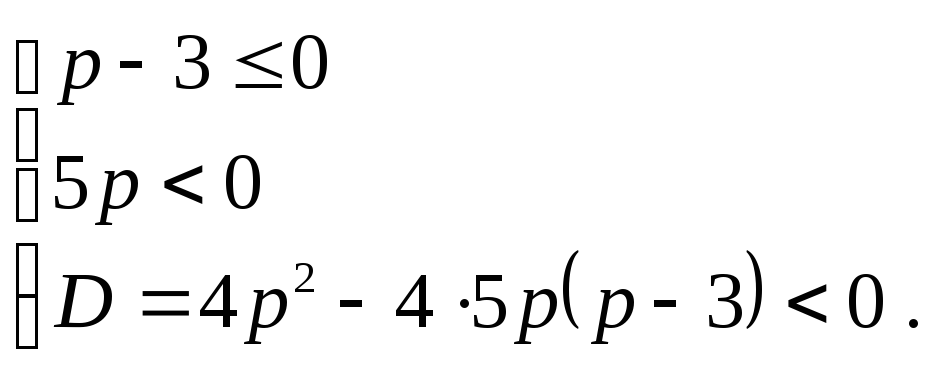
Розв’язуючи
цю систему нерівностей, знаходимо
відповідь:
![]() .
.
Приклад.
При яких значеннях параметра
![]() нерівність
нерівність
![]()
виконується
для будь-якого значення
![]() ?
?
Приходимо до системи нерівностей

яка
має розв’язок
![]() .
.
Приклад.
Знайти всі значення параметра
![]() ,
при яких нерівність
,
при яких нерівність
![]()
виконується
для пари будь-яких чисел
![]() ,
таких що
,
таких що
![]() .
.
Якщо
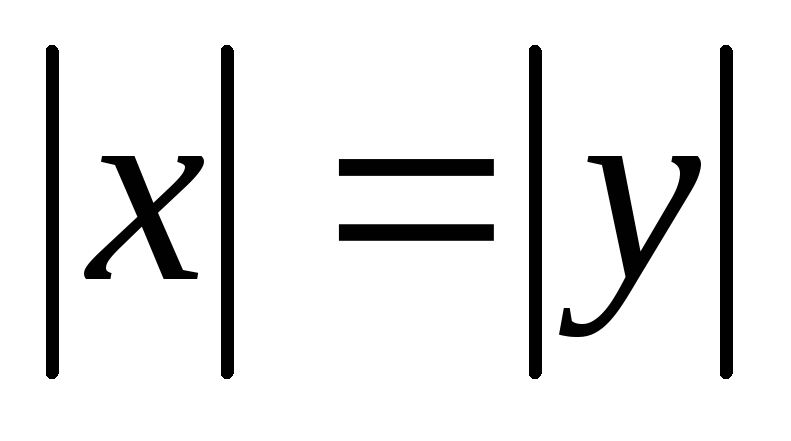 ,
то
,
то
 .
Приходимо до системи нерів-
ностей
.
Приходимо до системи нерів-
ностей
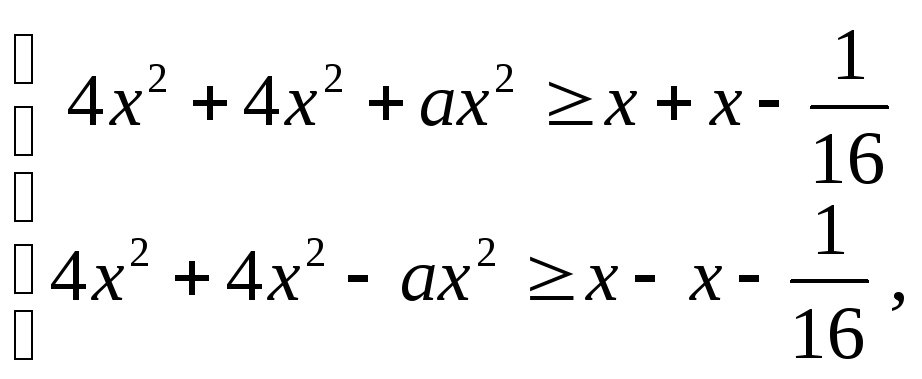
яку можна записати у вигляді

Приходимо
до системи нерівностей для параметра
![]() :
:

Ця
система має розв’язок
![]() .
.
