
- •3.1. Властивості ступенів і коренів
- •Підкореневий вираз розкладемо на прості множники:
- •3.2. Дії з радикалами
- •3.3. Обчислення ірраціональних виразів
- •3.4. Оцінки для радикалів
- •Відповідь
- •4.1. Загальні відомості про рівняння
- •4.2. Рівняння першого степеня з одним невідомим
- •Відповідь
- •4.3. Рівняння другого степеня з одним невідомим
- •4.4. Задачі на використання властивостей дискримінанта
- •4.5. Використання формул Вієта
- •4.6. Розміщення коренів квадратного рівняння
- •Відповіді
- •4.7. Алгебраїчні рівняння вищих степенів та їхні властивості
- •Застосування теореми Гаусса
- •4.9. Рівняння, що зводяться до квадратних рівнянь
- •2. Рівняння вигляду
- •3. Рівняння виду
- •4. Рівняння вигляду
- •Зворотні (симетричні) рівняння
- •Однорідні рівняння
- •4.10. Метод Кардано для розв’язання кубічного рівняння
- •4.11. Уведення параметра замість сталого коефіцієнта
3.3. Обчислення ірраціональних виразів
За допомогою властивостей коренів можна спрощувати й обчислювати ірраціональні вирази.
Приклад. Обчислити вираз
 .
.
Виконаємо послідовно дії:
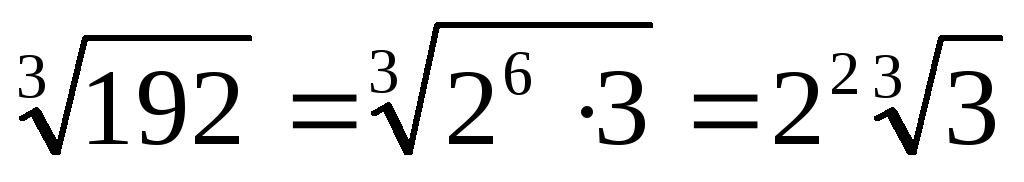 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.
Приклад. Обчислити вираз:
![]()
Виконаємо дії.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Часто використовується формула подвійного радикала:
![]() (8)
(8)
Приклад. За формулою (8) знаходимо:
![]() .
.
![]() .
.
Приклад.
Обчислити вираз
![]()
За формулою (8) знаходимо:


Остаточно дістаємо:
![]() .
.
Аналогічно обчислюються кубічні корені. Маємо:
![]() .
.
Підносимо обидві частини рівності до куба:
![]() .
.
Порівнюючи
вирази при
![]() ,
дістаємо однорідну систему рівнянь:
,
дістаємо однорідну систему рівнянь:
![]() .
.
Поділивши
рівняння почленно, приходимо до рівняння
для
![]() :
:
![]() .
.
Приклад. Обчислити значення радикала
![]() .
.
Після піднесення до куба рівняння приходимо до системи рівнянь:
![]() .
.
Поділивши
почленно перше рівняння на друге,
дістанемо рівняння для
![]() :
:
![]() .
.
За
схемою Горнера знаходимо корінь
![]() .
.
Із
системи рівнянь і рівняння
![]() знаходимо
знаходимо
![]()
![]() .
Отже,
.
Отже,
![]() .
.
Приклад.
Обчислити
![]() .
.
Візьмемо
 .
Підносячи обидві частини рівняння до
куба, дістаємо
.
Підносячи обидві частини рівняння до
куба, дістаємо

 ,
звідки випливає система рівнянь
,
звідки випливає система рівнянь
![]()
Система
рівнянь має очевидний розв’язок
![]() .
.
Тому
![]() .
Обчислюємо радикал
.
Обчислюємо радикал

Остаточно
маємо
![]() .
.
Приклад.
Обчислити
![]() .
.
Оскільки
 ,
то
,
то
 .
Далі маємо:
.
Далі маємо:
![]()
![]() .
.
Отже,
![]() .
.
Приклад.
Обчислити вираз
![]() .
.
Піднесемо рівняння до куба, скориставшись рівністю

 .
.
Дістали
для
![]() кубічне рівняння
кубічне рівняння
![]() ,
або
,
або
![]() ,
,
має
корені
![]() .
.
У
множині дійсних чисел маємо корінь,
![]() .
.
3.4. Оцінки для радикалів
Якщо
![]() то
то
![]() ,
або
,
або
![]() .
(1)
.
(1)
Цю нерівність можна використовувати для доведення нерівностей, що містять радикали.
Приклад.
Довести, що
![]() .
.
Піднісши нерівність до шостого степеня, дістанемо очевидну нерівність
![]() .
.
Можна перетворювати радикали до одного й того самого показника степеня:
![]() .
.
Оскільки
![]() ,
то
,
то
![]() .
.
Приклад.
Оцінимо
![]() .
.
Оскільки
 ,
то
,
то
 .
Отже,
.
Отже,
 .
.
При
перетворенні нерівностей можна
використовувати символ V, розуміючи під
ним знаки «![]() »,
«
»,
«![]() »,
чи «
»,
чи «![]() ».
».
Приклад.
Яке число більше
![]() чи
чи
![]() .
.
 ,
,
![]() .
.
Оскільки
![]() ,
то
,
то
![]() .
.
Розглянемо деякі класичні нерівності, які широко застосовуються в математиці.
Наведемо нерівність Коші
![]() (2)
(2)
і загальнішу нерівність
![]() .
(3)
.
(3)
Нерівність Коші-Буняковського:
![]() .
(4)
.
(4)
При
![]() дістаємо нерівність
дістаємо нерівність
![]() .
.
Якщо
![]() ,
то маємо оцінку
,
то маємо оцінку
![]() .
.
Приклад.
При
![]() маємо оцінку
маємо оцінку
![]() .
.
Наближене
значення
![]() обчислюють за формулою
обчислюють за формулою
![]() .
(5)
.
(5)
Приклад.
Знайти значення
![]() за формулою (5).
за формулою (5).
Нехай
 .
Знаходимо послідовно при
.
Знаходимо послідовно при
 :
:
![]() ,
,
![]()
![]()
![]() .
.
Отже
![]() .
.
Для
відшукання
![]() можна скористатися методом Ньютона
розв’язування
рівняння
можна скористатися методом Ньютона
розв’язування
рівняння
![]() .
Дістаємо обчислювальну схему:
.
Дістаємо обчислювальну схему:
 .
(6)
.
(6)
Приклад.
Знайдемо
![]() .
.
За формулою (6) маємо
![]() .
.
Виконуємо рівняння:
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Отже,
![]() .
.
Аналогічно
можна знайти корені будь-якого степеня.
Зауважимо, що, як правило, корені не
можна точно виразити десятковим дробом.
Зазвичай корені є ірраціональними
числами, тобто їх не можна подати дробом
![]() ,
де
,
де
![]() — цілі числа.
— цілі числа.
![]()
Що називається степенем числа з натуральним показником?
Властивості степенів?
Що називається коренем
 -го
степеня з числа
-го
степеня з числа
 ?
?Що називається арифметичним коренем?
Властивості радикалів?
![]()
Спростити числовий вираз (1—5). Відповідь
 .
–3
.
–3 .
. 
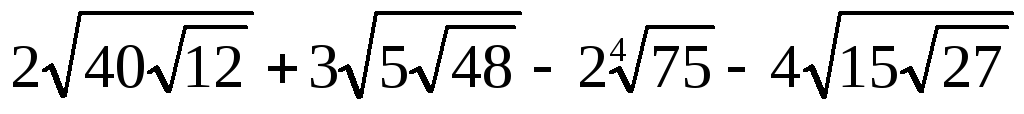 (0).
(0). .
. 
 .
.
![]() .
.
Перевірити правильність рівностей (6—15).
 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.
Спростити вирази і обчислити їх (16—27). Відповідь
16.
![]() .
.![]()
17.
![]() .
.![]()
18.
![]() .
.![]()
19.![]() .
.![]()
20.![]() . 3
. 3
21. ![]()
![]() .
.
22.
![]() .
. ![]()
23.
 .
. ![]()
24.
 .
. ![]()
25.
 .
. ![]()
26.
![]() . 3
. 3
27.
![]() .
. ![]()
Звільнитися від ірраціональності в знаменнику дробу (28—30).
