
1) Якщо , то ;
2) Якщо , то .
Приклад. Розв’язати нерівність
![]() .
.
-
Запишемо цю нерівність у вигляді (1):
![]()
звідки
знайдемо розв’язок
![]() або
або
![]()
Приклад. Розв’язати нерівність
![]() .
.
-
Запишемо нерівність у вигляді
![]() .
.
Звідси дістаємо:
![]() ,
,
![]() ,
,
![]() .
.
Найскладнішими є такі логарифмічні нерівності, в яких основи логарифмів залежать від х:
![]() (9)
(9)
Дістаємо дві системи нерівностей:
1)
![]() 2)
2)
![]() .
.
Об’єднання розв’язків цих систем і буде розв’язком нерівності (2).
Приклад. Розв’язати нерівність
![]()
-
Скориставшись співвідношенням
 розв’яжемо дві системи нерівностей:
розв’яжемо дві системи нерівностей:
1)
![]() 2)
2)
![]()
Шуканий
розв’язок:
![]()
Приклад. Розв’язати логарифмічну нерівність
![]()
-
Запишемо дану нерівність у вигляді (2):
![]()
Звідси дістаємо дві системи:
1)
![]() 2)
2)
![]()
Побудуємо
графік функції
![]() .
.
При
![]() маємо:
маємо:
![]() ,
,
![]()
При
![]() маємо:
маємо:
![]()
![]() ,
,
![]()
При
![]() маємо:
маємо:
![]()
![]()
![]()
Розв’язок
даної нерівності:
![]() .
.
9.8. Деякі типові задачі вищої математики, що зводяться до розв’язування системи нерівностей
Приклад. Знайти область існування функції
![]() .
.
-
Функція
 існує, якщо виконується система
нерівностей:
існує, якщо виконується система
нерівностей:
![]()
Нерівність
вигляду
![]() розв’язують, будуючи графік функції
розв’язують, будуючи графік функції
![]()
Отже,
будуємо графіки функцій
![]() ,
,
![]() і знаходимо
область, де одночасно виконуються обидві
нерівності
(рис. 1). Коли йдеться про строгу нерівність,
то відповідну
межу позначаємо пунктиром. Шукану
область заштриховуємо.
і знаходимо
область, де одночасно виконуються обидві
нерівності
(рис. 1). Коли йдеться про строгу нерівність,
то відповідну
межу позначаємо пунктиром. Шукану
область заштриховуємо.

Рис. 1.
Приклад. Знайти область існування функції
![]() .
.
-
Функція існує, якщо виконується нерівність

![]()
Шукану область зображено на рис. 2.

Рис. 2.
9.9. Тригонометричні нерівності
Розв’язування будь-якої тригонометричної нерівності зводиться до розв’язування однієї з наведених далі шести нерівностей.
1.
![]()

Рис. 1.
Із рис. 1 знаходимо розв’язок даної нерівності:
![]() . (1)
. (1)
Приклад. Розв’язати нерівність
![]()
-
Позначивши
 дістанемо квадратну нерівність:
дістанемо квадратну нерівність:
![]()
![]()
Повертаючись до початкових позначень, маємо:
![]() ;
;
![]()
2.
![]()
Із рис. 1 знаходимо розв’язок:
![]() . (2)
. (2)
Приклад. Розв’язати нерівність
![]()
-
Позначивши
 ,
дістанемо квадратну нерівність:
,
дістанемо квадратну нерівність:
![]()
Повернувшись до початкових позначень, розв’яжемо нерівності:
1)
![]() ;
;
2)
![]()
3.
![]()
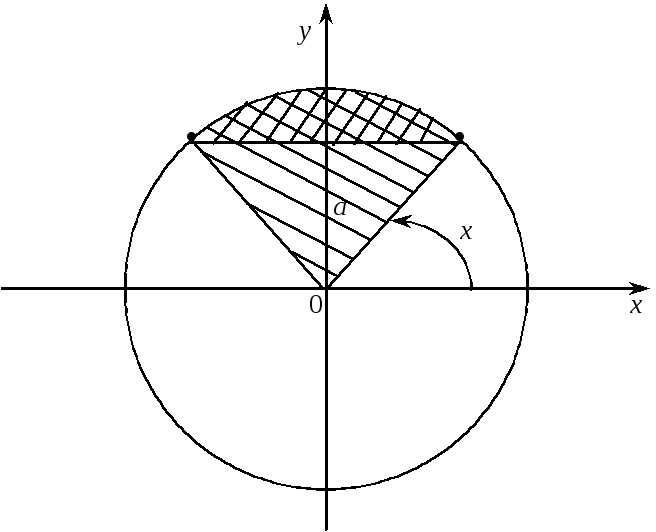
Рис. 2.
Із рис. 2 знаходимо розв’язок даної нерівності:
![]() (3)
(3)
Приклад. Розв’язати нерівність
![]()
-
Позначивши
 розв’яжемо нерівність
розв’яжемо нерівність
![]()
Переходячи до початкових позначень, маємо:
1)
![]()
2)
![]()
4.
![]()
Із рис. 2 знаходимо розв’язок даної нерівності:
![]() (4)
(4)
Приклад. Розв’язати нерівність
![]()
-
Позначивши
 розв’яжемо нерівність
розв’яжемо нерівність
![]()
Повертаюсь до початкових позначень, маємо:
1)
![]()
2)
![]()
![]()
![]()
5.
![]()

Рис. 3.
Із рис. 3 знаходимо розв’язок даної нерівності:
![]() (5)
(5)
Аналогічно
розв’язується нерівність
![]() :
:
![]() . (6)
. (6)
Приклад. Розв’язати нерівність
![]()
Виконавши
заміну![]() дістанемо
дістанемо
![]()
Повертаючись до початкових позначень, маємо:
![]()
![]()
6.
![]()

Рис. 4.
Із рис. 4 знаходимо розв’язок даної нерівності
![]() (7)
(7)
Аналогічно
розв’язується нерівність
![]() :
:
![]() . (8)
. (8)
Приклад. Розв’язати нерівність
![]()
-
Позначивши
 дістаємо
дістаємо

Повертаючись до початкових позначень, маємо:
![]()
![]()
Приклад. Розв’язати нерівність
![]()
-
Позначивши
 дістаємо нерівність:
дістаємо нерівність:
![]()
Повертаючись до початкових позначень, маємо:
1)
![]()
2)
![]()
9.10. Алгебраїчні нерівності
Наведемо деякі відомі нерівності, часто використовувані під час розв’язування різних задач.
1. Нерівність Коші:
 (1)
(1)
2. Нерівність Гельдера
 (2)
(2)
якщо
![]() ;
;
![]()
3.
![]() якщо
якщо
![]() (3)
(3)
Приклад. Довести нерівність
![]()
-
Якщо
 ,
то нерівність, очевидно, виконується.
,
то нерівність, очевидно, виконується.
Якщо
![]() ,
підносимо обидві частини нерівності
до квадрата:
,
підносимо обидві частини нерівності
до квадрата:
![]()
![]() .
Нерівність доведено.
.
Нерівність доведено.
Приклад.
Довести, що для будь-якого трикутника
зі сторонами
![]() виконується нерівність
виконується нерівність
![]()
-
Оскільки обидві частини нерівності додатні, то підносимо їх до квадрата:
![]()
![]()
Оскільки
![]() то
нерівність
доведено.
то
нерівність
доведено.
Приклад. Довести нерівність
![]() .
.
-
Помноживши обидві частини нерівності на 2, дістанемо:
![]() звідки
звідки
![]()
![]()
Остання нерівність, очевидно, виконується, що й доводить дану нерівність.
Приклад. Довести, що при будь-яких додатних значеннях а і b виконується нерівність
![]()
-
Підносимо обидві частини нерівності до квадрата:
![]()
![]()
![]()
У результаті тотожних перетворень дістали правильну нерівність, що й доводить дану нерівність.
Приклад.
Довести, що
![]() коли
коли
![]()
-
Узявши
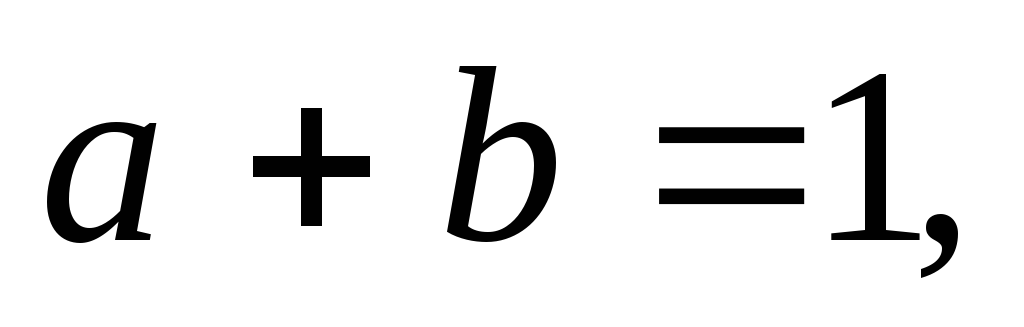 розглянемо функцію
розглянемо функцію

 Щоб відшукати мінімум функції
Щоб відшукати мінімум функції
 ,
знайдемо її похідну:
,
знайдемо її похідну:
![]() .
.
З
рівняння
![]() випливає:
випливає:
![]()
Отже,
![]() ,
,
![]() ,
,
![]() .
.
Якщо
![]() ,
то
,
то
![]()
Приклад. Довести нерівність
![]() .
.
-
Розкриваючи дужки, дістаємо:
![]()
![]()
![]()
У результаті тотожних перетворень дістаємо нерівність, яка, очевидно, виконується, що й доводить дану нерівність.
![]()
1. Сформулюйте властивості нерівностей.
2. Як розв’язуються квадратні нерівності?
3. У чому полягає метод інтервалів?
4. Як розв’язуються ірраціональні нерівності?
5. Розв’язування показникових нерівностей.
6. Розв’язування логарифмічних нерівностей.
7. Розв’язування тригонометричних нерівностей.
![]()
Розв’язати нерівність (1—49).
