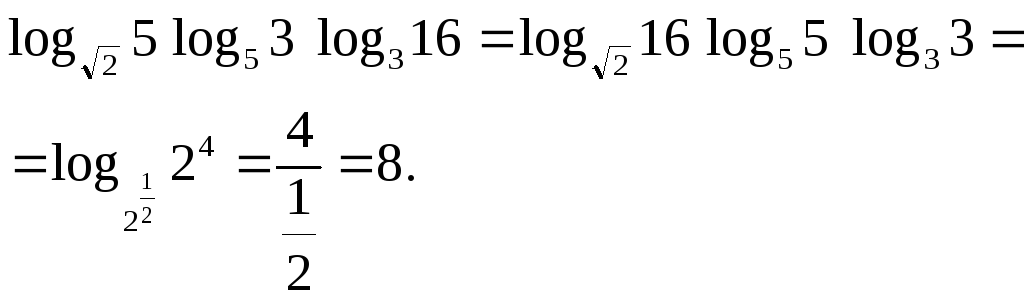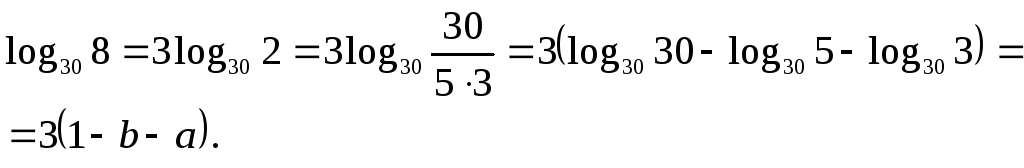учебное пособие / лекція 8
.docЛЕКЦІЯ
ПОКАЗНИКОВІ ТА ЛОГАРИФМІЧНІ РІВНЯННЯ
Відомості із вищої математики. Для наближеного обчислення показникової і логарифмічної функцій можна використати такі розклади
![]() ,
,
![]()
Збіжність послідовності також маємо, якщо
![]()
![]()
Показникову функцію можна розкласти в ряд:
![]()
Збіжність ряду можна поліпшити, узявши
![]()
Значення логарифмів можна знайти з таких розкладів:
![]()
![]()
![]()
![]()
Узявши
![]() ,
дістанемо такий розклад:
,
дістанемо такий розклад:
![]()
Ці розклади можна використовувати в разі комплексних значень аргументів. В подальшому припускаємо, що всі аргументи і функції є дійсними.
8.1. Показникова функція
Наведемо
деякі основні властивості показникової
функції
![]()
1.
![]() . 5.
. 5.
![]() .
.
2.
![]() . 6.
. 6.
![]() .
.
3.
![]() . 7.
. 7.
![]() .
.
4.
![]() .
.
Якщо
![]() ,
показникова функція
,
показникова функція
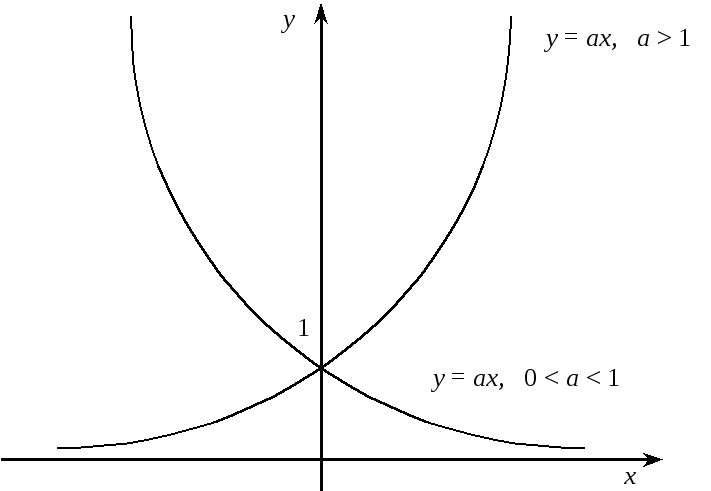
![]() зростає при всіх значеннях х;
якщо
зростає при всіх значеннях х;
якщо
![]() ,
ця функція спадає при всіх значеннях х
(див. рисунок).
,
ця функція спадає при всіх значеннях х
(див. рисунок).
8.2. Логарифмічна функція
Логарифмічна
функція
![]() — це функція, обернена до показникової
функції
— це функція, обернена до показникової
функції
![]()
Якщо
![]() ,
логарифмічна функція зростає при
,
логарифмічна функція зростає при
![]() ;
якщо
;
якщо
![]() ,
логарифмічна функція спадає при
,
логарифмічна функція спадає при
![]() (див. рисунок).
(див. рисунок).
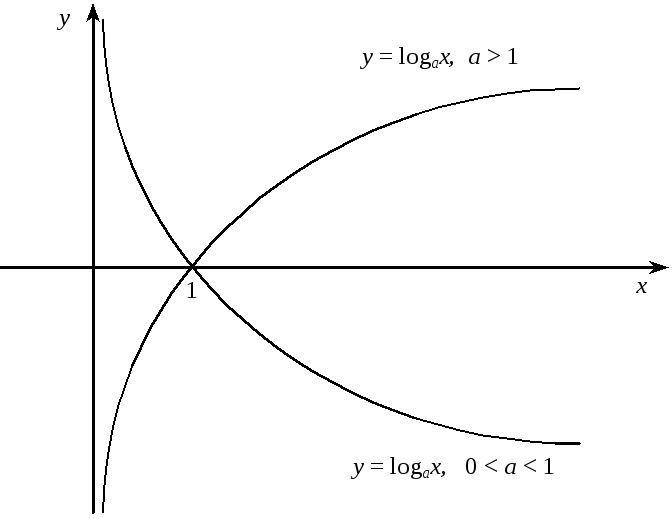
Логарифмом числа b при основі а називається степінь, до якого потрібно піднести основу а, щоб дістати число b:
![]()
Звичайно
вважають, що
![]()
Основна логарифмічна тотожність:
![]()
Наведемо деякі властивості логарифмів.
1.
![]() .
.
2.
![]() .
.
3.
![]() .
.
4.
![]() .
.
5.
![]() .
.
6.
![]() .
.
7. Формула
переходу до нової основи
![]() :
:
![]() .
.
8.
![]() .
.
9.
![]() .
.
10.
![]()
11.
![]() .
.
12.
![]() .
.
Доведення формул (8—11) випливає з формули (7).
8.3. Приклади перетворень логарифмічних виразів
Обчислити значення виразів (1—12).
1.
![]()
-
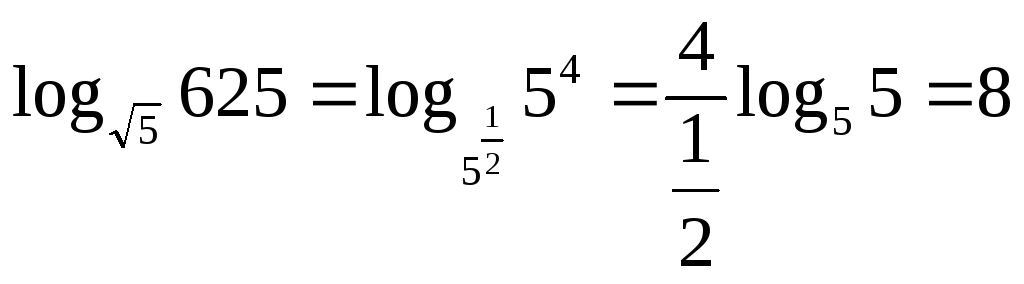 .
.
2.
![]()
-
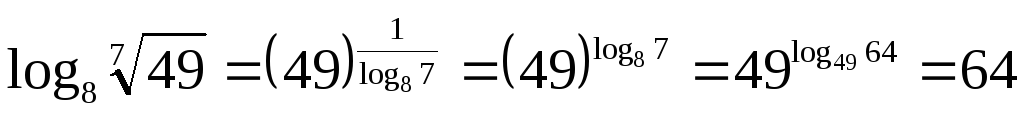 .
.
3.
![]()
-
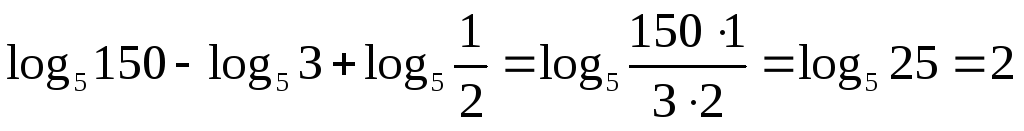 .
.
4.
![]() .
.
5.
![]()
-
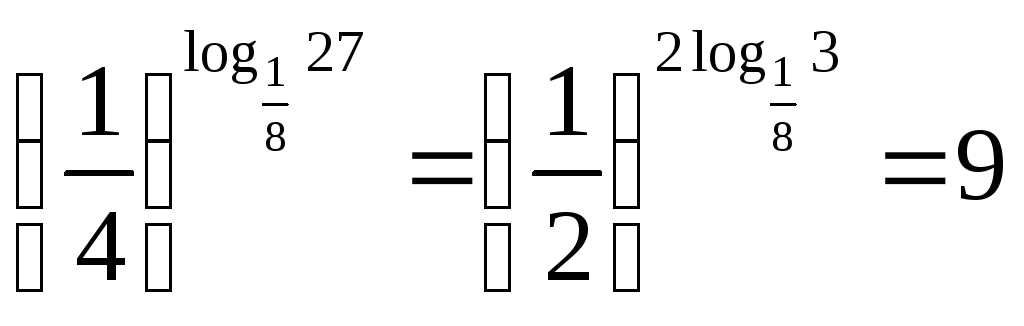 .
.
6.
![]() .
.
-
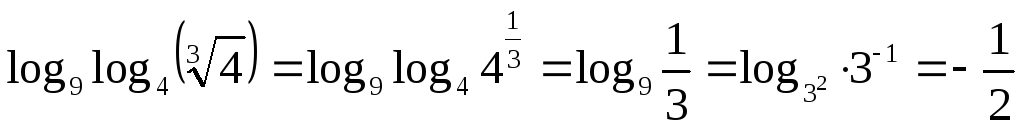 .
.
7.
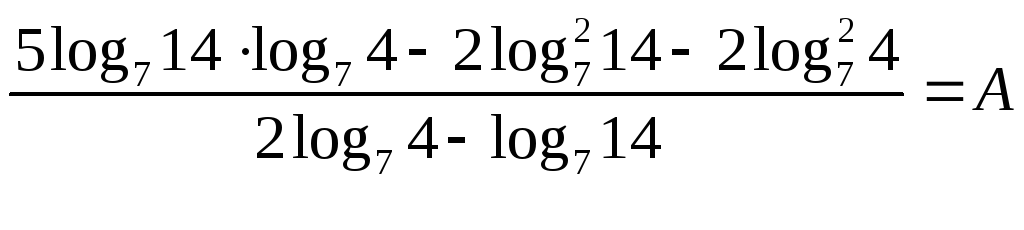 .
.
-
Позначимо
 ,
тоді
,
тоді
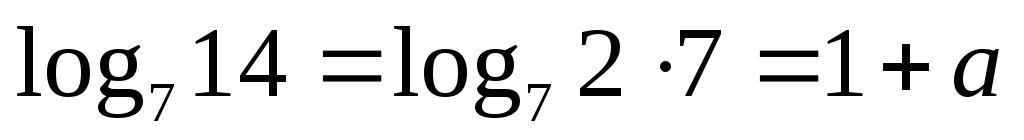 ,
,
![]() .
.
Остаточно маємо:
![]()
8.
![]()
-
Позначивши
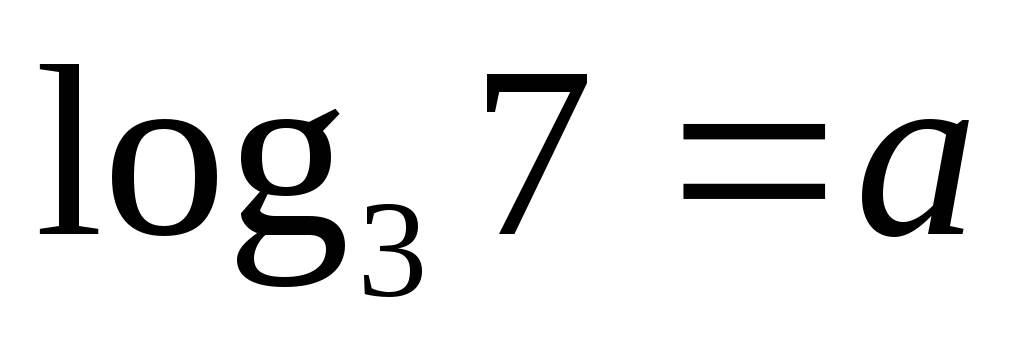 ,
дістанемо:
,
дістанемо:
![]() .
.
Остаточно маємо:
![]() .
.
9.
![]()
-
 .
.
10.
![]()
-
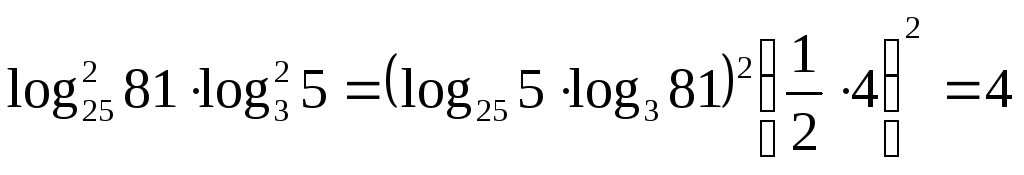 .
.
11.
![]()
12.
![]()
13.
Знайти
![]() ,
якщо
,
якщо
![]() .
.
-
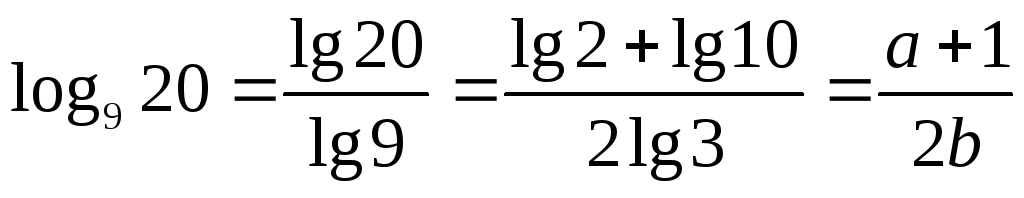 .
.
14.
Дано:
![]() .
Знайти
.
Знайти
![]() .
.
15.
Знайти
![]() ,
якщо
,
якщо
![]() .
.
-
Переходимо до основи х:
![]() ;
;
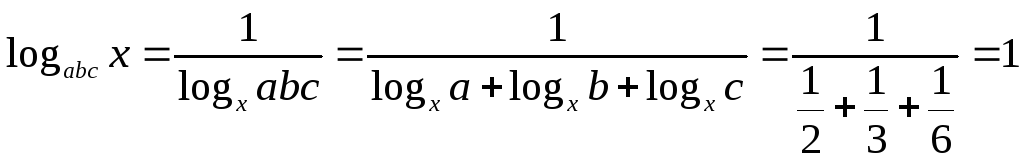 .
.
8.4. Способи розв’язання логарифмічних рівнянь
1. Перехід до спільної основи. Якщо в рівнянні маємо логарифми з різними основами, то переходимо до спільної основи.
Приклад.
Розв’язати рівняння
![]() .
.
-
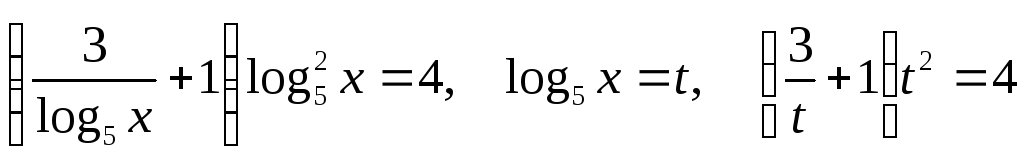 ,
,
![]()
Приклад.
Розв’язати рівняння
![]() .
.
-
Переходимо до основи 5:
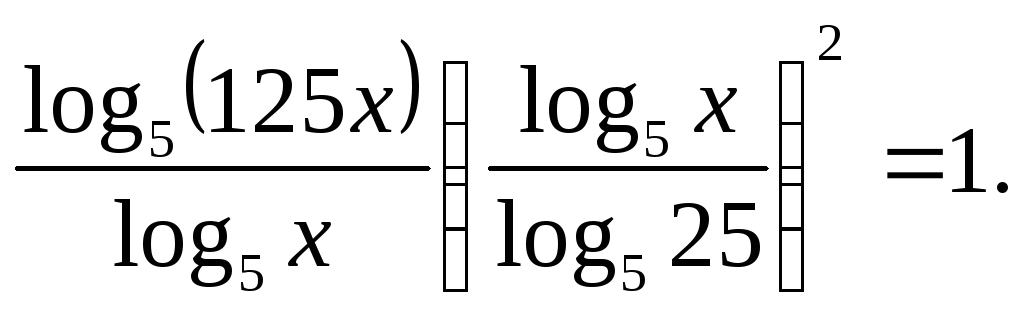 Позначивши
Позначивши
 дістанемо
дістанемо
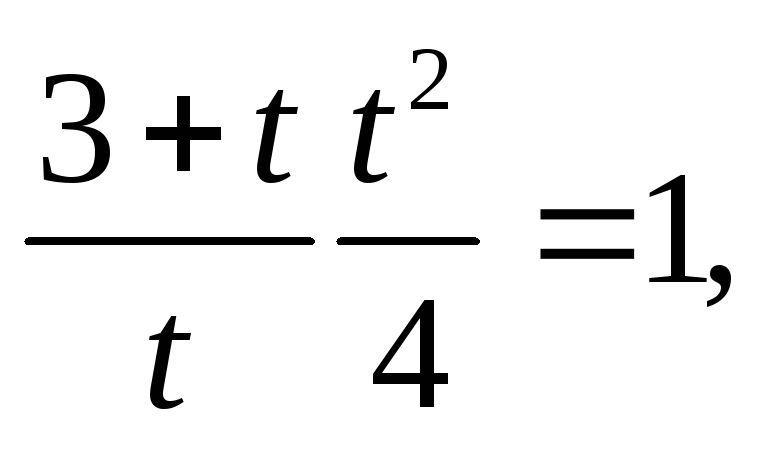 звідки
звідки
![]() .
.
2. Потенціювання. Якщо під знак логарифма входить сума або різниця, то рівняння потенціюють. Розв’язок неодмінно перевіряють.
Приклад.
![]() .
.
-
Перейдемо до основи 2:
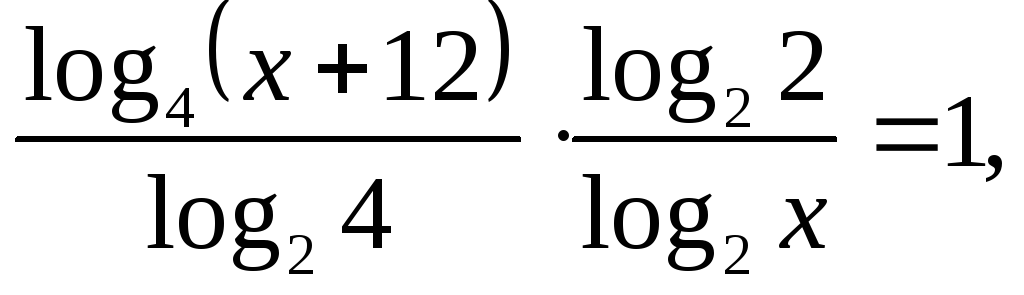
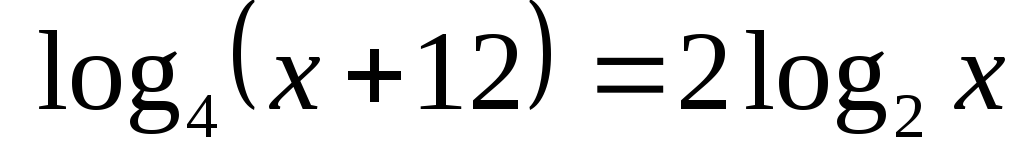 .
.
Далі
виконуємо потенціювання:
![]() .
.
Корінь
![]() не задовольняє рівняння.
не задовольняє рівняння.
Приклад.
Розв’язати рівняння
![]()
-
За умовою маємо:
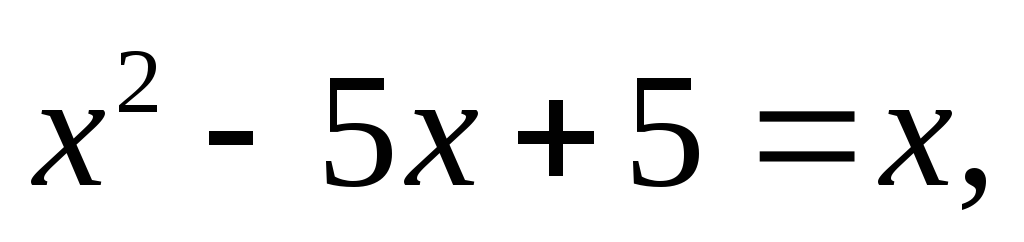 звідки
звідки
 .
.
Корінь
![]() не задовольняє рівняння.
не задовольняє рівняння.
3. Логарифмування. Якщо в показник при невідомому входять логарифми невідомого, то звичайно обидві частини рівняння логарифмують.
Приклад.
Розв’язати рівняння
![]()
-
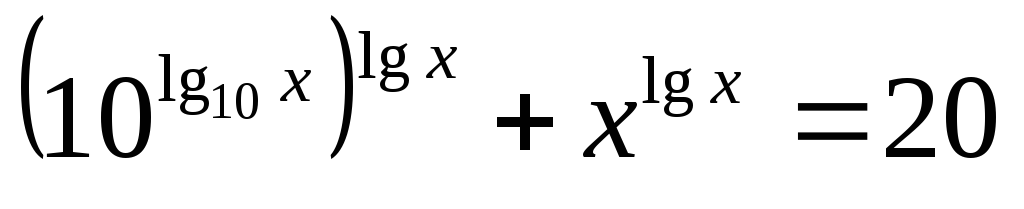 ,
,
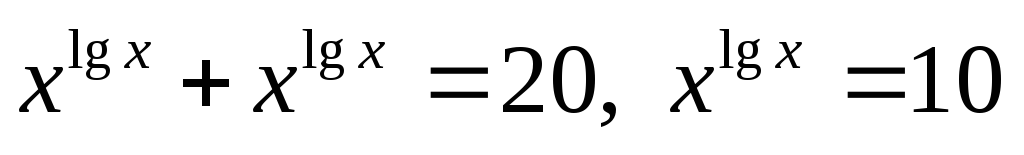 .
.
Логарифмуємо
обидві частини рівняння за основою 10:
![]() .
.
4. Метод заміни змінної. Логарифмічне рівняння зводиться до алгебраїчного рівняння.
Приклад.
Розв’язати рівняння
![]() .
.
Позначимо
![]()
![]()
![]()
![]()
Приклад.
Розв’язати рівняння
![]()
-
Позначимо
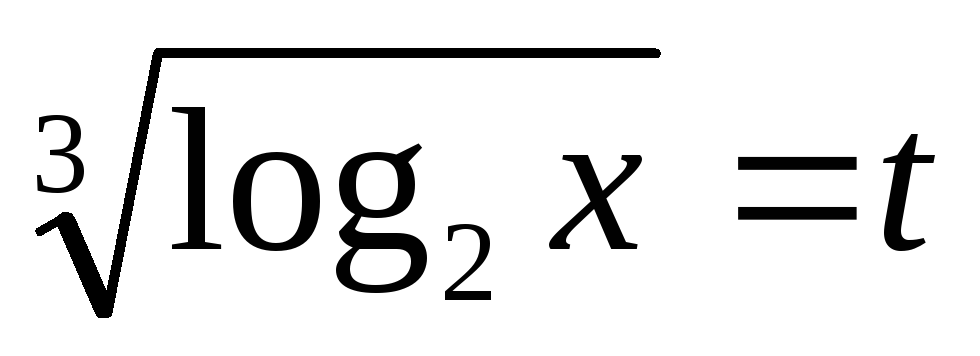 .
Тоді
.
Тоді
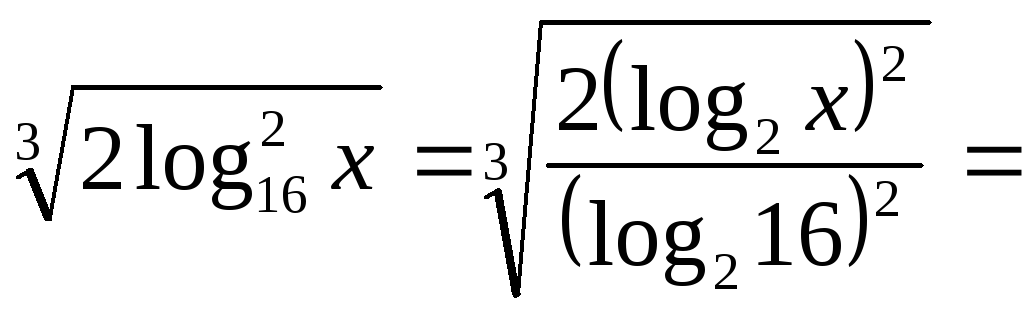


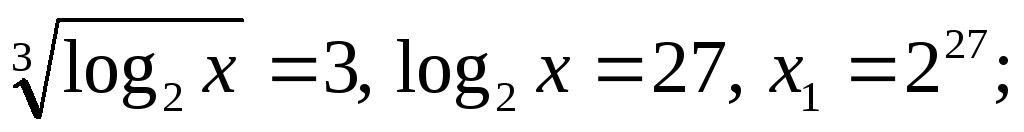
![]()
5.
Розклад на множники. Рівняння
подається у вигляді
![]() і кожний множник прирівнюється до нуля.
і кожний множник прирівнюється до нуля.
Приклад. Розв’язати рівняння
![]()
Далі
маємо:
![]()
Приклад. Розв’язати рівняння
![]() .
.
-
Позначивши
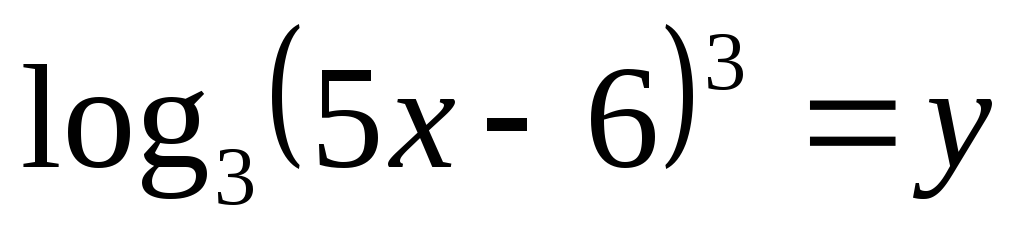 ,
,
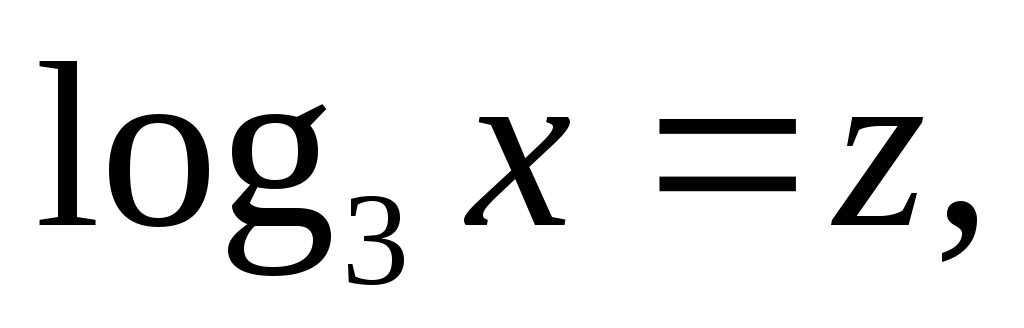 дістанемо рівняння
дістанемо рівняння
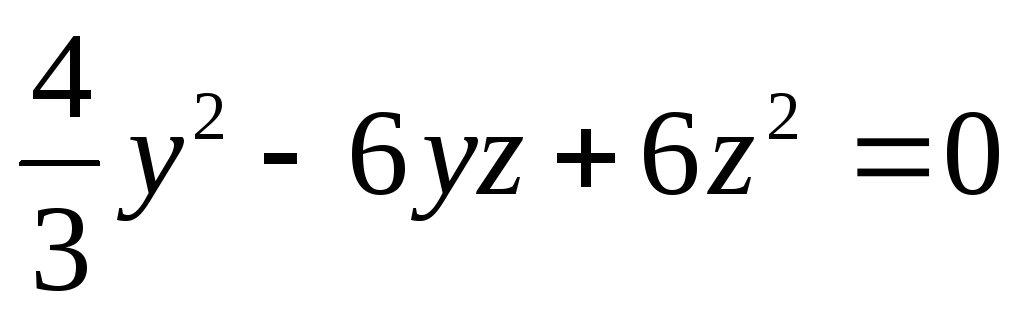 ,
або
,
або
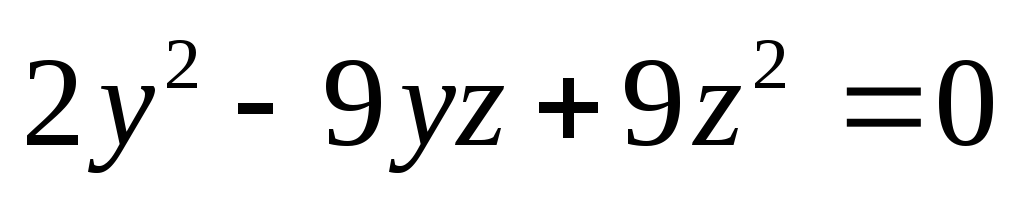 ,
звідки маємо
,
звідки маємо
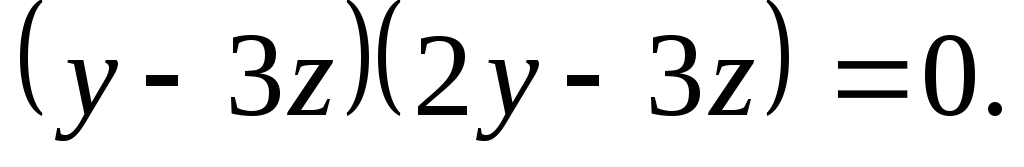 Прирівнюємо до нуля кожний множник:
Прирівнюємо до нуля кожний множник:
1)
![]()
2)
![]()
Корінь
![]() не задовольняє рівняння.
не задовольняє рівняння.
6.
Графічний спосіб розв’язування.
Рівняння записують у вигляді
![]() .
Далі будують графіки функцій
.
Далі будують графіки функцій
![]()
![]() і відшукують точки їх перетину, які
визначають розв’язок рівняння.
і відшукують точки їх перетину, які
визначають розв’язок рівняння.
Приклад.
Розв’язати графічно рівняння
![]() .
.
-
Графіки функцій
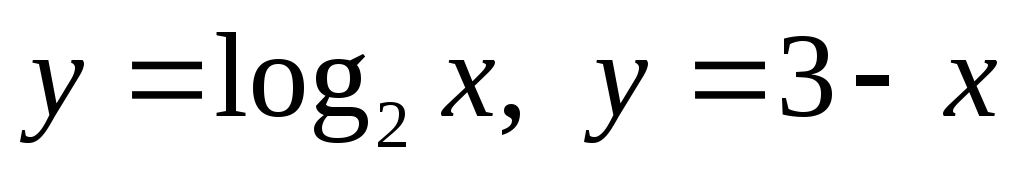 перетинаються в точці
перетинаються в точці
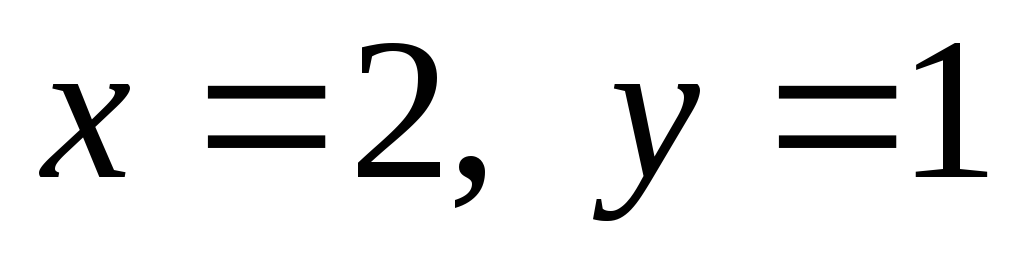 .
Маємо розв’язок
.
Маємо розв’язок
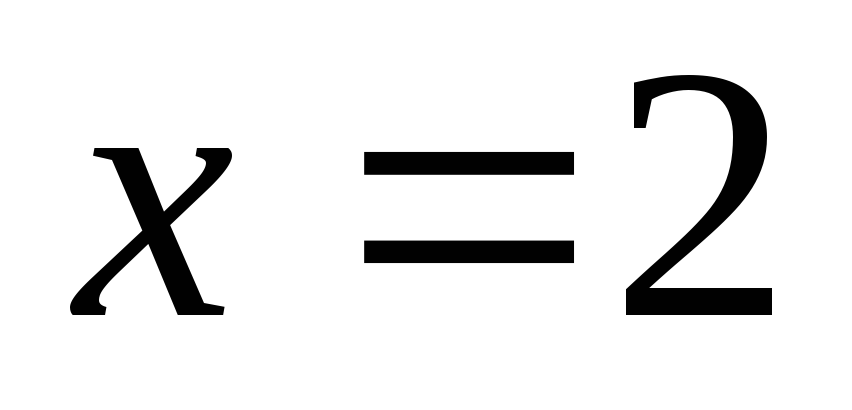 .
.
Розв’язуючи логарифмічні рівняння здебільшого застосовують кілька способів їх перетворення.
Приклад.
Розв’язати рівняння
![]() .
.
-
Переходимо до основи 3:
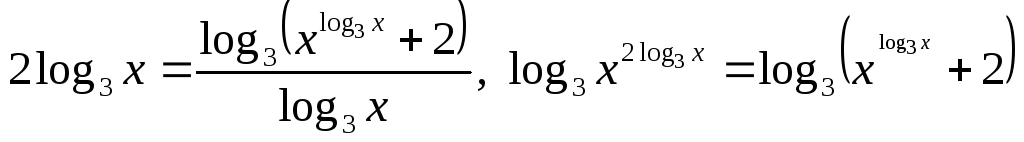 .
.
Потенціюємо рівняння:
![]() ;
;
![]() ;
;
![]() .
.
Логарифмуємо рівняння за основою 3:
![]()
Приклад. Розв’язати рівняння
![]() .
.
-
Розглядаємо два випадки:
1)
![]() ,
тоді рівняння перетворюється на
тотожність
,
тоді рівняння перетворюється на
тотожність
![]() звідки
звідки
![]() ;
;
2)
![]() ,
тоді
,
тоді
![]() .
.
Потенціюємо рівняння:
![]()
8.5. Способи розв’язування показникових рівнянь
1. Прирівнювання показників при однаковій основі
Із
рівності
![]() випливає
випливає
![]() .
.
Приклад.
Розв’язати рівняння
![]() .
.
-
Записавши рівняння у вигляді
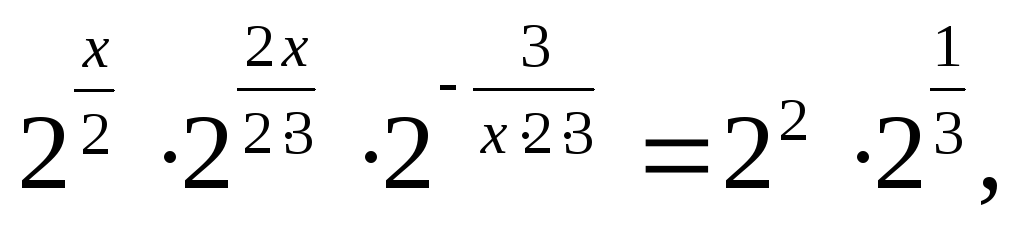 прирівняємо
показники при основі 2:
прирівняємо
показники при основі 2:
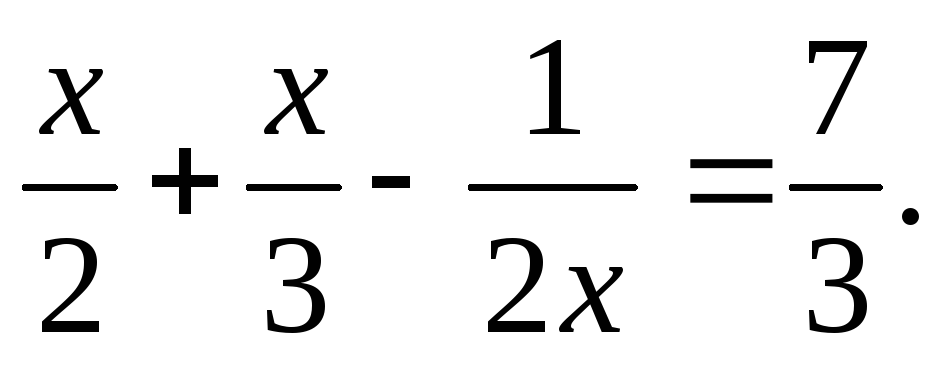
Далі
маємо:
![]() .
.
Приклад.
Розв’язати рівняння
![]() .
.
-
Прирівнюємо показники при основі 5:
![]() ,
або
,
або
![]() Позначивши
Позначивши
![]() дістанемо:
дістанемо:
![]() .
.
Корінь
![]() не задовольняє рівняння.
не задовольняє рівняння.
2. Логарифмування рівняння
Приклад.
Розв’язати рівняння
![]() .
.
-
Логарифмуємо обидві частини рівняння при основі 3:
![]() ,
,
![]() .
.
Приклад.
Розв’язати рівняння
![]() .
.
-
Оскільки
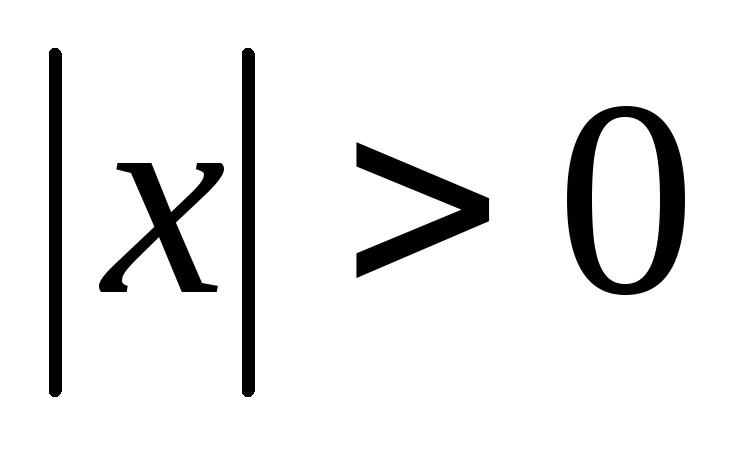 ,
то можна логарифмувати рівняння.
,
то можна логарифмувати рівняння.
![]() .
.
3. Метод заміни змінної
Приклад.
Розв’язати рівняння
![]()
-
Позначивши
 ,
дістанемо:
,
дістанемо:
![]() ;
;
![]() .
.
Приклад.
Розв’язати рівняння
![]()
-
Позначивши
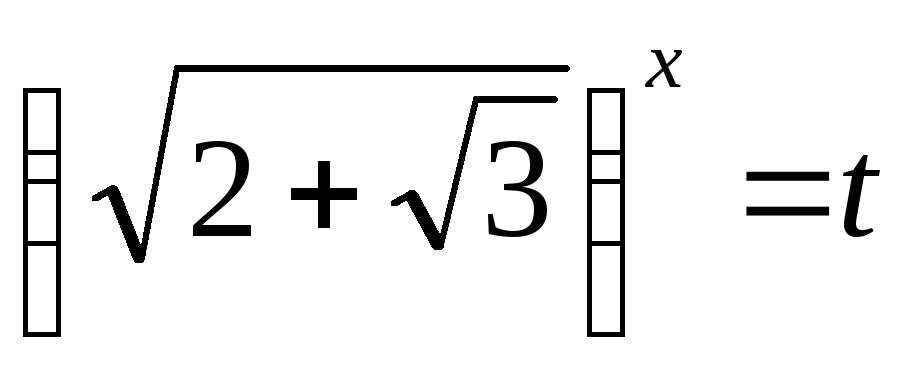 ,
дістанемо
,
дістанемо
 ;
;
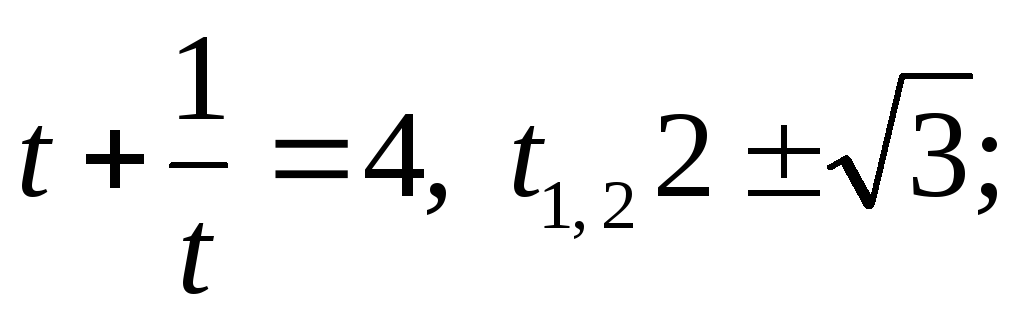
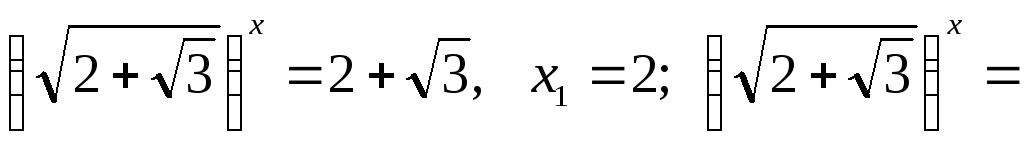
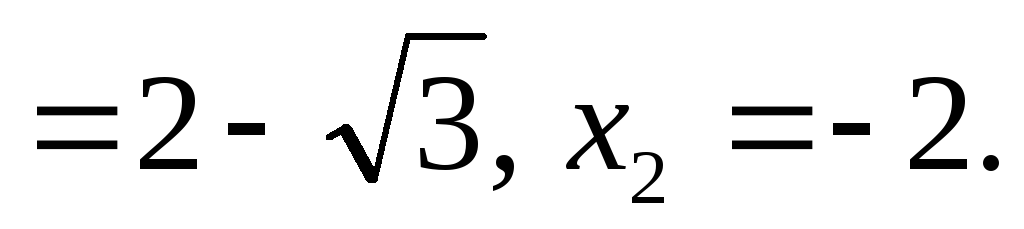
Приклад.
Розв’язати рівняння
![]() .
.
-
Позначивши
 дістанемо:
дістанемо:

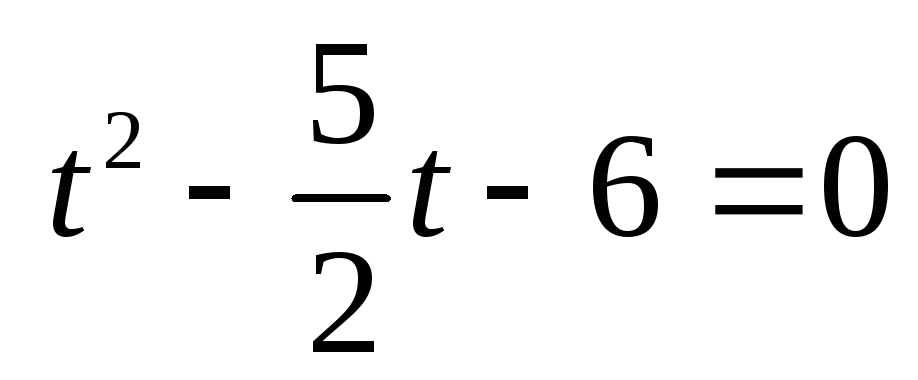 ;
;
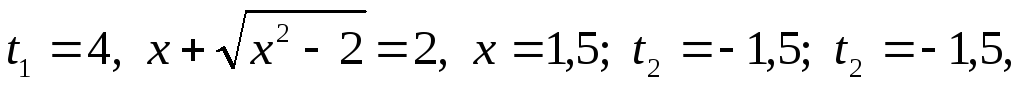
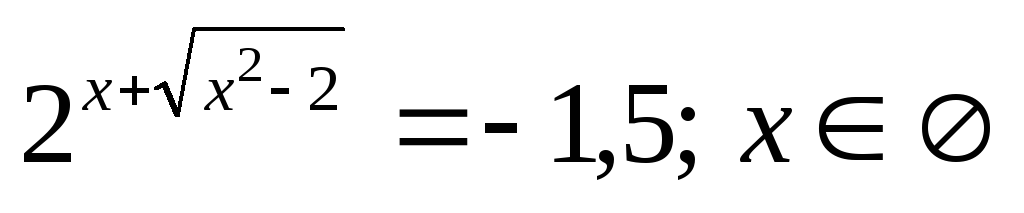 .
.
4. Однорідні рівняння
Рівняння
![]() можна переписати у вигляді
можна переписати у вигляді
![]() .
.
Виконавши
заміну,
![]() ,
дістанемо рівняння
,
дістанемо рівняння
![]() .
.
Приклад.
Розв’язати рівняння
![]() .
.
-
Перепишемо рівняння у вигляді:
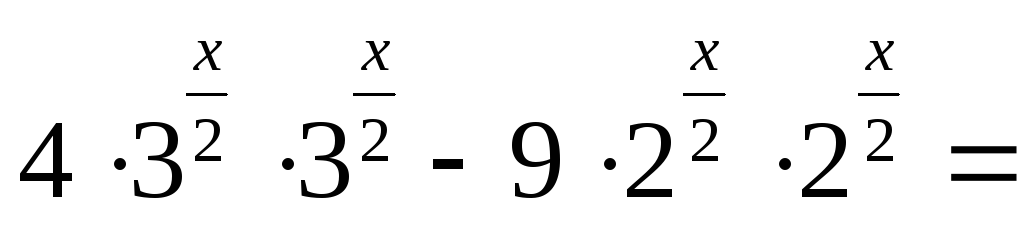
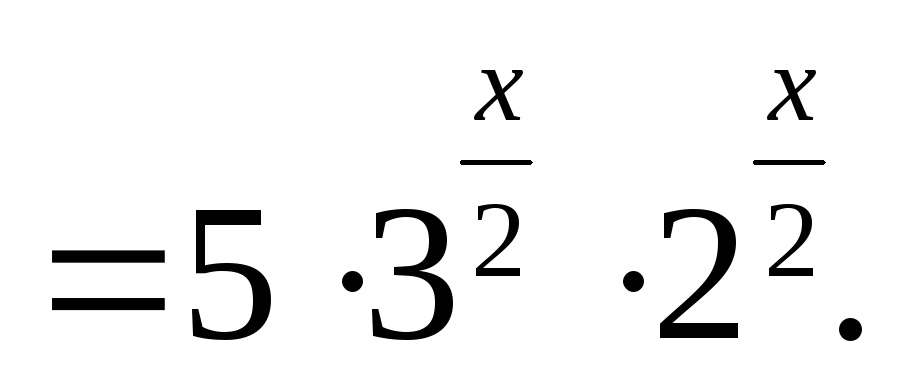 Виконавши заміну
Виконавши заміну
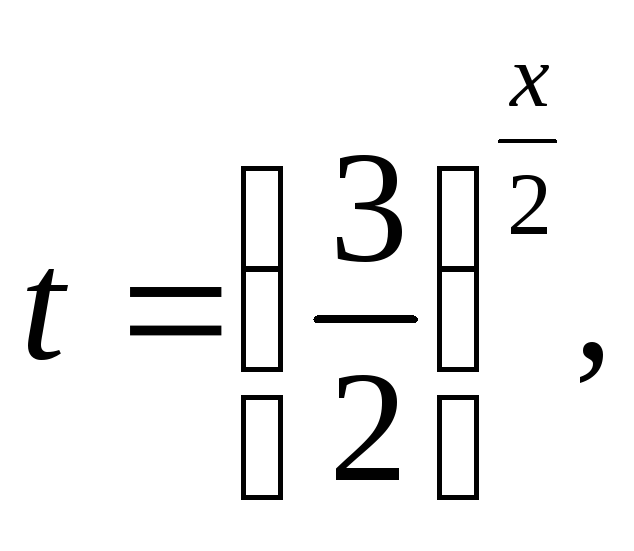 дістанемо
дістанемо
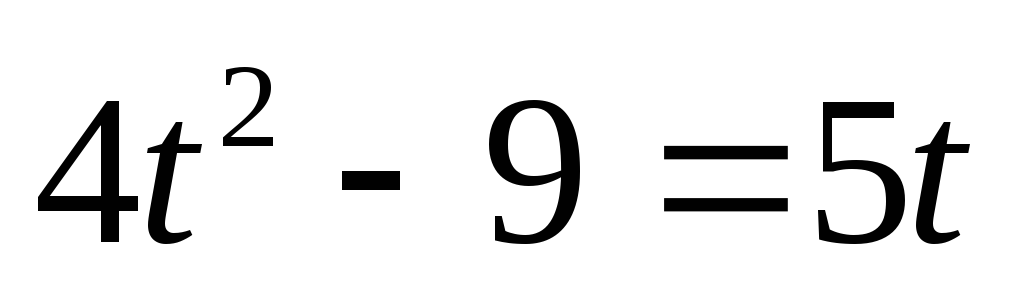 ,
звідки
,
звідки
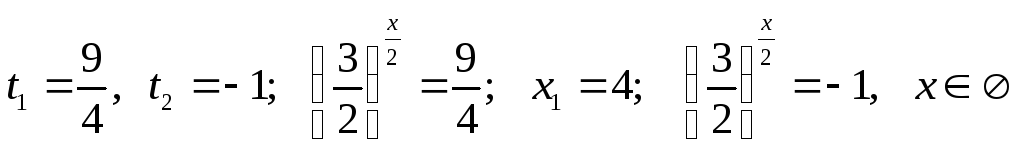 .
.
Приклад.
Розв’язати рівняння
![]()

х ≈ 1,18681439.
Приклад.
Розв’язати рівняння
![]()
-
Запишемо рівняння у вигляді:
![]()
Позначивши
![]() ,
дістанемо:
,
дістанемо:
![]() .
.
5. Розклад рівняння на множники
Рівняння
![]() намагаємося подати у вигляді
намагаємося подати у вигляді
![]() і прирівнюємо до нуля кожний множник.
і прирівнюємо до нуля кожний множник.
Приклад.
Розв’язати рівняння
![]() .
.
-
Узявши
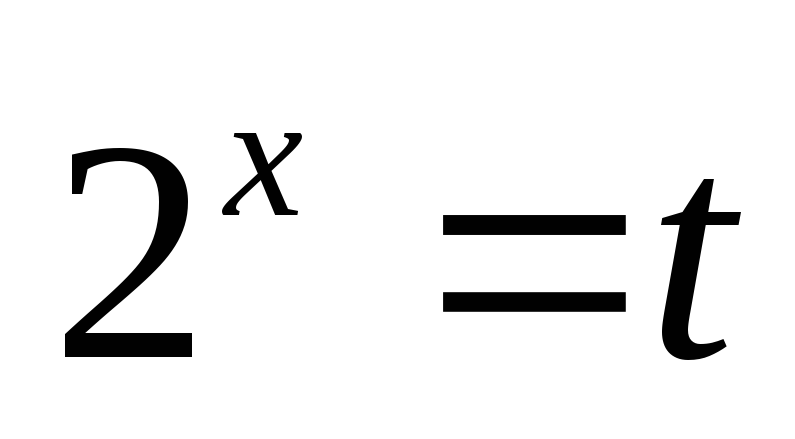 ,
розкладемо рівняння
,
розкладемо рівняння

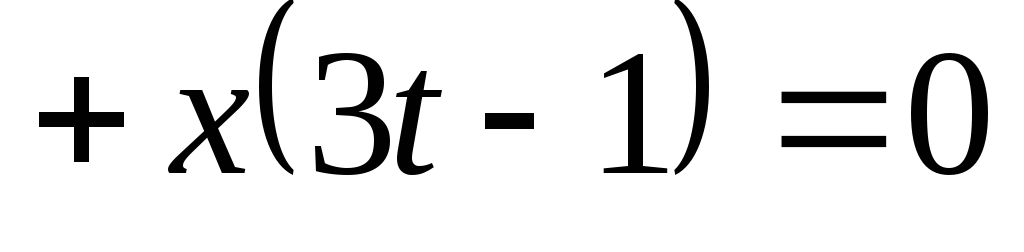 на
множники:
на
множники:
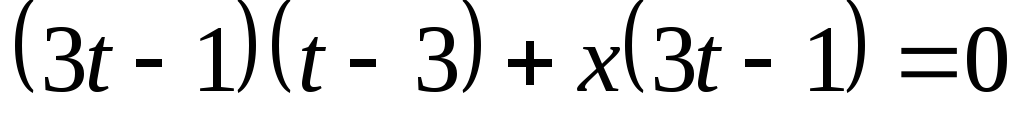 .
Далі маємо:
.
Далі маємо:
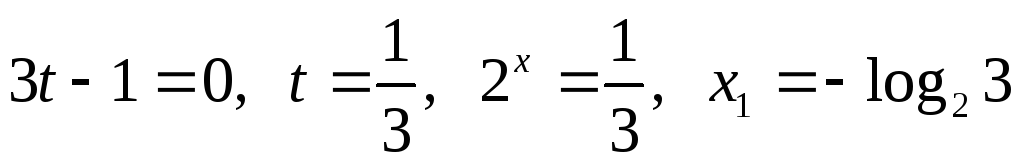 ;
;
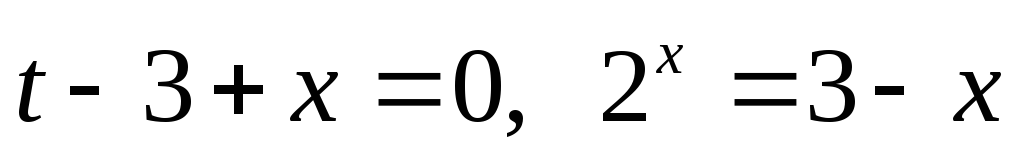 .
Розв’язавши
останнє рівняння графічно, знаходимо
корінь
.
Розв’язавши
останнє рівняння графічно, знаходимо
корінь
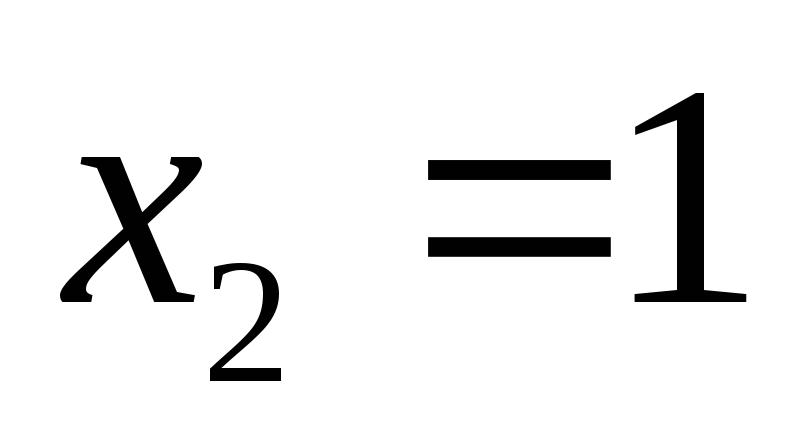 .
.
Приклад. Розв’язати рівняння
![]() .
.
-
Узявши
 ,
згрупуємо члени з множниками
,
згрупуємо члени з множниками
 :
:
![]() .
.
Прирівняємо кожний множник до нуля:
1)
![]() 2)
2)
![]() ,
,
![]() ;
;
![]() .
Корінь
.
Корінь
![]() не задовольняє рівняння.
не задовольняє рівняння.
8.6. Показниково-степеневі рівняння
Розглядається рівняння
![]() .
.
Наведемо частинні випадки цього рівняння.
1)
![]() ,
функція
,
функція
![]() існує.
існує.
2)
![]() ,
функції
,
функції
![]() існують.
існують.
3)
![]() ,
,
![]() ,
,
![]() .
.
4)
![]() ,
а
,
а
![]() — цілі числа одинакової парності.
— цілі числа одинакової парності.
Приклад.
Розв’язати рівняння
![]() .
.
-
1.
 .
.
2.
![]() .
.
3.
![]() .
Підставляючи
.
Підставляючи
![]() в рівняння, дістаємо
в рівняння, дістаємо
![]() .
Оскільки вираз
.
Оскільки вираз
![]() не має сенсу, то корінь
не має сенсу, то корінь
![]() не задовольняє рівняння.
не задовольняє рівняння.
4.
![]() .
.
Приклад.
Розв’язати рівняння
![]() .
.
-
1.
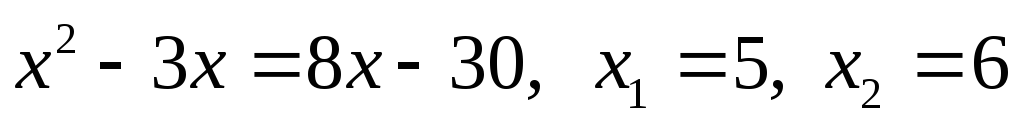 .
.
2.
![]() .
.
3.
![]() — не задовольняє рівняння.
— не задовольняє рівняння.
4.
![]() .
.
Деякі рівняння можна розглядати і як показникові, і як логарифмічні.
Приклад.
Розв’язати рівняння
![]() .
.
-
Потенціюємо обидві частини рівняння:
![]() Позначивши
Позначивши
![]() ,
дістанемо:
,
дістанемо:
![]() .
.
Приклад.
Розв’язати рівняння
![]() .
.
-
Переходимо до основи 3:
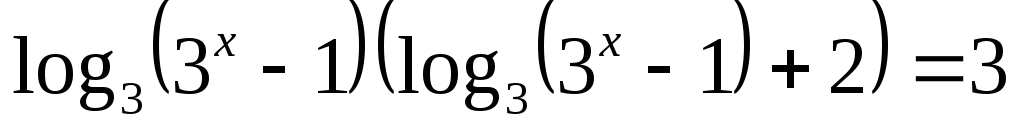 .
.
Позначивши
![]() дістанемо
дістанемо
![]() звідки
звідки
![]()
![]()
Повертаючись до початкових позначень, маємо:
1)
![]()
2)
![]() .
.
Приклад.
Розв’язати рівняння
![]() .
.
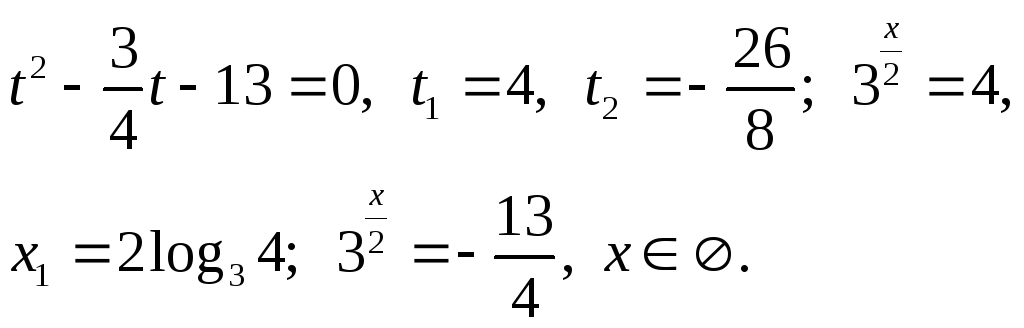
8.7. Системи показникових і логарифмічних рівнянь
Під час розв’язування систем показникових і логарифмічних рівнянь поєднують прийоми, застосовувані під час розв’язування відповідних рівнянь і систем алгебраїчних рівнянь.