Chast_4_4_l_30_31

316

Предположим, что после снятия внешнего магнитного поля известно распределение вектора намагниченности J P внутри постоянного магнита.

Уравнения поля внутри магнита:

уравнениях, получим разные способы расчета поля. Исключим в уравнениях

B и оставим только H . Для этого воспользуемся материальным уравнением

(третьим уравнением системы (4.137)) rot H 0,

div H div J .

В предыдущей лекции мы получали такую систему уравнений. Было обозначено div J м (4.128). Тогда система уравнений приобретает вид

(4.129), (4.130).

В предыдущей лекции также было показано, что кроме магнитных зарядов в объеме ферромагнетика с плотностью м div J , возникают магнитные заряды на поверхности магнита с поверхностной плотностью

м Jn , где n - нормаль к поверхности магнита, направленная во внешность.

На границе двух постоянных магнитов (рис. 4.63) с разными нормальными компонентами вектора намагниченности также возникает магнитный заряд с поверхностной плотностью

м J1n J2n ,

Рис. 4.63. Граница двух постоянных магнитов

317

где нормаль n направлена из первого ферромагнетика во второй. Это

где

м P divJ P ; м P Jn P .

Теперь из системы уравнений (4.137) исключим поле H , т.е. оставим только поле B . Для этого выразим H из третьего уравнения и подставим в первое. Тогда получим

Следует заметить, что микро является не фиктивной плотностью тока,

в отличие от магнитных зарядов, а реально существующей плотностью тока.

Кроме микротоков в объеме магнита существуют еще микротоки на поверхности магнита или на границе раздела магнитов. Для того чтобы это

318

где S1 - поверхность, натянутая на замкнутый контур l1 , dl и dS связаны правилом правоходового винта.

Рассмотрим участок поверхности S магнита (рис. 4.64). Возьмем точку на поверхности S . Проведем из этой точки три взаимно перпендикулярных единичных вектора: внешнюю нормаль n , касательный вектор и

касательный вектор , причем , n , составляют правую тройку векторов

(на рис. 4.64 вектор направлен «от нас»).

Рис. 4.64. К выводу выражения для поверхностной плотности микротока

Обозначим поверхностную плотность микротока через jмикро . Возьмем замкнутый контур l1 в виде прямоугольника, плоскость которого совпадает с плоскостью, образованной векторами и n . Запишем выражение (4.142) для

Такое выражение справедливо для любого касательного направления и соответствующего направления . Поэтому формулу (4.143) можно записать в векторном виде:

Из (4.144) легко следует (4.143).

Если граничат два магнита и нормаль выбрана из первого магнита во второй, то поверхностная плотность микротока на границе будет равна

где J1 - вектор намагниченности в точке границы первого магнита, J2 -

второго магнита.

319

Уравнения (4.141) совпадают с уравнениями магнитного поля стационарных токов в вакууме (2.128). По аналогии с этим магнитным полем и с учетом поверхностных микротоков, в соответствии с формулой Био-

Савара-Лапласа, магнитное поле B можно рассчитать по формуле:

Рассмотрим еще третий способ расчета магнитного поля постоянных магнитов при известном распределении вектора намагниченности.

Так как вектор намагниченности J - это магнитный момент единицы

объема магнетика, то магнитный момент элементарного объема dVP

магнетика будет J P dVP . Воспользовавшись формулой (2.160) для поля

системы токов с магнитным моментом для постоянного магнита получим:

Какую из формул (4.138), или (4.145), или (4.146) целесообразно использовать (или какую модель постоянного магнита целесообразно использовать), зависит от геометрии постоянного магнита и от характера распределения вектора намагниченности.

Так, например, если постоянный магнит имеет форму диска однородно намагниченного перпендикулярно основанию, причем толщина диска h

существенно меньше диаметра d (рис. 4.65), то для расчета магнитного поля целесообразно применить зарядовую модель.

Рис. 4.65. Постоянный магнит в виде диска, намагниченного перпендикулярно основанию

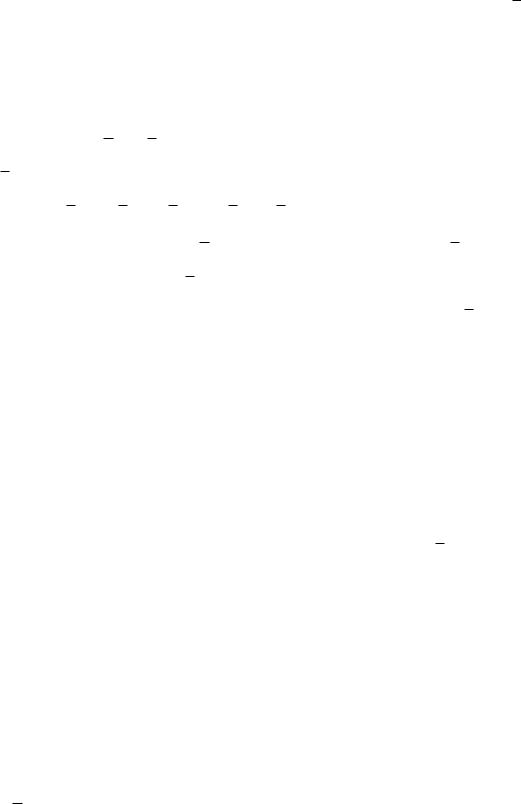
320

Поверхностная плотность магнитных зарядов на правом основании в этом случае будет равна м J , а на левом основании м J . Поле H

внутри магнетика может быть найдено по аналогии с электрическим полем плоского конденсатора.

H м J .

Или в векторной форме H J .

Поле B внутри магнита

B 0H 0J 0J 0J 0.

Вне магнита магнитное поле H существенно меньше поля H внутри магнита. Точное значение поля B (вне и внутри магнита) легче найти с использованием токовой модели. Для этого необходимо найти поле B витка

стоком iмикро J d .

Вкачестве второго примера рассмотрим постоянный магнит в виде весьма длинного кругового цилиндра, т.е. цилиндра, у которого длина l

существенно больше диаметра d . Магнит однородно намагничен вдоль оси цилиндра (рис. 4.66 а). Используя токовую модель, находим, что поверхностный микроток протекает по боковой поверхности цилиндра с поверхностной плотностью j J . Направление плотности тока j показано на рис. 4.66 б.

Рис. 4.66. Постоянный магнит в виде цилиндра, намагниченного вдоль

образующей

Поле B внутри магнита находится как поле соленоида. Оно

однородное и равно

321

B 0 j 0J .

Так как B и J внутри магнита однонаправлены, то в векторной форме

B 0 J .

Поле H внутри магнита

69. Квазистационарные электромагнитные поля. Поверхностный

эффект. Граничное условие Леонтовича

Квазистационарным электромагнитным полем называют переменное во времени электромагнитное поле, в котором магнитное поле токов смещения существенно меньше магнитного поля токов проводимости и микротоков.

Этот факт зависит от частоты электромагнитного поля. Чем меньше частота,

тем с большей точностью электромагнитное поле можно считать квазистационарным. Установим порядок этих частот.

Плотность тока проводимости внутри проводника связана с напряженностью электрического поля законом Ома в дифференциальной форме

322

E .

Плотность тока смещения:

см D .t

В комплексной форме записи:

см j D j E .

Отношение амплитуд плотности тока смешения и плотности тока проводимости будет равно:

(реальные частоты гораздо ниже) электромагнитное поле в хорошо

Легко получить, что для квазистационарного электромагнитного поля запаздывающие электродинамические потенциалы (2.89) и (2.93)

превращаются в следующие выражения

323

Переходим к изучению явления поверхностного эффекта. Пусть на проводящее полупространство ( 0 , , ) падает плоская линейно поляризованная волна (рис. 4.67). Волна поляризована вдоль оси x и

распространяется вдоль оси z .

Рис. 4.67. Падение плоской волны на полупространство с параметрами , ,

В силу симметрии поле E внутри проводника также будет иметь только x -овую составляющую, а поле B соответственно только y -овую

составляющую.

Найдем, как изменяются поля E и B внутри проводника. Рассмотрим случай квазистационарного электромагнитного поля. Уравнения Максвелла в

комплексной форме запишем внутри проводящего полупространства:

Уравнения для дивергенций выполняются автоматически, так как

дивергенция ротора тождественно равна нулю, т.е.:

divB div j rotE j div rotE 0 .

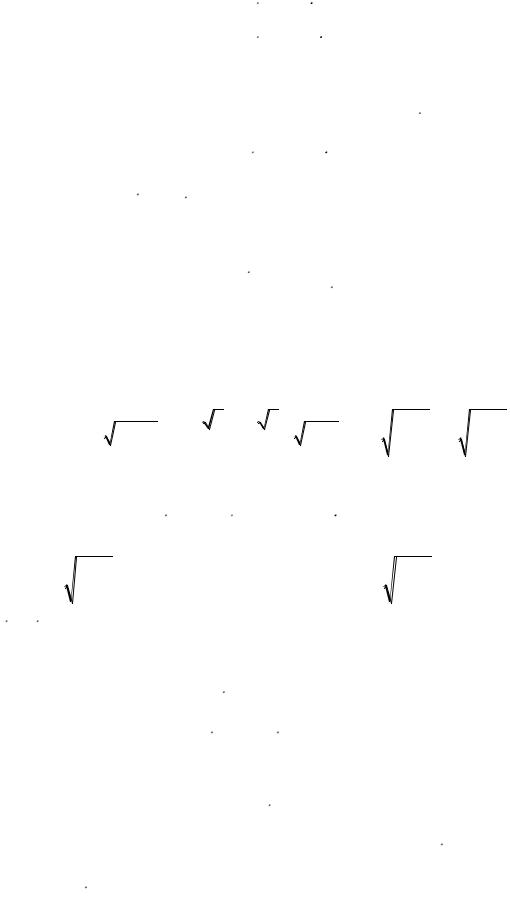
Подставляя (4.149) и (4.150) в (4.147), вместо выписанной системы

уравнений получим:

Общее решение дифференциального уравнения (4.153):

By z C1e j z C2e j z ,

C1 , C2 - комплексные постоянные.

Вследствие наличия тепловых потерь в проводнике при z поле должно исчезать. Поэтому C2 0 и

By z C1e ze j z .

Так как начальную фазу одной из физических величин можно выбрать произвольной, то примем число C1 вещественным и обозначим его через Bm

(ниже будет понятно, почему это так). Очевидно Bm By 0 . Тогда

By z Bme ze j z Bme z sin t z By z,t .

Это затухающая бегущая волна.