
- •Введение
- •Поверхности второго порядка История
- •Понятие поверхности второго порядка
- •Инварианты уравнения поверхности второго порядка.
- •Классификация поверхностей второго порядка
- •Эллипсоид.
- •Однополостный гиперболоид.
- •Двуполостный гиперболоид.
- •Эллиптический параболоид.
- •Гиперболический параболоид.
- •Конус второго порядка.
- •Эллипсоид
- •Свойства эллипсоида.
- •Форма эллипсоида.
- •Исследование формы поверхности второго порядка методом сечения плоскостями
- •Maxima– система компьютерной алгебры.
- •История.
Исследование формы поверхности второго порядка методом сечения плоскостями
Если
дано каноническое уравнение поверхности
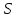 ,
то представление о поверхности можно
получить по форме линий пересечения ее
плоскостями:
,
то представление о поверхности можно
получить по форме линий пересечения ее
плоскостями:
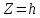 —параллельными
координатной плоскости
—параллельными
координатной плоскости
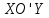 ,
,
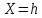 —параллельными
координатной плоскости
—параллельными
координатной плоскости
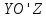 ,
,
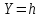 —параллельными
координатной плоскости
—параллельными
координатной плоскости
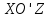 .
.
Пусть дан эллипсоид:
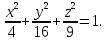
Это
эллипсоид в прямоугольной декартовой
системе координат
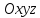 ,
где оси
,
где оси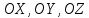 — оси симметрии.
— оси симметрии.
Рассмотрим линии
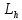 плоскостями
плоскостями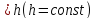 :
:
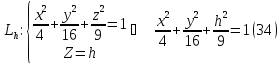
Плоскость
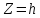 параллельна плоскости
параллельна плоскости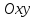 .
.
Уравнения
проекций
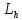 на
на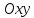 имеют вид:
имеют вид:
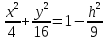
Если
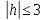 ,
то
,
то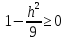 ,
и тогда поделим обе части уравнения на
,
и тогда поделим обе части уравнения на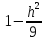 ,
получим:
,
получим:
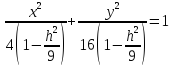
Это
уравнение эллипсов с полуосями
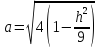 ,
,
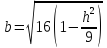 ;
увеличивающиеся с уменьшением
;
увеличивающиеся с уменьшением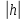 ,
центр эллипса-
,
центр эллипса-
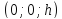
При
различных
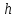 имеем:
имеем:
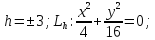
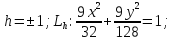
Если
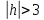 ,
тогда
,
тогда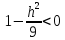 и значит линий
и значит линий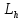 ,
удовлетворяющих уравнению
,
удовлетворяющих уравнению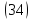 -
нет.
-
нет.
Рассмотрим
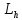 ,
полученные в сечениях эллипсоида
плоскостями
,
полученные в сечениях эллипсоида
плоскостями :
:
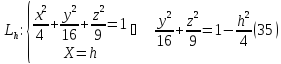
Уравнение
проекций
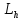 на
на .
.
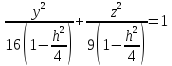
Это
уравнение эллипсов с полуосями
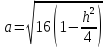 ,
,
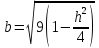 ;
;
Если
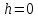 ,
то
,
то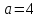 ,
,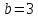 ,
и
,
и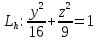
Если
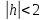 ,
тогда мы получаем семейство эллипсов:
,
тогда мы получаем семейство эллипсов:
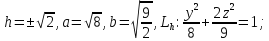
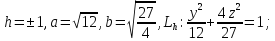
Если
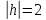 ,
тогда
,
тогда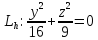 — это уравнение точки с координатами
— это уравнение точки с координатами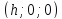 .
.
Если
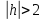 ,
тогда
,
тогда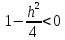 и значит линий
и значит линий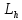 ,
удовлетворяющих уравнению
,
удовлетворяющих уравнению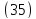 – нет.
– нет.
3.
Рассмотрим
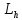 ,
полученные в сечениях эллипсоида
плоскостями
,
полученные в сечениях эллипсоида
плоскостями
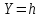 :
:
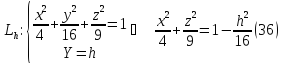
Уравнения
эллипсов, проекций
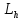 на
на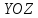 и имеют центры
и имеют центры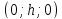 .
.
Полуоси
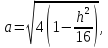
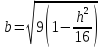 ,
,
Если
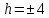 ,
тогда
,
тогда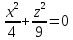 ,
уравнение точек с координатами
,
уравнение точек с координатами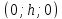 .
.
Если
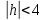 ,
тогда мы получаем семейство эллипсов:
,
тогда мы получаем семейство эллипсов:
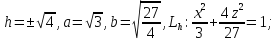
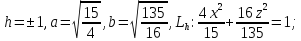
Если
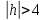 ,
тогда
,
тогда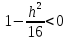 и значит линий
и значит линий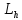 ,
удовлетворяющих уравнению
,
удовлетворяющих уравнению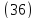 - нет.
- нет.
Вывод
Проанализировав
уравнение эллипсоида
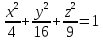 ,
получили некоторые представления о
форме эллипсоида.
,
получили некоторые представления о
форме эллипсоида.
Из
уравнения следует, что оси
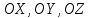 — оси симметрии, плоскости
— оси симметрии, плоскости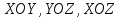 — плоскости симметрии.
— плоскости симметрии.
Рассекая
поверхность плоскостями
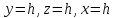 ,
в
сечениях имеем эллипсы, наибольшие из
которых получаются в плоскостях
,
в
сечениях имеем эллипсы, наибольшие из
которых получаются в плоскостях
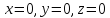 ,
полуоси их уменьшаются с увеличением
,
полуоси их уменьшаются с увеличением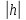 ,
вершины эллипсов имеют координаты
,
вершины эллипсов имеют координаты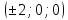 по оси
по оси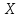 ;
;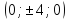 по оси
по оси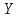 ;
;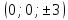 по оси
по оси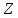 .
.
Maxima– система компьютерной алгебры.
Среди математического ПО для аналитических (символьных) вычислений наиболее широко известно коммерческое (Maple, Mathematica). Maxima - это очень мощный инструмент для ученого или преподавателя, аспиранта или студента, позволяющий автоматизировать наиболее рутинную и требующую повышенного внимания часть работы, оперирующий при этом аналитической записью данных, т.е. фактически математическими формулами. Такую программу можно назвать средой программирования, с той разницей, что в качестве элементов языка программирования выступают, привычные человеку, математические обозначения.
Программа, работает на тех же принципах и предоставляет похожий функционал; самое радикальное ее отличие – то, что она не является ни коммерческой, ни закрытой. Другими словами, речь идет о свободной программе. На самом деле использование свободного ПО более естественно для фундаментальной науки, нежели коммерческого, так как модель, которая используется в свободном ПО – это модель открытости и общедоступности всех наработок. Очевидно, эти же свойства присущи и результатам научной деятельности. Используя такую схожесть подходов, можно фактически рассматривать расширения функционала свободных программ или дополнительные библиотеки, которые могут создаваться для своих нужд в процессе научных исследований, как неотъемлемую часть результатов таких исследований. И эти результаты могут использоваться и распространяться на усмотрение пользователя без оглядки на ограничения, налагаемые лицензиями исходного ПО. В случае же коммерческого ПО, которое находится в собственности его производителя, такого рода свободы значительно ограничены, начиная от невозможности свободно (и законно) передавать само такое ПО вместе с наработками и вплоть до возможных патентных исков от компании-разработчика ПО в случае распространения самодельных дополнительных библиотек к нему.
С другой стороны, основное направление, кроме научных разработок, где такие программы востребованы – это высшее образование; а использование для учебных нужд именно свободного ПО – это реальная возможность и для вуза, и для студентов и преподавателей иметь в своем распоряжении легальные копии такого ПО без больших, и даже сколь-нибудь существенных, денежных затрат.
Моя дипломная работа и посвященна свободной программе аналитических вычислений Maxima.
В настоящее время Maxima — это система компьютерной математики, которая предназначена для выполнения математических расчетов (как в символьном, так и в численном виде) таких как:
упрощение выражений;
графическая визуализация вычислений;
решение уравнений и их систем;
решение обыкновенных дифференциальных уравнений и их систем;
решение задач линейной алгебры;
решение задач дифференциального и интегрального исчисления;
решение задач теории чисел и комбинаторных уравнений и др.
В системе имеется большое количество встроенных команд и функций, а также возможность создавать новые функции пользователя. Система имеет свой собственный язык. Она также имеет встроенный язык программирования высокого уровня, что говорит о возможности решения новых задач и возможности создания отдельных модулей и подключения их к системе для решения определенного круга задач.
