
закон Гука
.docМинистерство образования АР Крым
Таврический Национальный Университет им. Вернадского
Исследование физического закона
ЗАКОН ГУКА
Выполнил: студент 1 курса
физического факультета гр. Ф-111
Потапов Евгений
Симферополь-2010
План:
-
Связь между какими явлениями или величинами выражает закон.
-
Формулировка закона
-
Математическое выражение закона.
-
Каким образом был открыт закон: на основе опытных данных или теоретически.
-
Опытные факты на основе которого был сформулирован закон.
-
Опыты, подтверждающие справедливость закона, сформулированного на основе теории.
-
Примеры использования закона и учета действия закона на практике.
-
Литература.
Связь между какими явлениями или величинами выражает закон:
Закон Гука связывает такие явления, как напряжение и деформацию твердого тела, модуль силы упругости и удлинение. Модуль силы упругости, возникающей при деформации тела, пропорционален его удлинению. Удлинением называется характеристика деформативности материала, оцениваемая по увеличению длины образца из этого материала при растяжении. Си́ла упру́гости — сила, возникающая при деформации тела и противодействующая этой деформации. Напряжение — это мера внутренних сил, возникающих в деформируемом теле под влиянием внешних воздействий. Деформа́ция — изменение взаимного положения частиц тела, связанное с их перемещением друг относительно друга. Эти понятия связаны так называемым коэффициентом жесткости. Он зависит от упругих свойств материала и размеров тела.
Формулировка закона:
Зако́н Гу́ка — уравнение теории упругости, связывающее напряжение и деформацию упругой среды.
Формулировка закона - сила упругости прямо пропорциональна деформации.
Математическое выражение закона:
Для тонкого растяжимого стержня закон Гука имеет вид:
![]()
Здесь F сила натяжения стержня, Δl — его удлинение(сжатие), а k называется коэффициентом упругости (или жёсткостью). Минус в уравнении указывает на то, что сила натяжения всегда направлена в сторону, противоположную деформации.
Если ввести относительное удлинение

и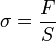 нормальное напряжение в поперечном
сечении
нормальное напряжение в поперечном
сечении
т![]() о
закон Гука запишется так
о
закон Гука запишется так
В такой форме он справедлив для любых малых объёмов вещества.
В общем случае напряжения и деформации являются тензорами второго ранга в трёхмерном пространстве (имеют по 9 компонент). Связывающий их тензор упругих постоянных является тензором четвёртого ранга Cijkl и содержит 81 коэффициент. Вследствие симметрии тензора Cijkl, а также тензоров напряжений и деформаций, независимыми являются только 21 постоянная. Закон Гука выглядит следующим образом:
![]()
где σij
— тензор
напряжений,
![]() —
тензор
деформаций.
Для изотропного материала тензор Cijkl
содержит только два независимых
коэффициента.
—
тензор
деформаций.
Для изотропного материала тензор Cijkl
содержит только два независимых
коэффициента.
Каким образом был открыт закон: на основе опытных данных или теоретически:
Закон был открыт в 1660 году английским учёным Робертом Гуком (Хуком) на основе наблюдений и экспериментов. Открытие, как утверждал Гук в своём сочинении «De potentia restitutiva», опубликованном в 1678, сделано им за 18 лет до этого времени, а в 1676 было помещено в другой его книге под видом анаграммы «ceiiinosssttuv», означающей «Ut tensio sic vis». По объяснению автора, вышесказанный закон пропорциональности применяется не только к металлам, но и к дереву, камням, рогу, костям, стеклу, шёлку, волосу и проч.
Опытные факты на основе которых был сформулирован закон:
История об этом умалчивает..
Опыты, подтверждающие справедливость закона, сформулированного на основе теории:
Закон сформулирован на основе опытных данных. Действительно, при растягивании тела (проволоки) с определенным коэффициентом жесткости k на расстояние Δl, то их произведение будет равно по модулю силе, растягивающей тело (проволоку). Такое соотношение будет выполняться, однако, не для всех деформаций, а для небольших. При больших деформациях закон Гука перестает действовать, тело разрушается.
Примеры использования закона и учета действия закона на практике:
Как следует из закона Гука, по удлинению пружины можно судить о силе, действующей на нее. Этот факт используется для измерения сил с помощью динамометра – пружины с линейной шкалой, проградуированной на разные значения сил.
Литература.
1. Интернет-ресурсы: - сайт Википедия (http://ru.wikipedia.org/wiki/%D0%97%D0%B0%D0%BA%D0%BE%D0%BD_%D0%93%D1%83%D0%BA%D0%B0).
2. учебник по физике Перышкин А.В. 9 класс
3. учебник по физике В.А. Касьянов 10 класс
4. лекции по механике Рябушкин Д.С.
