
Lektsii_Rubleva_1 / Гл 01 Вступ до анал_зу - копия / Пар 1-03 Упорядкован_ простори
.docВластивості доведено.
|
Теорема 4. |
(Топологічна властивість верхньої межі). |
|
|
Точка
|
Доведення.
Необхідність.
Нехай
![]()
![]()
![]() є мажорантою
є мажорантою
![]() ,
розглянемо довільний окіл
,
розглянемо довільний окіл
![]() цієї точки. Можливі три випадки.
цієї точки. Можливі три випадки.
-
 -
найбільша точка простору
-
найбільша точка простору
 ,
тоді
,
тоді

 .
З того, що
.
З того, що
 є найменшою мажорантою, то
є найменшою мажорантою, то
 не є мажорантою
не є мажорантою

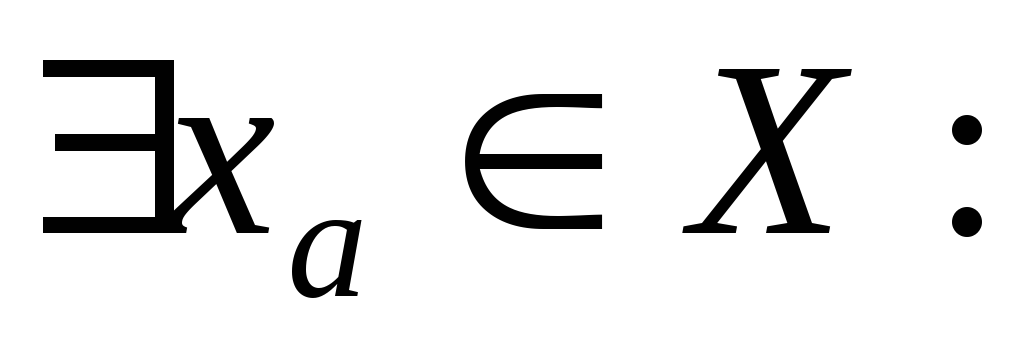






 є точкою дотикання.
є точкою дотикання. -
 -
найменша точка простору
-
найменша точка простору
 ,
за означенням верхньої межі та найменшої
точки ми маємо
,
за означенням верхньої межі та найменшої
точки ми маємо


 з аксіом часткового порядку
з аксіом часткового порядку


 є точкою дотикання
є точкою дотикання
 .
. -
Якщо
 довільна точка
довільна точка
 (ні найменша, ні найбільша), то
(ні найменша, ні найбільша), то


 оскільки
оскільки
 (бо
(бо
 не є мажорантою)
не є мажорантою)


 є точкою дотикання
є точкою дотикання
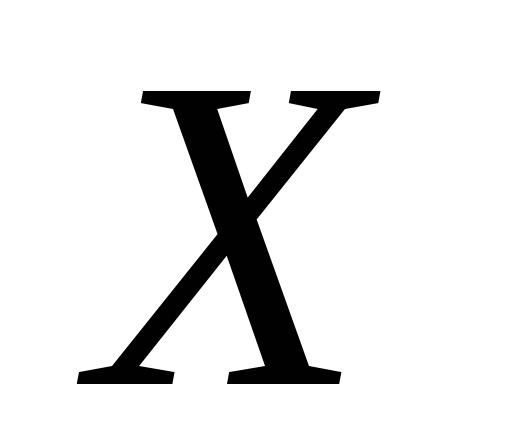 .
.
Необхідність доведена.
Достатність.
Нехай
![]() є мажорантою і точкою дотикання
є мажорантою і точкою дотикання
![]() .
Розглянемо
.
Розглянемо
![]() - множину всіх мажорант множини
- множину всіх мажорант множини
![]() .
Доведемо, що
.
Доведемо, що
![]() - найменший елемент
- найменший елемент
![]() .
Припустимо, що це не так, тобто
.
Припустимо, що це не так, тобто
![]() :
:
![]() ,
тоді правий промінь
,
тоді правий промінь
![]() є околом точки
є околом точки
![]() ,
а тому в ньому існує точка з
,
а тому в ньому існує точка з
![]() ,
але тоді ця точка більша за
,
але тоді ця точка більша за
![]() .
Але це неможливо, бо
.
Але це неможливо, бо
![]() ,
а тому є мажорантою
,
а тому є мажорантою
![]() ,
тому всі точки цієї множини не перевищують
,
тому всі точки цієї множини не перевищують
![]() .
Одержана суперечність завершує доведення
теореми.
.
Одержана суперечність завершує доведення
теореми.
Теорема доведена.
УП
![]() (або ЧУП) називається повним,
якщо в ньому кожна непорожня й обмежена
зверху множина має верхню межу.
(або ЧУП) називається повним,
якщо в ньому кожна непорожня й обмежена
зверху множина має верхню межу.
|
Теорема 5. |
(Повнота просторів дійсних чисел). |
|
|
УП
|
Доведення цієї теореми спирається знову таки на аксіоматику дійсних чисел, для доведення безпосередньо цього твердження нам потрібна аксіома повноти.
|
Аксіома. |
(Повнота або неперервність дійсних чисел). |
|
|
Якщо
|
Тепер
нам треба показати, що довільна не
порожня та обмежена зверху множина
![]() має супремум. Нехай
має супремум. Нехай
![]() - сукупність мажорант множини
- сукупність мажорант множини
![]() .
За умовою,
.
За умовою,
![]() ,
,
![]() .
З аксіоми повноти
.
З аксіоми повноти
![]() :
:
![]()
![]() .
Таким чином
.
Таким чином
![]() - мажоранта
- мажоранта
![]() та міноранта
та міноранта
![]() ,
але тоді
,
але тоді
![]() ,
але як міноранта
,
але як міноранта
![]() одночасно
одночасно
![]() - найменший елемент множини
- найменший елемент множини
![]() .
А тому
.
А тому
![]() .
.
Теорема доведена.
|
Приклад 11. |
Дуже
легко навести приклад неповного УП.
Розглянемо УП
|
|
Теорема 6. |
(Інфімум обмеженої знизу множини). |
|
|
У
повному УП
|
Доведення.
Позначимо таку множину
![]() ,
а через
,
а через
![]() позначимо множину її мінорант. Тоді
множина
позначимо множину її мінорант. Тоді
множина
![]() непорожня й обмежена зверху. З повноти
простору
непорожня й обмежена зверху. З повноти
простору
![]() існує
існує
![]() .
Доведемо, що
.
Доведемо, що
![]() .
.
Оскільки
![]()
![]() ,
то
,
то
![]() ,
а тому
,
а тому
![]() - є мінорантою множини
- є мінорантою множини
![]() .
Якщо
.
Якщо
![]() - інша міноранта множини
- інша міноранта множини
![]() ,
то
,
то
![]() і
і
![]() .
Отже
.
Отже
![]() є найбільшою мінорантою
є найбільшою мінорантою
![]() ,
а тому
,
а тому
![]() .
.
Теорема доведена.
|
Наслідок. |
(Повнота протилежного простору). |
|
|
Якщо
простір
|
Доведення безпосередньо слідує з теореми.
|
Теорема 7. |
(Найбільший елемент замкненої множини). |
|
|
У
повному УП
|
Доведення.
Оскільки
![]() - повний, то
- повний, то
![]() .
За теоремою 4
.
За теоремою 4
![]() є точкою дотикання
є точкою дотикання
![]() ,
а внаслідок її замкненості
,
а внаслідок її замкненості
![]() .
Але тоді за означенням
.
Але тоді за означенням
![]() - найбільший елемент.
- найбільший елемент.
Теорема доведена.
|
Наслідок. |
(Існування найменшого елементу замкненої множини). |
|
|
У
повному УП
|
