Lektsii_Rubleva_1 / Гл 01 Вступ до анал_зу - копия / Пар 1-03 Упорядкован_ простори

6

Глава 1

Вступ до аналізу

3. Упорядковані простори

Нехай задано множину . Бінарне відношення називається відношенням часткового порядку на множині , якщо виконуються такі умови (аксіоми):

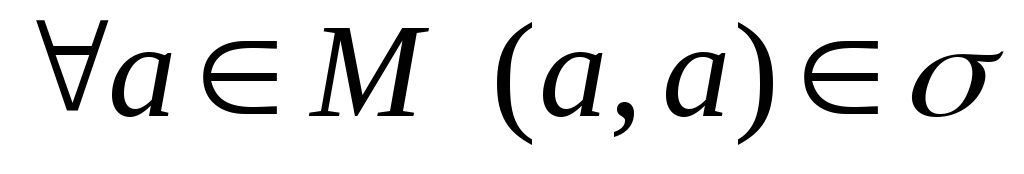1. (рефлексивність);

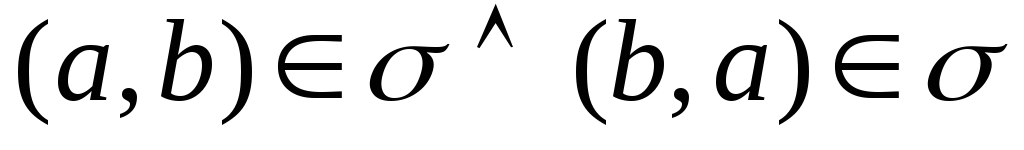
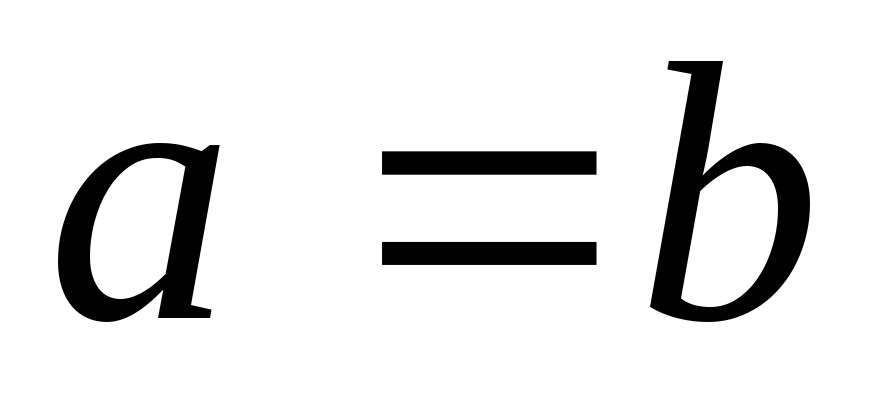2. (антисиметричність);

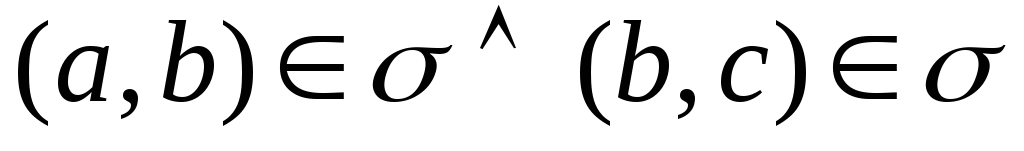
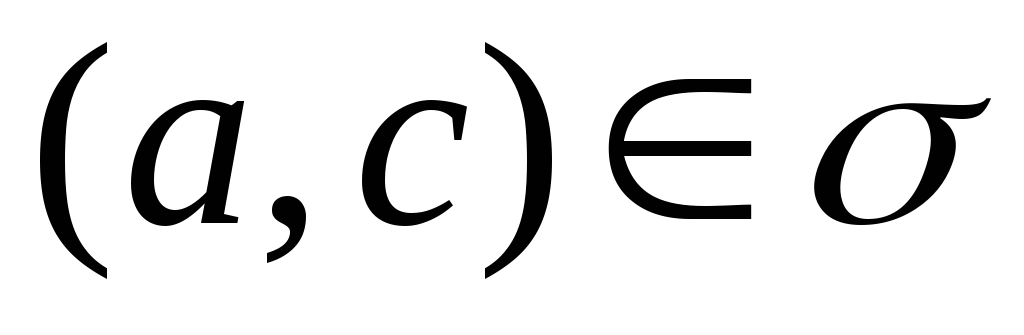3. (транзитивність).

Поряд з позначенням будемо також вживати позначення навіть, якщо частковий порядок не задається умовою “менше або дорівнює”.

Упорядкована пара (або ), яка складається з множини (основний простір) та відношення часткового порядку на ній називається частково упорядкованим простором (ЧУП), елементи множини - точками ЧУП. Точки називаються порівняними, якщо або , в протилежному випадку – непорівняними. Якщо ЧУП не містить непорівняних елементів, то він називається упорядкованим простором (УП), або лінійно упорядкованим простором.

Якщо - ЧУП, то очевидно, що обернене бінарне відношення є також відношенням часткового порядку, а ЧУП називається протилежним ЧУП по відношенню до і позначається .

Розглянемо УП і розширимо його за допомогою символів Продовжимо на цю множину відношення порядку менше або дорівнює та арифметичні дії. Розширену дійсну вісь позначимо . У випадках, коли байдуже яку з двох нескінченостей використовувати, будемо вживати символ просто . Тоді для точок з ми маємо такі визначення відповідних операцій:

1.	Якщо , то , , , мають в той самий зміст, що й в .
2.		3.
4.		5.
6.

Нехай - ЧУП, - деяка множина простору (тобто ). Елемент називається найбільшим (найменшим) елементом множини , якщо .

Зрозуміло, що навіть в УП зовсім не кожна множина має найбільший чи найменший елемент.

Спробуємо узагальнити поняття найбільшого та найменшого елементів.

Нехай - ЧУП, - деяка множина простору, елемент називається мажорантою (мінорантою) множини , якщо . Якщо множина має мажоранту (міноранту) вона називається обмеженою зверху (знизу). Множина, що обмежена зверху і знизу називається обмеженою. Найменша мажоранта (найбільша міноранта) множини , якщо вона існує називається верхньою (нижньою) межею множини , або супремумом (інфімумом) та позначається .

Зауважимо, що мінорантою (нижньою межею) множини в просторі є мажоранта (верхня межа) в просторі , тому з будь-якої властивості, що має місце для мажоранти легко сформулювати аналогічну, яка притаманна міноранті. Доведення робиться повністю аналогічно в просторі .

Розглянемо деякі властивості меж множин. Всі множини розглядаються в деякому ЧУП .

Теорема 1	(Зв’язок між найбільшим елементом та супремумом).
	Нехай найбільший елемент множини , тоді ця множина обмежена і .

Доведення. Оскільки - найбільший елемент, то обмежена зверху множина та її мажоранта. Якщо довільна мажоранта , але з того, що , тобто найменша мажоранта .

Теорема доведена.

Теорема 2	(Перехід до верхньої межі в нерівностях).
	Нехай . Якщо має верхню межу, то .

Доведення. - є мажорантою , а - найменша з мажорант, з чого безпосередньо слідує, що .

Теорема доведена.

Теорема 3	(Монотонність верхньої межі).
	Нехай . Якщо та мають верхні межі, то .

Доведення. Нехай , але ж за теоремою 2 .

Теорема доведена.

Визначимо в довільному ЧУП спеціальні множини, які нам добре відомі у випадку . Для їх кращого розуміння в довільному просторі, ми їх проілюструємо для двох прикладів. Будемо вважати, що в просторі параметри дорівнюють , а в просторі - .

Проміжок	Визначення
сегмент
інтервал
напівінтервали
ліві промені
праві промені

Якщо - найбільша (найменша) точка УП . Множина називається околом цієї точки, якщо . Якщо довільна точка (ні найменша, ні найбільша), то множина називається її околом, якщо .

Множина називається відкритою в просторі , якщо вона порожня, або є околом кожної своєї точки. Множина називається замкненою в просторі , якщо її доповнення є відкритою множиною.

Приклад 8.	Які з наведених множин є відкритими, замкненими в просторах , при умові, що ця множина належить основному простору?
		- відкр (відкр);		- замк. (замк. і відкр.);
		- ні (ні);		- замк. (замк.);
		- замк. (замк.);		- відкр. (не належить);
		- ні (відкр.);		- замк. (не належить);
		- замк. (замк);		- замк. і відкр. (замк. і відкр.).

Точка називається внутрішньою точкою множини , якщо є околом цієї точки. Точка є точкою дотикання (дотику) множини , якщо .

Приклад 9.	Які з наведених точок для множини є внутрішніми, точками дотику в просторі ?
Зрозуміло, що якщо точка внутрішня, то вона й дотикання, а тому можливі три випадки – дот (тільки дотикання), вн (внутрішня та дотикання), -(ні та, ні інша).
		вн	дот	дот	вн	-	вн	вн	-
		дот	дот	дот	дот	вн	вн	вн	вн
		дот	дот	дот	дот	дот	дот	дот	дот
		дот	дот	вн	вн	вн	вн	вн	вн
		дот	дот	дот	дот	вн	дот	дот	вн

Замиканням (внутрішністю) множини з УП називається сукупність її точок дотикання (внутрішніх точок) і позначається .

Приклад 10.	Для наведених множин побудувати замикання та внутрішність в просторі .
Множина	Замикання	Внутрішність

Наведемо деякі цікаві та дуже важливі властивості відкритих та замкнених множин.

Властивості.	(Критерії відкритих та замкнених множин).
1.	Множина відкрита тоді і тільки тоді, коли всі її точки внутрішні.
2.	Множина відкрита тоді і тільки тоді, коли .
3.	Множина замкнена тоді і тільки тоді, коли вона містить усі свої точки дотику.
4.	Множина замкнена тоді і тільки тоді, коли .

Доведення. 1-2. Необхідність. відкрита, тому для будь-якої точки вона є околом, тобто усі точки внутрішні. Достатність. Якщо всі точки внутрішні, то множина є околом кожної своєї точки, а тому є відкритою. Властивість доведена.

3-4. Необхідність. - замкнена, тобто її доповнення – відкрите. Якщо - точка дотику та не належить , то - відкритій множині, але тоді множині належить деякий окіл точки , а це суперечить тому, що вона є точкою дотику , тому що в її околі нема точок множини . Достатність. не є точкою дотику множини , а тому існує окіл , в якому нема точок множини , тобто - відкрита -замкнена.