
4_NeISV
.pdf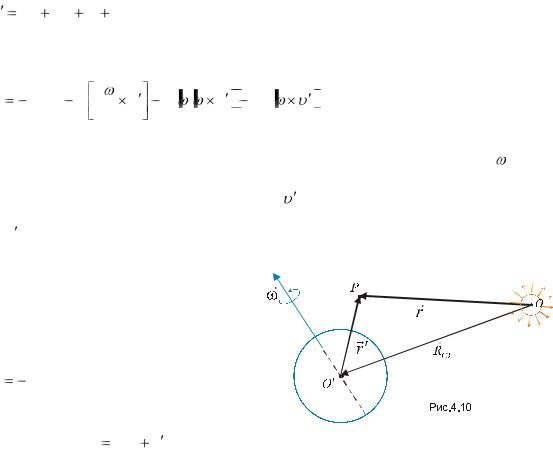
111
4.3. Рух частинки поблизу поверхні Землі
Уведення сил інерції дозволяє також досить просто пояснити цілу низку ефектів та явищ, що спостерігаються на поверхні Землі і зумовлені її неінерціальністю як системи відліку, тлумачення яких з точки зору ICB дуже складне і не наочне. Дійсно, Земля рухається відносно Сонця по еліптичній орбіті, тобто непрямолінійно і нерівномірно, а також обертається навколо осі, що походить через її центр, тобто поверхня Землі рухається прискорено відносно геліоцентричної системи відліку, яку ми в цьому випадку можемо вважати інерціальною без будь-яких застережень.
4.3.1. Рівняння руху частинки поблизу поверхні Землі
Поблизу поверхні Землі до частинки завжди прикладені сили гравітаційного притягання з
|
|
боку Землі FЗ |
та з боку Сонця FC , а також можуть бути прикладені інші сили взаємодії (сили |
тертя, опору середовища, взаємодії з іншими тілами окрім Землі та Сонця тощо), суму яких ми
позначимо як f . Тоді рівняння руху частинки відносно поверхні Землі можна записати так:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ma FЗ |
|
FС |
|
|
|
f |
Fін , |
|
|
|
|
|
|
|
|
|
|
(4.24) |
||||
причому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Fін |
mRСЗ |
m |
|
|
|
r |
m |
|
|
r |
2m |
|
|
, |
|
|
(4.25) |
|||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
де mRСЗ |
– поступальна сила інерції, обумовлена рухом Землі навколо Сонця, |
|
– кутова |
|||||||||||||||||||
швидкість |
обертання Землі навколо |
власної |
осі, |
|
– швидкість частинки відносно земної |
|||||||||||||||||
поверхні, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r – радіус-вектор частинки, що визначає її положення відносно центра Землі, в який ми |
||||||||||||||||||||||
вміщуємо початок HeICB (Рис. 4.11). |
|
|
|
|
|
|
|
|||||||||||||||
Гравітаційна сила, прикладена до частинки з |
|
|
|
|
|
|
|
|||||||||||||||
боку Сонця є |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mMС r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
FС |
G |
|
|
|
|
|
|
|
|
|
|
|
(4.26) |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.11 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
або, враховуючи, що r |
RСЗ |
r : |
|
|
|
|
|
|
|
|
|
|
||||||||||

112
|
|
|
|
|
|
|
|
|
|
|
|
|
mMC |
|
RСЗ |
r |
|
|
|||
FC |
G |
|
|
|
2 |
|
|
|
|
(4.27) |
|
|
|
||||||||
|
|
|
R |
r |
|
|
RСЗ |
r |
|
|
|
|
|
СЗ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
RЗ |
|
|
|
|
|
Величина |
|
|
r |
|
|
є порядку середнього радіуса Землі |
= 6370 км, а відстань від Землі до |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сонця |
RСЗ |
=1,5·10. Отже |
r |
|
|
|
RСЗ |
|
і можна з хорошою точністю вважати, що |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
mM |
C |
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
FC |
G |
|
|
|
|
|
СЗ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.28) |
|||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
R |
|
|
|
|
|
RСЗ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
СЗ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
З іншого боку, рівняння руху Землі під дією притягання Сонця, записане в геліоцентричній |
|||||||||||||||||||||||||||||||||
ICB має вигляд |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
M З МС RСЗ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
MЗ RСЗ |
|
|
G |
|
|
|
|
2 |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
(4.29) |
||||||
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
RСЗ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
СЗ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Із порівняння рівнянь (4.28) та (4.29) випливає рівність |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
FC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mRСЗ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.30) |
|||||
Після підстановки (4.30) в (4.24) з врахуванням (4.25) маємо |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
ma |
FЗ |
|
|
mRСЗ |
|
f |
|
|
|
mRСЗ |
m |
|
|
r |
m |
|
r |
2m |
|
|
. |
(4.31) |
|||||||||||
|
|
|
|
|
|
dt |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
У правій частині другий і четвертий доданки в сумі дають нуль. П’ятим доданком можна знехтувати, оскільки нерівномірність обертання Землі дуже мала: спостереження, що проводяться з
1995 р. за допомогою атомних годинників, показали, що коливання тривалості земної доби не перевищують 3 10-3 с за весь час спостережень. Отже обертання Землі можна вважати рівномірним
і покласти |
d |
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким чином, |
отримане рівняння руху частинки поблизу поверхні Землі можна подати у |
|||||||||||||
вигляді |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ma |
FЗ |
f |
m |
|
r |
2m |
|
|
, |
|
|
|
|
(4.32) |
причому для спрощення записів випущено штрихи в позначеннях величин, визначених |
||||||||||||||
відносно поверхні Землі, |
тобто замість |
|
|
|
|
|
|
|||||||
r , |
|
, a надалі будемо писати |
r , |
|
, a . Це не повинно |
|||||||||
викликати непорозумінь, оскільки надалі всі рухи розглядаються відносно поверхні Землі, а
штрихи будуть використовуватися лише в позначеннях величин, визначених відносно НеІСВ, що
рухаються прискорено відносно Землі.
113
4.3.2. Сила тяжіння поблизу поверхні Землі
Сила, яка завжди прикладена до тіла, що знаходиться поблизу поверхні Землі незалежно від того рухається воно чи ні, називається силою тяжіння поблизу поверхні Землі:
|
|
|
|
|
|
|
|
||
Fтяж |
FЗ |
m |
|
|
|
r . |
(4.33) |
||
Оскільки сила гравітаційної взаємодії частинки з Землею, яку в першому наближенні можна |
|||||||||
|
|
|
|
|
|
|
|
|
|
вважати кулею, |
FЗ |
залежить від r |
|
||||||
|
|
mM |
|
|
|
|
|
||
|
З r |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
FЗ |
G |
|
|
|
|
|
, |
|
(4.34) |
|
r 2 |
|
r |
|
|||||
а r |
RЗ |
|
h , |
|
|
|
|
|
|
|
то сила тяжіння |
Fтяж залежить і від висоти h над поверхнею Землі. Однак, |
|||||||
оскільки у переважній більшості практично важливих задач щодо руху тіл поблизу поверхні Землі
висота |
h |
не перевищує декількох десятків кілометрів, |
то нею можна нехтувати порівняно із |
|||||||||||||
середнім радіусом Землі RЗ |
і вважати, що r |
RЗ . Тоді величину сили гравітаційної взаємодії з |
||||||||||||||
Землею можна подати як |
|
|
|
|
|
|
|
|
|
|
|
|||||
FЗ |
G |
mM З |
|
|
(4.35) |
|
|
|
|
|
|
|
|
|||
R2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
З |
|
|
|
|
|
|
|
|
|
|
|
|
|
або |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
FЗ |
mg 0 , |
|
|
|
(4.36) |
|
|
|
|
|
|
|
||||
де g |
0 |
G M З |
9,83 м/с2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
RЗ2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
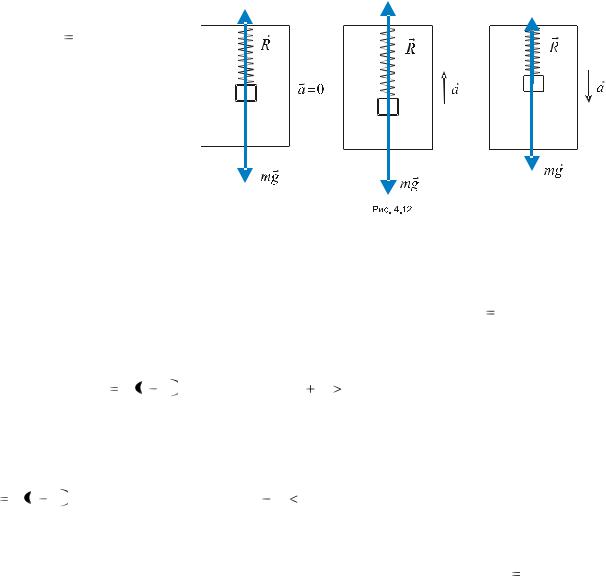
Оскільки відцентрова |
сила |
інерції |
|
|
|
|
|
|
|
|||||||
направлена |
перпендикулярно |
до |
осі |
|
|
Рис. 4.12 |
|
|
||||||||
обертання |
і |
в |
загальному |
випадку |
не |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
співпадає за напрямом з FЗ (Рис.4.12), то сила Fтяж не направлена точно до центру Землі, однак |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кут |
Fтяж |
^ FЗ |
є дуже малим. Обчислимо модуль сили тяжіння Fтяж та кут . |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Модуль вектора Fтяж за означенням є |
|
|
|
|
|
|
|
|||||||||
F |
|
|
|
|
|
|
|
|
|
|
|
2 |
2F F відц |
|
|
|
|
F |
|
F |
F |
F |
відц |
F |
F відц |
F 2 |
F відц |
|
cos F ^ F відц |
||||
|
тяж |
тяж |
тяж |
З |
ін |
З |
ін |
З |
ін |
|
З ін |
З |
ін |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.37) |

114
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Врахуємо, що cos F ^ F відц |
cos |
|
cos , де |
|
– географічна широта місцевості, |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
З |
|
|
ін |
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
F |
відц |
m |
|
2 R |
З |
cos |
. Підставляючи |
ці вирази разом з |
виразом |
(4.36) |
для |
FЗ отримаємо |
||||||||||||||||
|
ін |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
остаточно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
F |
|
m |
|
g |
2 |
|
4 R2 cos2 |
|
2g |
o |
|
2 R cos2 |
|
|
|
|
|
(4.38) |
||||||||
|
|
|
|
тяж |
|
|
|
|
|
o |
|
З |
|
|
|
|
|
|
З |
|
|
|
|
|
|
||||
|
|
Величину |
|
|
2 R |
З |
cos можна вважати малою порівняно з |
g |
0 |
. Дійсно, Земля здійснює повний |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
оберт відносно ―нерухомих‖ зірок за 86164 с, що відповідає кутовій швидкості |
1,16 10-5с-1 . |
||||||||||||||||||||||||||||
Отже максимальне значення відповідного відцентрового прискорення |
2 RЗ |
7,3 |
10 -2 м с 2 , що |
||||||||||||||||||||||||||
на 4 |
порядки менше за g |
0 |
. Тому, |
нехтуючи доданком з |
4 |
|
і застосовуючи відому формулу |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
x |
2 |
|
1 |
x , отримаємо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
m g |
o |
|
R |
2 cos 2 |
або |
F |
|
|
mg , |
|
|
|
|
|
(4.39) |
|||||||||
|
|
|
|
тяж |
|
|
|
|
З |
|
|
|
|
|
тяж |
|
|
|
|
|
|
|
|
||||||
|
|
де введено величину |
|
g |
g |
o |
R |
З |
2 cos 2 , яка називається прискоренням вільного падіння |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(більш точно модулем вектора прискорення вільного падіння) поблизу поверхні Землі і яка чисельно дорівнює
g 9,83 - 0,03 cos 2 |
м с 2 |
|
|
|
|
(4.40) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Кут між напрямом |
g |
|
|
|
Fтяж |
та напрямом |
go |
|
|
|
FЗ , тобто напрямом до центру Землі може |
бути знайдений за теоремою синусів
sin |
|
F відц |
|
m |
2 R |
З |
cos |
|
|
|
ін |
|
|
|
|
(4.41) |
|
sin |
|
Fтяж |
|
|
mg |
|||
|
|
|
|
|||||
звідки
2 RЗ |
sin 2 |
(4.42) |
|
2g |
|||
|
|||
Однак Земля, насправді, не є ідеальною кулею, а подібна до кулі сплюснутої в напрямку осі обертання. Ця сплюснутість пов’язана з відцентровою силою інерції (див. опис демонстраційного досліду, зображеного на Рис. 4.10), яка змусила речовину в пластичному незатверділому стані на ранніх стадіях існування Землі прийняти форму сфероїда, фігури близької до еліпсоїда обертання.
Полярна вісь цього еліпсоїда (та що проходить через полюси) на 1/300 коротша за його екваторіальну вісь. В дійсності так звана фігура Землі ще складніша. Це призводить до того, що

115
ефект зменшення прискорення вільного падіння g і сили тяжіння Fтяж при переміщенні по
поверхні Землі від полюса до екватора виявляється ще більш істотним. У зв’язку з цим експериментальна залежність прискорення вільного падіння дещо відрізняється від залежності
(4.40) отриманої вище без врахування відхилень фігури Землі від кулі:
g 9,83 - 0,05 cos2 м с |
2 |
|
(4.43) |
Зміна прискорення вільного падіння, а отже сили тяжіння при переміщенні з полюсів на екватор складає близько 0.06%. Максимальне відхилення напряму виска від напряму до центра Землі сягає 11 кутових мінут поблизу широти  45°.
45°.
Зміна сили тяжіння з широтою місцевості відбивається на результатах зважування тіл на пружинних терезах, оскільки нерухомі відносно поверхні Землі пружинні терези безпосередньо вимірюють суму всіх сил, прикладених до тіла (звичайно, окрім сили, прикладеної до тіла з боку самих терезів). Щоправда максимальна різниця результатів зважування одного й того ж самого тіла на полюсі і на екваторі становить всього 6 грамів на 1 кг. На практиці більш поширені терези з коромислом, зважування на яких зводиться до порівняння сил притягання до Землі двох тіл. Природно, що в цьому випадку результат не залежить від величини g в місці зважування.
Більш істотний вплив справляє широтна залежність прискорення вільного падіння на хід баштових та настінних годинників з гравітаційним маятником, період коливань якого визначається формулою
T |
|
l |
, |
(4.45) |
|
g |
|||
|
|
|
|
|
де l |
– довжина маятника, а g – прискорення вільного падіння. |
|
||
При переміщенні з полюса на екватор такі годинники почнуть відставати на 3,5 хвилин за добу! У
сучасних механічних годинниках використовується маятник Ґюйгенса, період коливань якого визначається його моментом інерції та коефіцієнтом закручування підвісу і, звичайно, не залежить від g .
Зазначені ―шкідливі‖ ефекти пов’язані зі зміною g при зважуванні на пружинних терезах або при
застосуванні гравітаційних маятників в годинниках, мають корисне застосування в приладах, що
називаються гравіметрами, за допомогою яких можна вимірювати прискорення вільного падіння в різних точках земної поверхні з високою точністю. Необхідність таких вимірів зумовлена тим, що Земля не є однорідне тіло. Тому поряд з нормальною широтною зміною прискорення вільного падіння, мають місце і аномалії сили тяжіння, величина яких досягає 0.05% від g , що на порядок менше його нормальної зміни.

116
Існує спеціальна наука – гравіметрія, дані якої широко використовуються в геології для розвідки корисних копалин. В останні десятиріччя цінну інформацію про неоднорідність сили тяжіння поблизу поверхні Землі отримано шляхом точного вимірювання траєкторій низькоорбітальних штучних супутників Землі лазерними далекомірами, які забезпечують точність порядку 1 см.
4.4. Вага тіла, невагомість, перевантаження
|
|
, тіла, що знаходиться в спокої відносно поверхні |
Оскільки прискорення a та швидкість |
|
Землі дорівнюють нулю, то рівняння руху (4.33) набуває вигляду
0 Fтяж |
R |
. |
(4.46) |
|
|
На підставі рівняння (4.46) можна сказати, що сила тяжіння Fтяж , прикладена до тіла,
врівноважується сумарною силою реакції R зв’язків, що обмежують рух тіла (опори, підвіси тощо). За третім законом Ньютона тіло діє на зв’язок або на сукупність зв’язків з рівною за модулем, але протилежно направленою силою. Цю силу називають вагою тіла .
Отже, вага тіла – це сила, з якою тіло діє на зв’язки.
Легко бачити, що для тіла, що знаходиться в спокої відносно поверхні Землі вага в точності
|
|
дорівнює силі тяжіння, оскільки за третім законом Ньютона P |
R , а відповідно до (4.46) |
R Fтяж . При цьому треба усвідомлювати, що сила тяжіння прикладена до розглядуваного
тіла, а вага тіла — це сила, прикладена з боку тіла до зв’язків (до опор, підвісів тощо). Ця відмінність між силою тяжіння і вагою особливо яскраво виявляється у випадку, коли сам зв’язок разом із тілом рухається прискорено відносно Землі. Рівняння руху для цього випадку запишемо у вигляді
|
|
|
|
|
ma |
Fтяж |
R , |
|
(4.47) |
|
|
|
|
– прискорення тіла разом із зв’язком відносно Землі. При цьому ми |
де R – реакція зв’язку, |
a |
|||
знехтували |
силою Коріоліса. |
Дійсно, навіть при швидкості тіла =1000 м с 1 максимально |
||
можливе значення сили Коріоліса не перевищує 0,1% від величини сили тяжіння Fтяж .
З рівняння (4.47) відповідно до означення разом із зв’язком:
|
|
|
|
|
|
|
P |
R |
ma |
Fтяж |
або P |
m g |
a |
отримуємо вагу тіла, що прискорено рухається
(4.48)
117
Остання формула визначає вагу тіла в загальному випадку. Видно, що вага тіла може
змінюватись залежно від величини і напрямку прискорення a .
Якщо вага перевищує за модулем величину mg , яку можна назвати нормальною вагою, то
кажуть, що має місце перевантаження. Перевантаження вимірюють відношенням дійсної ваги до нормальної, тобто в одиницях g : наприклад, перевантаження 10 g означає, що дійсна вага тіла є
більша за нормальну в 10 разів. |
|
|
Якщо ж P 0 , то кажуть, що |
|
|
тіло знаходиться |
в стані |
|
невагомості. |
|
|
Найпростіші |
і найбільш |
|
наочні приклади перевантажень |
|
|
|
|
|
та невагомості дають швидкісні |
Рис. 4.13 |
|
|
|
|
ліфти (Рис. 4.13). |
|
|
|
|
|
Коли ліфт знаходиться в спокої або |
рухається |
рівномірно, на пружину динамометра |
|||
|
|
|
|
|
|
прикріпленого до стелі кабіни з боку пробного тіла маси m прикладена сила P |
mg . |
||||
|
|
|
направленим угору, то до пружини з боку тіла |
||
Коли ліфт рухається з прискоренням a |
|||||
|
|
|
|
mg , тобто має місце перевантаження або |
|
прикладена сила P |
m g |
a , модуль якої є m(g a) |
|||
зростання ваги тіла, що супроводжується збільшенням розтягу пружини.
|
|
|
|
|
|
|
Коли ліфт рухається з прискоренням a |
направленим униз, то до пружини прикладена сила |
|||
|
|
|
a) mg . Розтяг пружини при цьому |
менший за |
|
P |
m g |
a , модуль якої тепер є m(g |
|||
нормальний: іноді кажуть про втрату ваги. |
|
|
|
||
|
|
|
|
|
|
|
Нарешті, при вільному падінні ліфта (що для ліфта означає аварію), маємо a |
g |
і сила P , з |
||
якою тіло діє на зв’язок (пружину) дорівнює нулю: для тіла виникає стан невагомості.
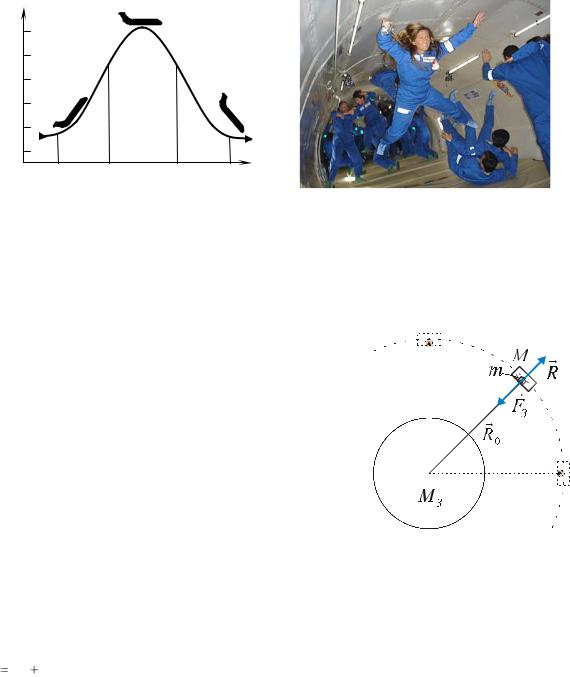
У цьому прикладі перевантаження і невагомість виникають при поступальному переміщенні зв’язку (підвісу) і можуть бути інтерпретовані як наслідок дії поступальної сили інерції. (Рекомендуємо читачу отримати самостійно наведені вище результати, розглянувши рух тіла маси m в HeICB, зв’язаній з ліфтом).

118
Значні перевантаження можуть виникати і при рівномірному русі по криволінійній траєкторії.
Оцінимо вагу пілота і перевантаження при виконанні літаком так званої ―мертвої‖ петлі (політ по коловій
траєкторії, що лежить у вертикальній площині(Рис. 4.14)) у різних точках траєкторії.
Для визначеності приймемо швидкість літака |
200 м / с , радіус петлі r 1000 м . |
|
|
Застосуємо наведене вище означення ваги: P |
R . |
Рівняння руху пілота в системі відліку, пов’язаній з поверхнею Землі, яку в цій задачі з хорошим наближення можна вважати інерціальною, запишеться як
|
|
|
ma |
mg |
R , |
де m – маса пілота, а R – сумарна сила реакції,
прикладена до пілота з боку зв’язків (крісло, прив’язані ремені тощо).
A
R ө
|
|
|
|
n |
|
|
|
|
|
mg |
(4.49) |
O |
|
|
|
C |
r
Отже, |
знову |
маємо |
|
|
|
|
|
|
|
Оскільки |
літак |
|
B |
|
|
|
|
|||||||||||||||||||||
P |
|
m g |
a . |
Рис. 4.14 |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
рухається по колу рівномірно, то прискорення пілота має лише нормальну складову |
a |
|
n і таким |
|||||||||||||||||||||||||||||||||||
r |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
чином, |
P |
m g |
|
|
|
|
n . Внаслідок зміни напряму n , вектор P буде змінюватись як за напрямом, так і за |
|||||||||||||||||||||||||||||||
|
|
r |
||||||||||||||||||||||||||||||||||||
модулем. |
Останній є |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
g 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
P |
m |
|
P P |
|
m |
|
|
|
|
|
|
2 |
|
|
|
g cos |
, |
|
|
|
|
|
|
|
||||||||||||||
|
|
r |
|
r |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а косинус кута між напрямом вектора P та напрямом вектора g є |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
g |
|
|
|
cos |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
Pg |
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
cos |
g ^ P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|||||
|
|
Pg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g 2 |
|
|
|
|
|
|
|
2 |
|
|
g cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
де |
|
g ^ n |
|
– кут між вектором n нормалі до траєкторії та напрямом вектора g . |
|
|
|
|||||||||||||||||||||||||||||||
У |
|
|
найвищій |
|
|
|
|
точці |
|
|
|
траєкторії |
A |
маємо |
кут |
0 |
|
і, |
|
відповідно, |
||||||||||||||||||
|
|
|
(g |
|
2 |
|
r) |
|
g |
2 |
r |
|
1 , |
оскільки |
|
2 r |
|
|
|
антипаралельні. При |
||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
cos g ^ P |
|
|
|
|
|
|
g , тобто вектори g |
та P |
||||||||||||||||||||||||||||||
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
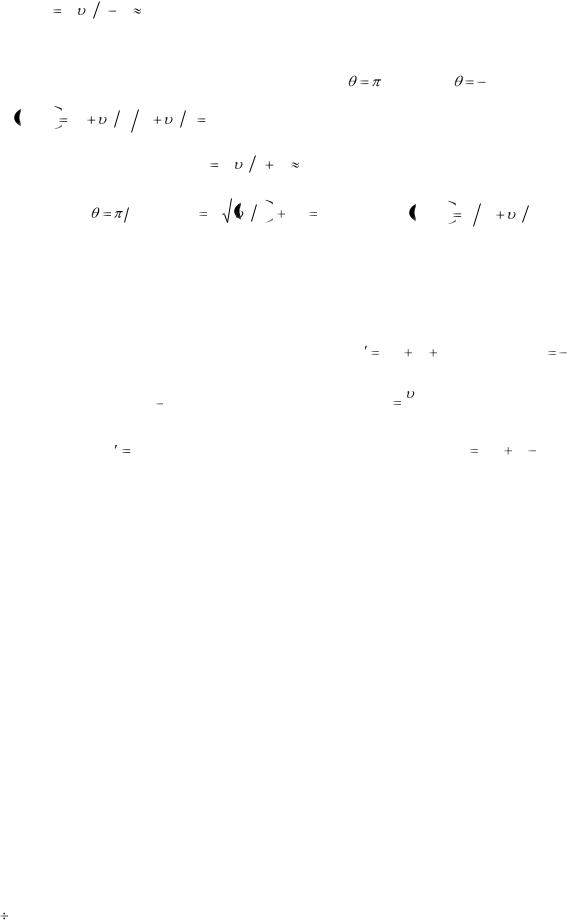
119
цьому P m |
2 |
r g |
3,18 mg , тобто пілота притискає до крісла з потрійним перевантаженням |
A |
|
|
|
направленим протилежно напряму нормального прискорення вільного падіння.
У |
|
найнижчій |
точці |
|
траєкторії |
|
B |
|
|
кут |
, |
|
|
cos |
1, |
і, |
|
|
відповідно, |
|||||||||
|
|
(g |
2 |
r) |
|
g |
2 |
r |
|
|
|
|
|
|
|
|
|
та |
|
співпадають і вага тут найбільша: |
||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
cos g ^ P |
|
|
1 , тобто напрями векторів g |
P |
||||||||||||||||||||||||
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
пілота притискає до крісла з силою P |
m |
|
r g |
|
5,1 mg (п’ятиразове перевантаження). |
|
|
|
||||||||||||||||||||
2 |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У точці C |
|
2 , отже |
P |
m |
2 |
r |
2 |
|
g 2 4,2 mg , а |
|
|
g |
|
g |
2 |
r |
|
. |
||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
cos g ^ P |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
Виникненню перевантажень можна надати інше пояснення. Оберемо систему відліку зв’язану з літаком, початок якої співпадає з центром мас літака. Вона є неінерціальною, оскільки рухається прискорено по криволінійній траєкторії (по колу). Якщо вона рухається поступально відносно ІСВ, то
рівняння руху |
пілота |
в |
цій |
|
|
|
|
де |
|
|
|
— |
|
системі відліку має вигляд ma |
mg |
R |
F пост , |
F пост |
ma |
||||||||
|
|
|
|
|
|
|
|
ін |
|
ін |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
поступальна сила інерції, |
a |
прискорення літака відносно ICB, |
a |
|
n . Оскільки пілот не рухається |
||||||||
r |
|||||||||||||
|
|
0 . У результаті рівняння руху пілота набуває вигляду 0 |
|
|
|
|
|
||||||
відносно літака, |
то a |
mg |
R |
ma , |
тобто є |
||||||||
тотожним до рівняння (4.49) і, звичайно, має такі ж самі розв’язки. Отже, при такому виборі системи відліку можна говорити, що перевантаження викликане поступальною силою інерції.
Обравши іншу HeICB, наприклад, початок якої лежить у центрі колової траєкторії літака, і яка обертається разом із радіус-вектором літака відносно цього початку, можна інтерпретувати виникнення перевантаження як наслідок дії на пілота відцентрової сили інерції.
Перевантаження, що виникають при польоті літаків та ракет можуть призвести до виходу з ладу апаратури, до руйнування конструкцій літального апарату та до загибелі пілота. Негативний вплив перевантажень на організм, пов’язано не з недостатньою міцністю кістяка людини, як іноді помилково вважають, а з поведінкою рідин, що містяться в організмі. Наприклад, відтік крові, що виникає в напрямку перевантаження, призводить до крововиливів в одних органах та до недостатнього надходження крові до інших. Особливо небезпечні відтоки та притоки крові до голови, оскільки серце нездатне забезпечити нормальний тиск. Тому розміщення тіла пілота надзвукового літака або космічного корабля перпендикулярно очікуваному напрямку перевантаження значно підвищує здатність організму витримувати перевантаження. Для тренованих пілотів вважаються припустимими короткочасні перевантаження порядку
6 7g .
120
Цілком зрозуміло, що добираючи швидкість і кривину траєкторії літака можна досягти ситуації, коли для предметів у кабіні буде мати місце стан невагомості. Дійсно, в спеціально обладнаних літаках можна
створити стан невагомості протягом декількох десятків секунд (Рис. 4.15), але дотримання необхідних для цього швидкості і траєкторії польоту потребує неабиякої майстерності пілотів.
h, км
10 |
|
9,5 |
|
9 |
|
8,5 |
|
8 |
невагомість |
7,5 |
|
0 20 45 65 t, c
Рис. 4.15
4.5. Невагомість в орбітальній станції
На відміну від ліфта і літака стан невагомості в космічних апаратах може існувати роками і
не потребує ніяких зусиль для його підтримання. Розглянемо найпростіший і практично важливий випадок невагомості в орбітальній станції, що рухається навколо Землі по коловій орбіті так, як показано на Рис. 4.16, тобто весь час вона звернута до Землі однією стороною. У цій задачі можна вважати систему
відліку з початком у центрі Землі, яка рухається поступально,
інерціальною, оскільки прискорення орбітальної станції
 Рис. 4.16
Рис. 4.16
відносно Землі є набагато більшим за прискорення центру Землі
відносно коперникової ICB. Рівняння руху маленького пробного тіла маси m , що знаходиться в спокої всередині станції є
|
|
|
|
ma |
FЗ |
R , |
(4.50) |
|
|
|
|
|
|
|
|
де враховано |
силу |
притягання Землі FЗ |
та можливу реакцію R |
з |
боку орбітальної станції. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Прискорення |
a |
тіла |
m відносно ICB співпадає з прискоренням станції |
Ro |
відносно центра Землі. |
||
Останнє легко знайти з рівняння руху станції
