
4_NeISV
.pdf
Розділ 4
РУХ ВІДНОСНО НЕІНЕРЦІАЛЬНИХ СИСТЕМ ВІДЛІКУ
Інерціальні системи відліку досить зручні для розв’язування різноманітних задач механіки.
Їх перевага перед іншими системами відліку полягає насамперед у тому, що перебіг усіх механічних явищ у них є однаковий.
Але далеко не всі системи відліку, відносно яких доводиться розглядати рух на практиці, є
інерціальні: ми вже зауважували, що найбільш широко вживана система відліку, пов’язана з поверхнею Землі може вважатись інерціальною лише наближено. Ще більш далекими від інерціальних, але практично дуже важливими є системи відліку пов’язані з транспортними засобами: кораблями, ракетами, літаками тощо. З викладеного у попередньому розділі випливає,
що основне рівняння динаміки матеріальної точки, за допомогою якого можна розв’язувати надзвичайно широке коло задач динаміки в ICB, не залишається незмінним при переході до
HeICB, внаслідок того, що прискорення відносно HeICB не співпадає з прискоренням відносно
ICB. Отже для того, щоб з’ясувати як перетворюється основне рівняння динаміки при переході від
ICB до HeICB в першу чергу необхідно знайти зв’язок між векторами прискорень частинки відносно ICB та HeICB.
4.1. Зв’язок між векторами швидкості та прискорення відносно ICB та HeICB
При розгляді цього питання і надалі в цьому розділі будемо вважати, що всі припущення за яких розглядався перехід від однієї ICB до іншої (див.3.5), а саме: незмінність довжин
просторових відрізків ( l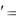 l ), плину часу ( t
l ), плину часу ( t t ), маси m
t ), маси m m
m та взаємодії з іншими
та взаємодії з іншими
тілами та полями ( F F ) , залишаються в силі і при переході від деякої ICB K до HeICB K .
Нехай система K рухається довільним чином відносно системи K , тобто прискорено
рухається довільним чином відносно системи K , тобто прискорено
переміщується і обертається навколо деякої осі з кутовою швидкістю . Для наочності будемо
вважати, що ICB — це коперникова система відліку, початок якої O лежить у центрі Сонця, а
HeICB — система відліку, зв’язана з Землею, що обертається навколо своєї осі та переміщується
як ціле відносно Сонця (Рис. 4.1), причому початок її O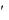 лежить у центрі Землі.
лежить у центрі Землі.

102
Опишемо рух однієї і тієї ж частинки P у системах відліку K та K .
Положення частинки P в HeICB
визначається радіус-вектором r , а в ICB –
радіус-вектором r . Положення початку
O системи K відносно початку O
відносно початку O
системи K визначається радіус-вектором
R . Очевидний зв’язок між цими векторами дає формула
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.1 |
|
|||||||
|
|
|
|
(4.1) |
|
|
|
|
|
|
|
|
|
|
|
||||||||
r R |
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Швидкість частинки P відносно ICB K знайдемо як похідну від радіус-вектора за часом t : |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dr |
|
|
dR |
|
dr |
|
|
(4.2) |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
dt |
|
dt |
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Розглянемо детально обчислення похідних у правій частині (4.2). |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Радіус-вектор R можна подати у вигляді |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
Xi |
Yj |
Zk |
|
|
|
(4.3) |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
де i , j , k є орти декартової системи координат, жорстоко зв’язаної з системою відліку K . |
|||||||||||||||||||||||
Тоді |
|
швидкість |
початку |
O |
відносно |
початку |
O |
відповідно до |
відомих правил |
||||||||||||||
диференціювання суми та добутку є |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
dR |
|
|
|
|
|
di |
|
dj |
|
dk |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
V |
|
|
|
|
|
Xi |
|
Yj |
Zk |
Xi |
Yj |
Zk |
X |
|
|
Y |
|
Z |
|
|
(4.4) |
||
|
dt |
|
|
dt |
|
dt |
dt |
dt |
|||||||||||||||
Останні три доданки в цьому виразі дорівнюють нулю, оскільки дорівнюють нулю похідні за часом від ортів, напрямки яких є незмінними відносно системи K . Отже,
|
|
|
|
(4.5) |
V |
Xi |
Yj |
Zk |
|
|
|
|
|
|
|
|
|
|
|
|
|
Радіус-вектор r |
можна розкласти по ортам i , j , k |
декартової системи координат жорстко |
||||
зв’язаної з системою K . |
|
|
|
|||
|
|
|
|
|
|
|
r |
x i |
y j |
z k |
|
|
(4.6) |
Похідна від r за часом t є

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
103 |
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
dr |
|
|
|
|
dy |
|
dz |
|
di |
|
dj |
|
|
dk |
|
|
|
||||||||||
|
|
|
|
|
|
i |
|
|
|
|
|
j |
|
|
|
k |
x |
|
y |
|
|
z |
|
|
|
|
|
(4.7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
dt |
|
|
dt |
|
|
|
dt |
|
|
dt |
|
|
dt |
|
dt |
|
|
dt |
|
|
|
||||||
Оскільки |
t |
|
t , то в перших трьох доданках (4.7) замінимо dt |
на dt |
, і позначимо їх суму |
|||||||||||||||||||||||
як : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
dy |
|
|
|
dz |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
i |
|
|
|
|
j |
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
(4.8) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
dt |
|
dt |
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Ми бачимо, що всі величини в правій частині (4.8) визначені виключно відносно системи |
||||||||||||||||||||||||||||
відліку K і вектор |
|
є, таким чином, вектор швидкості частинки A відносно HeICB K . |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Похідні від ортів |
i |
, j , k |
взяті за часом |
t |
у правій частині формули (4.7) у загальному |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
випадку не дорівнюють нулю, |
оскільки ці орти на відміну від ортів |
i |
, j , k при обертанні |
|||||||||||||||||||||||||
системи K змінюють свою орієнтацію відносно системи K . Виходячи із тих самих міркувань,
змінюють свою орієнтацію відносно системи K . Виходячи із тих самих міркувань,
що й при отриманні другого доданку у формулі (2.40), для цих похідних можна записати вирази
|
|
di |
|
|
|
i |
, |
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
, |
|
|
|
|
|
(4.9) |
|
|
dj |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k . |
|
|
|
|
|
|
|
|
|
dk |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
Підставляючи (4.8) та (4.9) у (4.7) і використовуючи розподільчу властивість векторного |
||||||||||||
добутку отримаємо |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dr |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
r |
|
|
. |
|
|
|
(4.10) |
|
|
dt |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким чином, швидкості та |
частинки P відносно системи K та відносно системи K , |
|||||||||||
відповідно, зв’язані співвідношенням |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
. |
|
|
(4.11) |
|
|
|
|
V |
|
|
r |
|
|
|
|
||
|
Вектор |
називають абсолютною швидкістю частинки |
A , вектор |
її відносною, а вектор |
|||||||||
|
|
|
її переносною швидкістю. |
|
|
|
|||||||
V |
|
|
r |
|
|
|
|||||||
|
Диференціюванням вектора абсолютної швидкості |
за часом |
t отримаємо вектор |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
P відносно ICB K , поданий через величини, що описують |
||
абсолютного прискорення a частинки |
|||||||||||||
рух частинки відносно системи K та рух самої системи K
та рух самої системи K відносно системи K :
відносно системи K :

|
|
|
|
|
|
|
|
|
|
|
|
|
|
104 |
|
d |
|
|
|
|
d |
|
|
|
|
|
d |
|
|
|
|
dV |
|
|
dr |
|
|
|
||||||
a |
|
|
|
|
|
|
|
r |
|
|
|
|
|
(4.12) |
dt |
|
dt |
|
dt |
|
dt |
|
dt |
||||||
|
|
|
|
|
|
|
||||||||
Похідна за часом t від вектора , заданого в системі K
від вектора r (див. (4.10)):
|
d |
|
|
|
|||
|
|
|
|
|
|
a |
|
|
dt |
|
|
|
|||
|
|
|
|
|
|||
|
|
d |
|
|
|||
де a |
|
|
|
– прискорення частинки P відносно HeICB |
|||
dt |
|||||||
|
|
|
|
||||
, обчислюється аналогічно похідній
(4.13)
K .
Враховуючи (4.10) та (4.13) з (4.12) можна отримати шуканий зв’язок між вектором
прискорення частинки P |
|
|
|
|
|
|
|
|
|
||||||
відносно HeICB a |
та її вектором прискорення a |
відносно ICB |
|||||||||||||
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
a |
a |
A |
|
r |
|
|
r |
2 |
|
|
, |
|
|
(4.14) |
|
dt |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dV |
|
|||
де через A позначено прискорення початку O відносно початку O , |
A |
|
. |
||||||||||||
dt |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ми бачимо, що при переході від ICB до HeICB, прискорення частинки, як і очікувалось, не |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
залишається інваріантним, а змінюється залежно від характеру руху HeICB: a |
a лише при |
||||||||||||||
0 та |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
0 , що відповідає переходу до ICB. У загальному випадку у правій частині (4.14), |
||||||||||||||
окрім a , маємо ще чотири доданки. Суму перших трьох з них називають переносним прискоренням. Переносне прискорення зумовлене виключно рухом HeICB відносно ICB і може
|
|
|
|
|
const) . Кожний із |
||
мати місце навіть для частинок, які знаходяться в спокої відносно HeICB ( r |
|
|
|||||
трьох доданків |
переносного прискорення дістав спеціальну назву. Так |
|
зване |
поступальне |
|||
|
|
|
|
|
|
|
|
прискорення |
A дорівнює прискоренню початку відліку HeICB відносно ICB, взятому зі знаком |
||||||
мінус. Його назва пов’язана з тим, що при чисто поступальному русі HeICB (коли |
0 ) лише |
||||||
|
|
|
d |
|
|
|
|
цей доданок дає внесок у переносне прискорення. Дотичне прискорення |
|
|
|
|
r |
дістало таку |
|
|
|
dt |
|||||
|
|
|
|
|
|
||
назву тому, що його вектор направлений вздовж дотичної до траєкторії частинки, яку вона описує в ICB: воно відмінне від нуля лише тоді, коли має місце прискорене обертання системи K .
Дотичне прискорення дорівнює дотичній (тангенціальній) складовій прискорення частинки при її
русі по коловій траєкторії, взятій зі знаком мінус (див. формулу (2.23а) у §2.1.5). Нарешті,
відцентрове прискорення |
|
|
|
|
|
|
r |
, яке направлене від осі обертання і дорівнює нормальній |
|

105
складовій прискорення частинки відносно ICB, взятій зі знаком мінус. Четвертий доданок
2 |
|
– це так зване коріолісове прискорення (прискорення Коріоліса). Коріолісове |
прискорення з’являється лише тоді, коли частинка рухається відносно HeICB (  0 ), яка
0 ), яка
обертається, і більше того, лише тоді, коли вектори  та не колінеарні.
та не колінеарні.
4.2. Основне рівняння динаміки частинки в HeICB
Помножимо рівність (4.14) на масу частинки m і врахуємо, що відповідно до другого закону
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ньютона перший у правій частині ma |
Fвз . Після елементарних перетворень дістанемо |
|||||||||||||
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
ma |
Fвз |
mA m |
|
|
|
r |
m |
|
|
r |
2m |
|
|
(4.15) |
|
dt |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ми отримали, таким чином, основне рівняння динаміки частинки в HeICB, яке дозволяє |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
знайти її |
прискорення |
a |
відносно |
HeICB, |
якщо |
відомі |
|
сили взаємодії Fвз , прикладені до |
||||||
частинки, а також відомий характер руху HeICB відносно довільної ICB.
Доцільно надати цьому рівнянню вигляду, подібного до рівняння другого закону Ньютона в
ICB. Тоді можна буде до задач про рух частинки відносно HeICB застосувати ті ж самі підходи,
що і в ICB. Для цього будемо записувати основне рівняння динаміки частинки в HeICB у вигляді
|
|
|
|
ma |
Fвз |
Fін |
(4.16) |
де для зручності введено так звані сили інерції Fін
|
|
d |
|
|
|
|
|
|
|
Fін |
mA m |
|
r m |
|
r 2m |
|
|
, |
(4.17) |
dt |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
пост |
|
|
|
|
|
|
|
|
|
серед яких розрізняють поступальну силу інерції |
F |
|
mA , пов’язану з поступальним |
||||||||||
|
|
|
ін |
|
|
|
|
|
|
|
|
|
|
прискоренням, відцентрову |
|
відц |
m |
|
|
|
|
|
, обумовлену |
існуванням |
|||
силу інерції F |
|
|
|
|
r |
||||||||
|
ін |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
відцентрового прискорення, |
та силу Коріоліса |
F кор |
2m |
|
|
|
. |
Сила інерції |
m |
|
r |
, |
|
|
|
|
|
||||||||||
|
|
ін |
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
зумовлена дотичним прискоренням, спеціальної назви не дістала. Відзначимо, що всі сили інерції пропорційні масі частинки, до якої вони прикладені.
Відцентрова сила інерції направлена від центру колової траєкторії, що її описує частинка
при обертанні HeICB. Якщо ввести до розгляду радіус-вектор , проведений від частинки P
106
нормально до осі обертання HeICB (Рис. 4.2), то відцентрова сила інерції може бути подана у вигляді
|
відц |
m |
2 |
|
. |
(4.18) |
F |
|
|
|
|||
ін |
|
|
|
|
|
|
Із викладеного ясно, що виникнення сил інерції пов’язане з переходом від ІСВ до HeICB: введення цих сил дозволяє зберегти зручну форму запису рівняння руху частинки: у лівій частині стоїть добуток маси частинки на її прискорення відносно HeICB, а
в правій частині — сума сил, прикладених до частинки, причому в
HeICB поряд із силами взаємодії частинки з іншими матеріальними об’єктами необхідно врахувати і сили інерції. Для сил інерції неможливо вказати джерело у вигляді певного тіла ,
що діє на частинку. Тому для сил інерції не можна вказати і сили протидії, про які йдеться в третьому законі Ньютона. Тому цей закон не застосовний до сил інерції. Це знаходиться у повній відповідності з твердженням про те, що закони динаміки Ньютона
справедливі лише в ICB.
Той факт, що сили інерції зумовлені виключно характером
руху системи відліку добре видно в демонстраційному досліді з кулькою, яка скочується по похилій площині до центру
горизонтального диску, що обертається (Рис. 4.3). Слід, що його 



 залишає на поверхні диску кулька, попередньо натерта крейдою, явно викривлений. З точки зору
залишає на поверхні диску кулька, попередньо натерта крейдою, явно викривлений. З точки зору
спостерігача, що обертається разом із диском (тобто разом з HeICB), викривлення траєкторії кульки відбувається під дією деякої сили, у даному випадку сили Коріоліса, оскільки кулька має швидкість
 . Для спостерігачів, що знаходяться в лабораторії, (тобто нерухомих відносно ICB) таке твердження виглядає дивним: вони прекрасно бачать, що відносно лабораторії (ICB) кулька рухається прямолінійно, а от поверхня диску «прокручується» під кулькою, ―утікає‖ з під неї, що й призводить до викривлення крейдяного сліду на поверхні диску.
. Для спостерігачів, що знаходяться в лабораторії, (тобто нерухомих відносно ICB) таке твердження виглядає дивним: вони прекрасно бачать, що відносно лабораторії (ICB) кулька рухається прямолінійно, а от поверхня диску «прокручується» під кулькою, ―утікає‖ з під неї, що й призводить до викривлення крейдяного сліду на поверхні диску.
Властивості сил інерції можуть бути продемонстровані в цілому ряді дослідів. Розглянемо, наприклад,
поведінку кульок, підвішених на різних відстанях від осі обертання диска, який репрезентує HeICB
(Рис.4.4), при його рівномірному обертанні. Цей дослід показує, що відхилення кульок від вертикалі зростає

107
як із збільшенням кутової швидкості обертання диску, так і при віддаленні від осі обертання (зокрема кулька, підвішена на осі обертання не відхиляється
зовсім). Розглядаючи це відхилення в HeICB, яка обертається з диском, ми інтерпретуємо його як дію
на кульку поряд із силами взаємодії — силою mg та
силою реакції нитки T — також відцентрової сили
інерції Fінвідц . Ця інтерпретація настільки наочна і
зрозуміла, що іноді складається помилкове враження про можливість пояснення ефектів такого типу лише в
HeICB.
Щоб показати цілковиту рівноправність застосування ICB та HeICB ми обговоримо цей дослід спочатку з точки зору спостерігача, що знаходиться в HeICB, тобто обертається разом з диском, а потім з
точки зору спостерігача, нерухомого відносно лабораторії,
тобто відносно поверхні Землі, яку в цьому випадку з високою точністю можна вважати за ICB.
1. Рівняння руху кульки в HeICB з початком на осі
обертання диска відповідно до Рис. 4.5 є
|
|
|
|
відц |
|
|
ma |
mg |
T |
F |
|
|
|
|
|
|
ін |
(4.19) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
де T – сила реакції підвісу, а F відц – відцентрова сила |
|
|||||
|
|
|
|
|
ін |
|
інерції. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Оскільки при рівномірному обертанні диска кулька залишається в спокої відносно диску, то a 0 , і |
||||||
|
|
|
|
|
|
|
з (4.19) маємо T |
|
mg |
Fвідц |
звідки зразу видно, що нитка відхилена від вертикалі, оскільки вектор T |
||
|
|
|
|
ін |
|
|
|
|
|
|
|
|
відц . Щоб знайти кут відхилення нитки від |
не є не колінеарний вектору g |
внаслідок появи доданку F |
|||||
|
|
|
|
|
ін |
|
вертикалі введемо для зручності декартову систему координат, жорстко зв’язану з диском, початок якої лежить на осі обертання, вісь OY якої направлена вздовж осі обертання вгору, а вісь OX — вздовж радіуса
диска в напрямку кульки (див. Рис. 4.5) і спроектуємо рівняння (4.19) на ці осі . З урахуванням умови
a 0 отримаємо:
0 |
Tx |
m |
2 |
, |
(4.20а) |
|
|||||
0 |
Ty |
mg . |
|
|
(4.20б) |

|
|
|
|
|
|
|
|
|
|
|
108 |
|
|
|
|
|
|
|
|
|
|
|
|
Таким чином, |
горизонтальна складова сили натягу T виникає внаслідок дії відцентрової сили інерції |
||||||||||
m 2 . Тангенс |
кута |
відхилення підвісу від вертикалі |
пропорційний квадрату кутової |
швидкості |
|||||||
обертання диску |
і прямо пропорційній відстані кульки від осі обертання : |
|
|
||||||||
|
T |
m |
2 |
2 |
|
|
|
|
|||
tg |
x |
|
|
|
|
|
|
. |
|
(4.21) |
|
Ty |
mg |
|
|
g |
|
||||||
|
|
|
|
|
|
|
|||||
2. При розгляді цього самого досліду в ICB необхідно врахувати лише дві сили взаємодії |
|
|
|||||||||
mg та |
T , |
||||||||||
що діють на кульку (Рис. 4.5). Відповідно, рівняння руху має вигляд |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ma |
mg |
T |
|
|
|
|
|
|
(4.22) |
||
|
|
|
|
|
|
|
|
|
|
||
На відміну від HeICB в ICB кулька не знаходиться в спокої, а рівномірно рухається по відомій |
|||||||||||
траєкторії, а саме по колу радіуса . Введемо так звану супроводжуючу систему координат |
x, y, z , яка |
||||||||||
рухається разом з кулькою. Нехай її осі OX та OZ співпадають з нормаллю та дотичною до траєкторії, а
вісь OY буде перпендикулярна до площини траєкторії і направлена вгору. Спроектуємо рівняння (4.21) на
осі OX та OY : |
|
|
||
|
|
|
|
|
|
max |
Tx , |
|
|
|
0 Ty |
mg . |
|
(4.23) |
|
|
|
|
|
|
Підставляючи в перше рівняння системи (4.23) замість ax |
величину нормальної складової прискорення |
||
2 |
отримаємо систему рівнянь для визначення кута відхилення |
, що повністю співпадає із системою |
||
|
||||
(4.20), яка має розв’язок (4.21). |
|
|
||
|
Таким чином, ми бачимо, що одна й та ж сама |
|
|
|
|
|
|
||
задача може бути однаково успішно розглянута як у |
|
A |
||
HeICB так і в ICB, але в багатьох випадках розгляд в |
|
|
||
HeICB виявляється більш наочним.
На використані сил інерції заснована дія
багатьох технічних пристроїв.
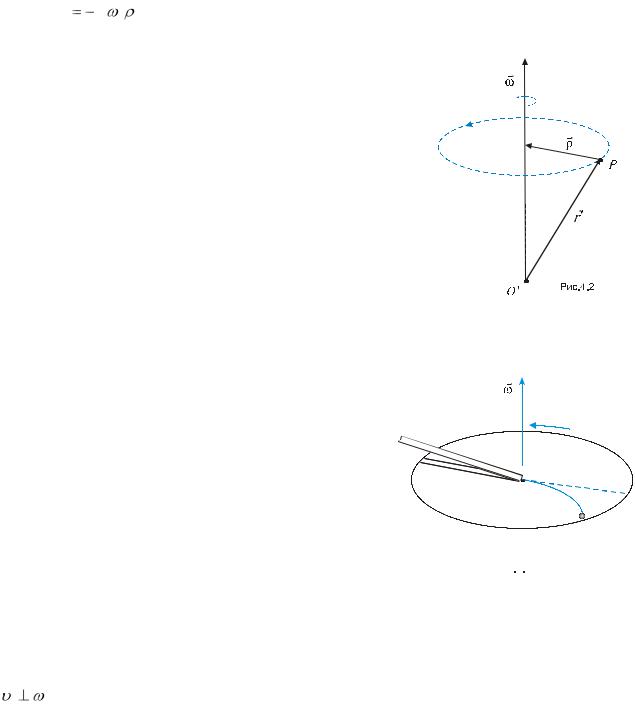
На Рис. 4.6 показано регулятор Ватта для обмеження кількості обертів у перших парових машинах.
При зростанні швидкості обертання навколо вертикальної осі два симетрично розміщені відносно осі обертання
|
|
B |
C |
|
|
|
|
|
|
|
T1 |
D |
T2 |
|
|
|
E |
|
|
|
відц |
|
М |
відц |
|
|
|||
F |
m |
|
m |
F |
1 |
|
|
|
2 |
|
|
|
|
|
|
mg |
|
mg |
|
Рис. 4.6

109
тягарці з масами m під дією відцентрової сили інерції Fінвідц віддаляються від осі обертання, що через
шарнірно з’єднані в точках А, В, С, D і E тяги до зумовлює ковзання вгору з’єднаної з ними муфти M , яка механічно сполучена з клапаном, що обмежує подачу пари.
Відцентрова сила інерції також широко використовується в різного роду насосах,
центрифугах та сепараторах, як у побуті (відцентровий водяний насос на присадибній ділянці,
центрифуга в пральній машині, сепаратор, що розділяє молоко на жир та воду), так і в найсучасніших технологіях (розділення сумішей та біологічних речовин з різною густиною в біотехнологіях, розділення ізотопів на ультрацентрифугах в ядерній фізиці, створення штучної сили тяжіння в космічних дослідженнях тощо). На наступних рисунках показано досліди, які унаочнюють принципи розділення рідин різної густини та твердих тіл різної густини занурених у рідини рідину за допомогою відцентрової сили інерції.
На Рис. 4.7 зображено скляну посудину, в яку налито ртуть, а поверх неї – воду. Коли цю посудину обертають з достатньо великою кутовою швидкістю навколо вертикальної осі, то внаслідок дії відцентрової сили інерції ртуть відкидається до найбільш віддаленої від осі ділянки стінок посудини, утворюючи дзеркальну смужку на бічній стінці посудини (Рис. 4.7а). На Рис. 4.7б показано розподіл рідин у перерізі посудини для обох випадків. Можна твердити, що цей розподіл так само як і орієнтація границь поділу
|
|
|
0 |
|
|
0 |
|
|
|||
|
|
|
|
||
|
|
|
|
|
|
|
|
вода |
|
|
вода |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
g |
|
g |
|
|
|
|
|
g |
|
|
|
ртуть |
|
|
ртуть |
Рис. 4.7
ртуть–вода та вода–повітря визначається напрямом ―сили тяжіння‖, причому у випадку нерухомої посудини
це сила тяжіння mg , яка існує біля поверхні Землі, а у випадку посудини, що обертається, роль ―сили
|
|
відц |
m |
2 |
|
. Саме за рахунок |
тяжіння‖ відіграє векторна сума сили mg та відцентрової сили інерції |
F |
|
|
|
||
|
ін |
|
|
|
|
|
обертання може бути створена штучна ―сила тяжіння‖ на космічних станціях.
110
На |
Рис. 4.8 |
наведено |
експеримент із |
|
|
|
закритою з обох кінців V-подібною трубкою, |
1 |
|
2 |
|||
|
|
|
||||
наповненою водою, |
в яку вміщено дві кульки: |
|
|
1 |
||
|
|
|
|
|
2 |
|
сталеву та коркову. У нерухомій трубці (Рис.4.8а) |
|
|
||||
|
|
|
||||
сталева кулька лежить на дні, а коркова кулька |
|
|
|
|||
такого ж розміру плаває на поверхні води в одному |
|
|
|
|||
з колін |
трубки. Якщо трубці |
надати швидкого |
|
|
Рис. 4.8 |
|
|
|
|
||||
обертання навколо вертикальної осі, то при деякій кутовій швидкості сталева та коркова кульки міняються місцями: (Рис.4.8б) коркова кулька опиняється в нижній частині трубки, разом з повітряним пухирем, а
сталева у верхній частині одного з колін!
|
ө |
|
|
|
|
|
ін |
|
|
|
|
m1 |
F1 |
m1a |
|
|
|
m1 |
Δℓ |
|
|
|
|
|
m2 F ін |
m a |
|||
|
m2 |
|
|||
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
a) |
|
|
b) |
|
Рис. 4.9 |
||||
|
|
|||
Маятник, що відхиляється на кут  від вертикалі під дією поступальної сили інерції при прискореному русі платформи, на якій його закріплено, являє собою найпростіший акселерометр – пристрій для вимірювання прискорення відносно ICB (Рис. 4.9а). Більш зручними є акселерометри, в яких про прискорення відносно ICB судять за величиною пружної деформації. Наприклад, акселерометр зображений
від вертикалі під дією поступальної сили інерції при прискореному русі платформи, на якій його закріплено, являє собою найпростіший акселерометр – пристрій для вимірювання прискорення відносно ICB (Рис. 4.9а). Більш зручними є акселерометри, в яких про прискорення відносно ICB судять за величиною пружної деформації. Наприклад, акселерометр зображений
на Рис. 4.9б складається з тягарця масою m та пружини, видовження якої l пропорційне поступальній
силі інерції, що діє на цей тягарець. Акселерометри широко застосовуються в інерціальних системах
навігації літаків, кораблів, ракет, про які йшлося в 2.1.4.
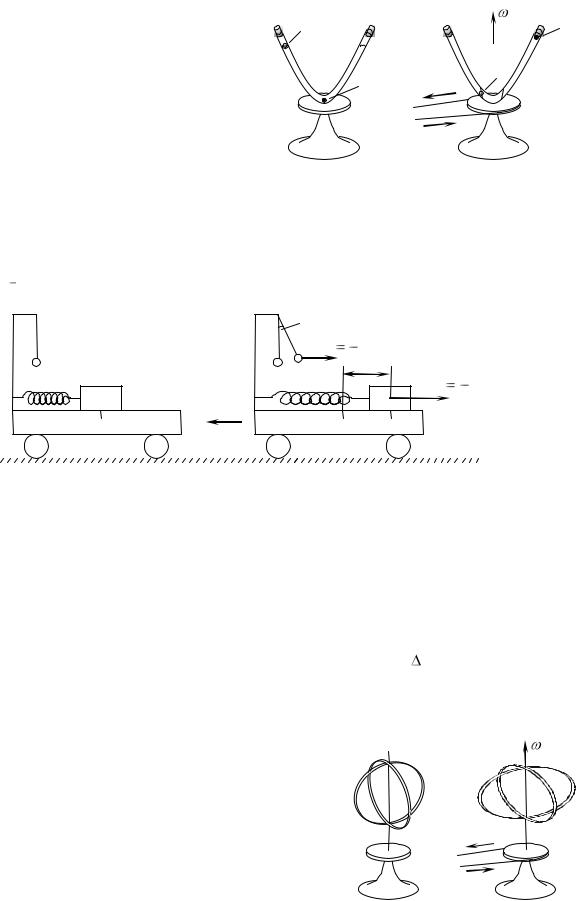
Нарешті деформація обруча при його швидкому обертанні |
|
(Рис. 4.10) демонструє руйнівну дію відцентрової сили інерції на |
|
різні маховики та ротори, а також пояснює походження фігури |
|
Землі, а саме її сплюснутість в напрямку осі обертання. (У |
|
демонстраційному пристрої муфточка M може вільно ковзати |
|
вздовж вертикальної штанги, розміщеної на осі обертання. |
Рис. 4.10 |
