15.3 Синтез контура скорости, настроенного на мо

Если требуется, что система регулирования скорости имела диапазон регулирования скорости до D_=50:1 и сравнительно невысокую точность, то целесообразно контур скорости настраивать на МО, так как в этом случае электропривод будет иметь хорошие динамические показатели качества.

В контуре скорости объектом регулирования является механическая часть электропривода, представляющая собой интергирующее звено с передаточной функцией

. (15.6)

Звеном с малой некомпенсируемой постоянной времени является контур тока, имеющий передаточную функцию второго порядка

. (15.7)

Р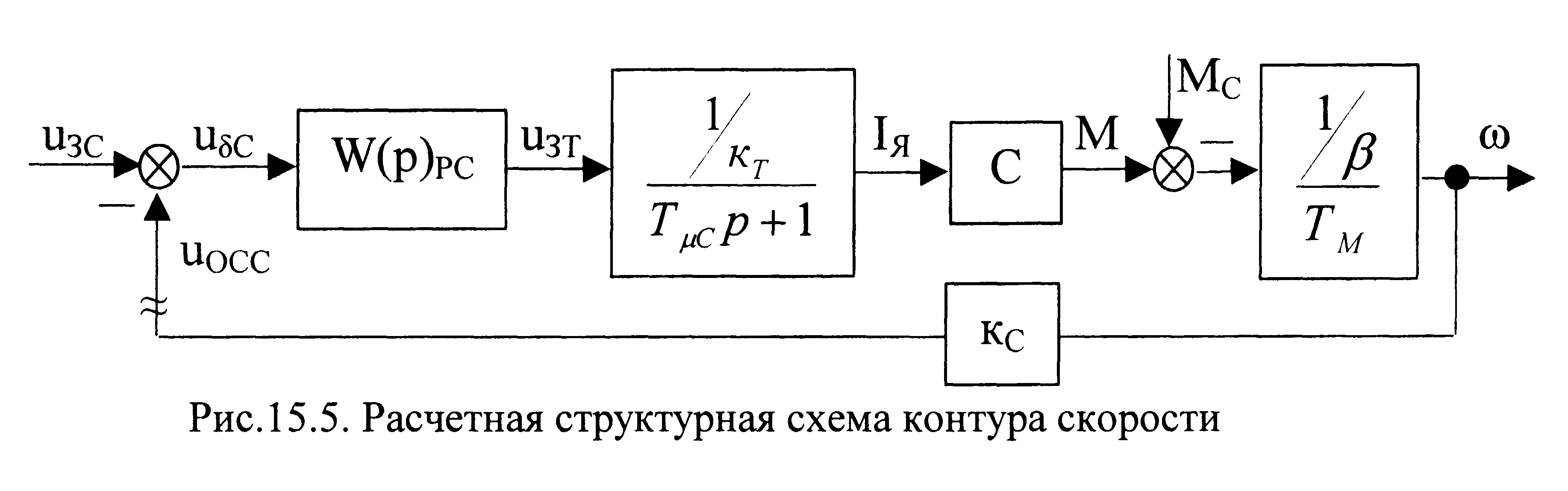асчетная структурная схема контура скорости приведена на рис.15.5. Для упрощения решения задачи синтеза контура скорости следу-ет пони-зить поря-док пере-даточной функции контура тока и счи-тать, что контур тока имеет передаточную функцию

, (15.8)

то есть Т_С=а_мТТ_Т – некомпенсируемая постоянная времени контура скорости.

При этом полная передаточная функция контура тока и упрощенная эквивалентны по времени переходного процесса t_пп.

Разомкнутый контур скорости, настроенный на МО, должен иметь передаточную функцию

,

где: а_мС=1:6 – коэффициент настройки на модульный оптимум контура скорости; а_мС=2 - стандартный коэффициент настройки на МО.

Передаточная функция регулятора скорости при настройке контура скорости на МО находится, если приравнять W(р)^р_кс =W(р)^р_{кс мо}.

.

Следовательно, регулятор скорости должен иметь передаточную функцию

. (15.9)

Таким образом, для настройки контура скорости на МО следует применять П-регулятор с коэффициентом усиления К_рс (15.9).

Передаточные функции контура скорости по задающему воздействию при настройке на МО имеют следующие выражения

, (15.10)

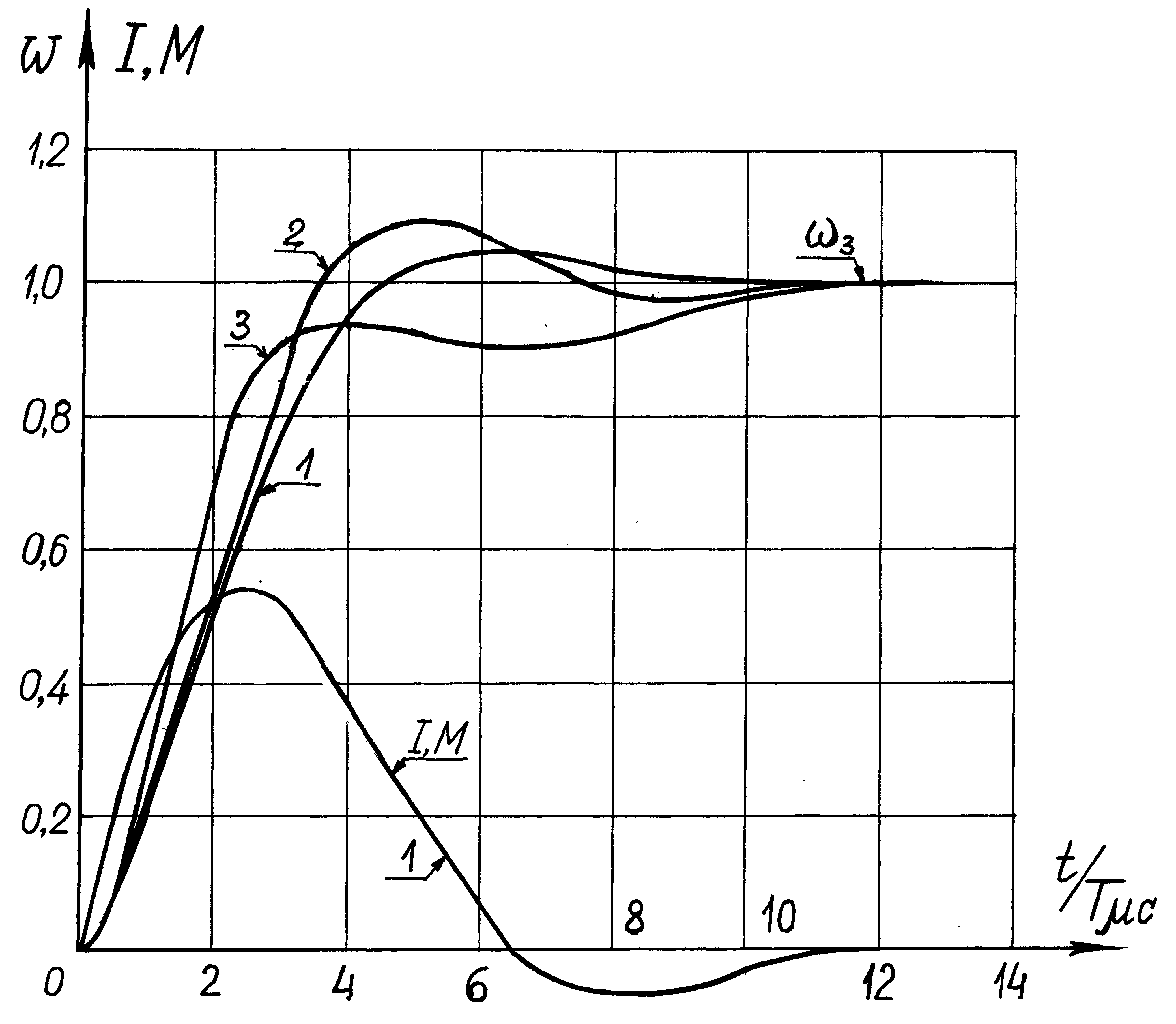где: – характеристический полином второй степени передаточной функции контура скорости, настроенного на МО,

(15.11)

.(15.12)

Передаточные функции (15.11), (15.12) отличаются только масштабными коэффициентами.

У

Рис.15.6. Переходные процессы, отработки ступенчатого задания u_ЗС при настройке контура скорости на МО

1 – малое некомпенсируемое апериодическое звено;

2 – малое некомпенсируемое высокочастотное колебательное звено

3 – с учетом э.д.с.двигателя

становившиеся значения выходных координат, I, М находятся из передаточных функций (15.10), (15.11), (15.12) при р0.

При ступенчатом сигнале u_зс-, I_уст=0, М_уст=0.

Графики переходных процессов отработки ступенчатого задания скорости приведены на рис.15.6.

Передаточная функция скорости по ошибке при отработке сигнала задания имеет вид

. (15.13)

Числитель передаточной функции по ошибке содержит сомножителем операторр в первой степени. Следовательно, контур скорости имеет астатизм первого порядка относительно сигнала задания скорости. Установившийся сигнал ошибки регулирования скорости при р0 находится из соотношения

. (15.14)

При отработке ступенчатого сигнала задания скорости установившаяся ошибка u_уст=0. Следовательно, в установившемся режиме при отработке ступенчатого сигнала задания скорости u_зC(р)=u_зC. Поэтому коэффициент обратной связи по скорости рассчитывается из соотношения

. (15.15)

где: u_зCмакс=8В – для серийных операционных усилителей с учетом возможных перерегулирований.

Передаточные функции контура скорости, по возмущению от момента сопротивления при настройке на МО имеют следующие выражения

, (15.16)

, (15.17)

. (15.18)

Передаточные функции (15.17), (15.18) отличаются только масштабом и подобны передаточным функциям по задающему воздействию .

Из передаточной функции (15.16) следует, что контур скорости при настройке но МО имеет астатизм нулевого порядка по входу М_с, и установившееся отклонение скорости от ступенчатого воздействия момента сопротивления при р0 равно

. (15.19)

Соответственно модуль жесткости механической характеристики при настройке контура скорости на МО определяется соотношением

.

Уравнение механической характеристики системы регулировани скорости при настройке контура скорости на МО

. (15.20)

Статизм по моменту сопротивления при настройке системы регулирования скорости на МО вычисляется из соотношения

,

где: – заданная скорость электропривода.

Самый большой статизм система имеет на нижней характеристике диапазона ре-гулирования. Величину этого статизма обычно указывают в технических данных системы электропривода. Поэтому с точки зрения возможного диапазона регулирования ско-рости система с настройкой на МО имеет сравнительно низкие показатели и соотве-тственно ограниченное при-менение.

Н

Рис.15.7. Переходные процессы компенсации возмущения на М_С при настройке контура скорости на МО

а рис.15.7 приведены графики переходных процессов компенсации возмущения отМ_с, когда свернутый контур тока рассматривается уп-рощенно как апериодическое звено и когда контур тока представляет собой высокочастотное колебательно звено с , то есть контур тока взят без упрощений, когда

.

Из этих графиков видно, что в реальной системе перерегулирование и время переходного процесса увеличиваются по сравнению с упрощенным вариантом. Если к тому же в расчетах учесть влияние внутренней обратной связи по э.д.с. в электродвигателе, то переходные процессы будут еще больше отличатся от идеальных, как показано на рис.15.6.