5. Эмпирическая вероятность.

Шанс случайного события мы интуитивно связываем с его частотой. Тем не менее, между этими понятиями существует принципиальное различие: шансы оцениваются заранее, до опыта, а частота может быть определена только экспериментально, после проведения серии случайных опытов в одинаковых условиях.

Далее будет введено понятие вероятности как числовой характеристики шанса, возможности появления случайного события

По частоте события мы оцениваем возможность его появления в будущем, поэтому относительную частоту называют еще эмпирической вероятностью (экспериментально вычисляемая относительная частота).

,

где Р_n(А) – эмпирическая вероятность, n – число экспериментов, А – событие,

- количество успешных экспериментов.

Основные свойства эмпирической вероятности:

• Значение вероятности находится между нулем и единицей;

• Вероятность суммы несовместных событий равна сумме их вероятностей;

• Сумма вероятностей событий, составляющих полный набор, равна единице.

6. Классическое определение вероятности

Будем предполагать, что данный эксперимент имеет N возможных исходов, все они равновозможные и несовместны, т.е. никакие два из них не могут наступить одновременно.

Вероятностью Р(А) события А называется отношение числа благоприятных исходов m(А) к общему числу N несовместных равновозможных исходов:

Р(А)=m(A)\N – классическое определение вероятности.

Выполняются три свойства:

• Для любого случайного события А .

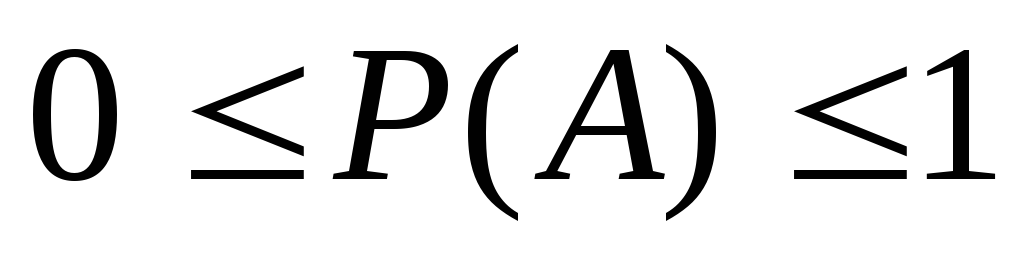• Пусть события А и В несовместны. Тогда Р(А+В)=Р(А)+Р(В).

• Пусть события 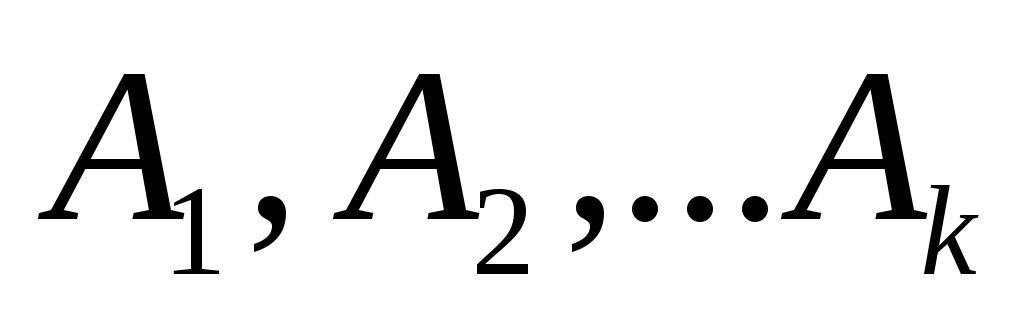образуют полный набор. Тогда

Пример 5: Рассмотрим эксперимент с бросанием монеты. У него два несовместных и равновозможных исхода: «орел» и «решка». Значит вероятность появления «орла» равна ½, вероятность появления решки равна также ½.

Пример 6: Пусть в урне находятся 2 белых и 2 чёрных шара, событие А – вынут белый шар, событие В – вынут чёрный шар. Тогда, Р(А) = ; Р(В) =. События А и В независимые, если после первого испытания шар кладётся в урну и шары перемешиваются. Если вынутый шар в первом испытании не кладётся обратно в урну, то вероятность вынуть во втором испытании шар другого цвета возрастает с до. Таким образом, событияА и В оказываются зависимыми.

Вероятность произведения двух зависимых событий А и В равна произведению вероятности одного из них на условную вероятность другого, в предположении, что первое событие уже наступило, т.е. Р(А·В) = Р(А)·Р_А(В)

Доказательство: Пусть событию А благоприятствуют m, а событию А·В – k равновозможных элементарных исходов из общего их количеств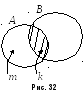аn (Рис. 32). Тогда Р(А) = ; P(А·B) = . С другой стороны, если событие А произошло, то возможны лишь те m элементарных исходов, которые благоприятствовали событию А, причём k из них благоприятствовали событию В тоже. Значит Р_А(В) = .Следовательно,

P(А·B)= =Р(А) ·Р_А(В)

Поскольку АВ = ВА имеем: Р(А·В)=Р(В·А)=Р(В)·Р_В(А)

Следствие: Для любых событий А и В справедливо равенство

Р(А)·Р_А(В) = Р(В)·Р_В(А)

Доказательство: Действительно, если А и В независимые события, то Р_А(В) = Р(В). С другой стороны, Р(А·В) = Р(А)·Р_А(В). Тогда Р(А·В) = Р(А)·Р(В).

Th: Вероятность суммы двух совместных событий А и В равна сумме вероятностей этих событий без вероятности их произведения

Р(А+В)=Р(А) + Р(В) - Р(А·В)

Доказательство:

Пусть из вcего числа n элементарных событий k благоприятствуют событию А, l – событию В, m – событиям А и В одновременно (Рис. 33). Значит событию А+В благоприятствуют k+l-m элементарных событий.

Тогда, = Р(А) + Р(В) – Р(А·В)

Задача: Два стрелка стреляют в одну и ту же цель, причём вероятность поражения цели первым стрелком 0,8, а вторым стрелком 0,5. Оба стрелка стреляют одновременно и один раз. Какова вероятность того, что цель будет поражена хотя бы одним из стрелков?

Решение: Пусть А – попадание в цель первым стрелком, В – вторым стрелком, А+В – поражение цели хотя бы одним стрелком, А·В – поражение цели обоими стрелками. Тогда Р(А+В)=0,8 + 0,5 – Р(А·В). Считая события А и В независимыми имеем: Р(А·В) = Р(А)·Р(В) = 0,8·0,5 = 0,4

Ответ: Р(А+В) = 0,9

Задача: В ящике имеются 7 белых и 5 чёрных шаров, отличающихся лишь цветом. Опыт состоит в том, что сначала вынимают (не глядя) один шар и, не опуская его обратно, вынимают ещё один шар. Какова вероятность, что оба вынутых шара чёрные?

Решение: Появление первого чёрного шара (событие А) имеет вероятность . Если первый шар оказался чёрным, то условная вероятность события В – появление второго чёрного шара (при условии, что первый шар был чёрным) – равна Р_А(В)=, т.к. перед выниманием второго шара осталось 11 шаров, из них 4 чёрных. Вероятность вынуть два чёрных шара подряд можно подсчитать по формуле:

P(А·B) = Р(А) ·Р_А(В)

Th.(формула полной вероятности) Вероятность события А, которое может наступить лишь при условии появления одного из n попарно несовместимых событий В₁, В₂, В₃, … , B_n, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А, т.е.

Р(А)=Р(В₁)·(А) + Р(В₂)·(А) + … + Р(В_n)·(A)

Доказательство: Событие А может наступить лишь при условии наступления одного из событий В₁, В₂, В₃, … , B_n, т.е. В₁А + В₂А + В₃А + … + B_nА, причём события В₁А , В₂А , В₃А , … , B_nА несовместимы, т.к. несовместимы события В₁, В₂, В₃, … , B_n. Тогда на основании теорем сложения и умножения вероятностей имеем Р(А)=Р(В₁А) + Р(В₂А) + Р(В₃А) + … + Р(B_nА) = Р(В₁)·(А) + +Р(В₂)·(А) + … + Р(В_n)·(A) или

При условиях формулы полной вероятности справедлива формула Байеса:

, где k=1, 2, …, n

Задача: Для приёма зачёта преподаватель заготовил 50 задач: 20 задач по дифференциальному исчислению, 30 – по интегральному исчислению. Для получения зачёта студент должен решить первую же достающуюся наугад задачу. Какова вероятность для студента сдать зачёт, если он умеет решать 18 задач по дифференциальному исчислению и 15 задач по интегральному исчислению.

Решение: Вероятность получить задачу по дифференциальному исчислению (событие В₁) равна Р(В₁)=0,4, по интегральному исчислению (событие В₂) – Р(В₂)=0,6. Если событие А означает, что задача решена, то (А)=0,9,(А)=0,5. Тогда Р(А)=0,4·0,9 + 0,6·0,5 = 0,36 + 0,3 = 0,66