29. Проблема разрешимости (разрешения) для класса однотипных задач. Проблема разрешимости в алгебре высказываний и способы их разрешения.

Проблема разрешимости для класса однотипных задач. Проблема разрешимости в алгебре высказываний и способы их разрешения.

Все формулы алгебры логики делятся на три класса: тавтологии (тождественно истинные),тождественно ложные, выполнимые.

Формулу А называют тождественно истинной, если она при всех значениях входящих в неё переменных высказываний принимает значение 1(истина). Формулу А называют тождественно ложной, если она при всех значениях входящих в неё переменных принимает значение 0(ложь).Формулу A называют выполнимой, если она принимает значение 1(истина), хотя бы на одном наборе входящих в нее переменных и не является тождественно истинной.

Вопрос к какому классу формул относится текущая формула A и называется проблемой разрешимости.  Эта проблема решается элементарно с помощью таблицы истинности, однако для больших формул таблицы очень громоздки и их использование затруднительно.

Другой способ основан на приведение формулы A к КНФ (конъюнктивная нормальная формула) или ДНФ (дизъюнктивная) и использовании специального алгоритма, который позволяет определить является ли данная формула тождественно истинной или не является. Одновременно с этим решается проблема разрешимости.

Механизм применения вышеназванного алгоритма таков. Сначала он применяется к формуле A. Если A1 то задача решена. Если это не так, то алгоритм применяется к формуле ¬A Если ¬A 1  то A0 и задача решена. Если это не так, то A - выполнимая формула.

Механизм установления тождественной истинности формулы A основан на следующих теоремах.

     Теорема 3. Для того, чтобы элементарная дизъюнкция (сумма переменных и их отрицаний) была тождественно истинной, необходимо и достаточно, чтобы в ней содержалась переменная и ее отрицание ( x_i v ¬x_i1)

     Теорема 4. Для того, чтобы элементарная конъюнкция (произведение переменных и их отрицаний) была тождественно ложной, необходимо и достаточно, чтобы в ней содержалась переменная и ее отрицание.

( x_i ^ ¬x_i0) 

     Теорема 5. Для того, чтобы формула алгебры логики A была тождественно истинна, необходимо и достаточно, чтобы каждая элементарная дизъюнкция, входящая в КНФ (конъюктивная нормальная форма – произведение элементарных сумм (дизъюнкций)) A, содержала переменную и ее отрицание. Доказательство:

Необходимо. Пусть  A1  Тогда КНФ A1  и КНФAA₁ ^A₂ ^A₃ ^...^A_n ^1 -> 

^V₁=¬(1,n), A_i1

Так как  A_i - элементарная дизъюнкция, то по теореме 3  A_i  содержит переменную и ее отрицание.

Достаточно. Пусть  A_i - содержит переменную и ее отрицание. Тогда по теореме 3  A_i1, i=¬(1,n)  Но  Следовательно A- тождественно истинная формула.

Теорема 6. Для того, чтобы формула алгебры логики A была тождественно ложной, необходимо и достаточно, чтобы каждая элементарная конъюнкция, входящая в ДНФ (дизъюнктивная нормальная форма сумма элементарных произведений (конъюнкций)) A, содержала переменную и ее отрицание.

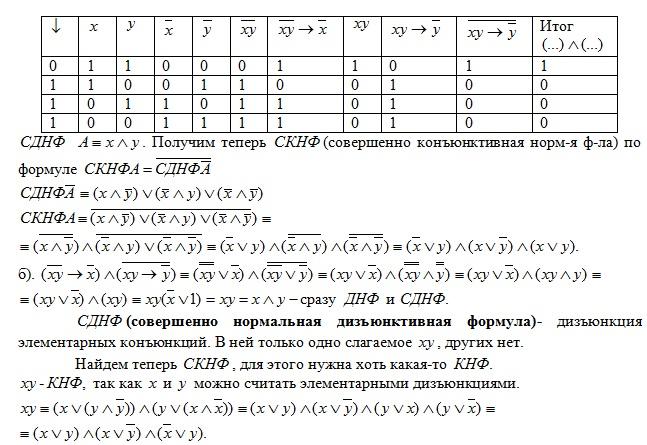
Примеры. A=(¬(xy) -> ¬x) ^ ¬(xy -> ¬y) Получить  СДНФ  и СКНФ с помощью таблицы истинности и путем элементарных преобразований.

а).   с помощью таблицы истинности  

45. Моделирование как метод познания. Понятие «модель». Варианты представления моделей. Натурные и абстрактные модели. Виды моделирования в естественных и технических науках. Компьютерная модель. Абстрактные модели и их классификация. Вербальные модели.

Компьютерное моделирование как метод научного познания

Курс Компьютерное моделирование - это новый и довольно сложный курс в цикле информационных дисциплин. Постольку, поскольку курс КМ является междисциплинарным курсом для его успешного освоения требуется наличие самых разнообразных знаний: во-первых, знаний в выбранной предметной области - если мы моделируем физические процессы, мы должны обладать определенным уровнем знания законов физики, моделируя экологические процессы - биологических законов, моделируя экономические процессы - знанием законов экономики, кроме того, т.к. компьютерное моделирование использует практически весь аппарат современной математики, предполагается знание основных математических дисциплин - алгебры, матанализа, теории дифференциальных уравнений, матстатистики, теории вероятности. Для решения математических задач на компьютере необходимо владеть в полном объеме численными методами решения нелинейных уравнений, систем линейных уравнений, дифференциальных уравнений, уметь аппроксимировать и интерполировать функции. И, конечно же, предполагается свободное владение современными информационными технологиями, знание языков программирования и владение навыками разработки прикладных программ.

Компьютерное моделирование, возникшее как одно из направлений математического моделирования с развитием информационных компьютерных технологий стало самостоятельной и важной областью применения компьютеров. В настоящее время компьютерное моделирование в научных и практических исследованиях является одним из основных методов познания. Без компьютерного моделирования сейчас невозможно решение крупных научных и экономических задач. Выработана технология исследования сложных проблем, основанная на построении и анализе с помощью вычислительной техники математической модели изучаемого объекта. Такой метод исследования называется вычислительным экспериментом. Вычислительный эксперимент применяется практически во всех отраслях науки - в физике, химии, астрономии, биологии, экологии, даже в таких сугубо гуманитарных науках как психология, лингвистика и филология, кроме научных областей вычислительные эксперименты широко применяются в экономике, в социологии, в промышленности, в управлении. Проведение вычислительного эксперимента имеет ряд преимуществ перед так называемым натурным экспериментом:

• для ВЭ не требуется сложного лабораторного оборудования;

• существенное сокращение временных затрат на эксперимент;

• возможность свободного управления параметрами, произвольного их изменения, вплоть до придания им нереальных, неправдоподобных значений;

• возможность проведения вычислительного эксперимента там, где натурный эксперимент невозможен из-за удаленности исследуемого явления в пространстве (астрономия) либо из-за его значительной растянутости во времени (биология), либо из-за возможности внесения необратимых изменений в изучаемый процесс.

В этих случаях и используется КМ. Также широко используется КМ в образовательных и учебных целях. КМ - наиболее адекватный подход при изучении предметов естественнонаучного цикла, изучение КМ открывает широкие возможности для осознания связи информатики с математикой и другими науками - естественными и социальными. Учитель может использовать на уроке готовые компьютерные модели для демонстрации изучаемого явления, будь это движение астрономических объектов или движение атомов или модель молекулы или рост микробов и т.д., также учитель может озадачить учеников разработкой конкретных моделей, моделируя конкретное явление ученик не только освоит конкретный учебный материал, но и приобретет умение ставить проблемы и задачи, прогнозировать результаты исследования, проводить разумные оценки, выделять главные и второстепенные факторы для построения моделей, выбирать аналогии и математические формулировки, использовать компьютер для решения задач, проводить анализ вычислительных экспериментов. Таким образом, применение КМ в образовании позволяет сблизить методологию учебной деятельности с методологией научно-исследовательской работы, что должно быть интересно вам, как будущим педагогам.

Понятие моделирования - это очень широкое понятие, оно не ограничивается только математическим моделированием. Истоки моделирования обнаруживаются в далеком прошлом. Наскальные изображения мамонта, пронзенного копьем, на стене пещеры можно рассматривать как модель удачной охоты, созданную древним художником.

Элементы моделирования часто присутствуют в детских играх, любимое занятие детей - моделировать подручными средствами предметы и отношения из жизни взрослых. Взрослеют дети, взрослеет человечество. Человечество познает окружающий мир, модели становятся более абстрактными, теряют внешнее сходство с реальными объектами. В моделях отражаются глубинные закономерности, установленные в результате целенаправленных исследований. В роли моделей могут выступать самые разнообразные объекты: изображения, схемы, карты, графики, компьютерные программы, математические формулы и т.д. Если мы заменяем реальный объект математическими формулами (допустим, согласно 2 закону Ньютона, опишем движение некоторого тела системой нелинейных уравнений, или, согласно закону теплопроводности опишем процесс распространения тепла дифференциальным уравнение 2 порядка), то говорят о математическом моделировании, если реальный объект заменяем компьютерной программой - о компьютерном моделировании.

Но что бы ни выступало в роли модели, постоянно прослеживается процесс замещения реального объекта с помощью объекта-модели с целью изучения реального объекта или передачи информации о свойствах реального объекта. Это процесс и называется моделированием. Замещаемый объект называется оригиналом, замещающий - моделью.

Классификация моделей

В зависимости от средств построения различают следующие классы моделей:

• словесные или описательные модели их также в некоторой литературе называют вербальными или текстовыми моделями (например, милицейский протокол с места проишествия, стихотворение Лермонтова "Тиха украинская ночь");

• натурные модели (макет Солнечной системы, игрушечный кораблик);

• абстрактные или знаковые модели. Интересующие нас математические модели явлений и компьютерные модели относятся как раз к этому классу.

Можно классифицировать модели по предметной области:

• физические модели,

• биологические,

• социологические,

• экономические и т.д.

Классификация модели по применяемому математическому аппарату:

• модели, основанные на применении обыкновенных дифференциальных уравнений;

• модели, основанные на применении уравнений в частных производных;

• вероятностные модели и т.д.

Также можно классифицировать модели по цели моделирования. В зависимости от целей моделирования различают:

• Дескриптивные модели (описательные) описывают моделируемые объекты и явления и как бы фиксируют сведения человека о них. Примером может служить модель Солнечной системы, или модель движения кометы, в которой мы моделируем траекторию ее полета, расстояние, на котором она пройдет от Земли У нас нет никаких возможностей повлиять на движение кометы или движение планет Солнечной системы;

• Оптимизационные модели служат для поиска наилучших решений при соблюдении определенных условий и ограничений. В этом случае в модель входит один или несколько параметров, доступных нашему влиянию, например, известная задача коммивояжера, оптимизируя его маршрут, мы снижаем стоимость перевозок. Часто приходится оптимизировать процесс по нескольким параметрам сразу, причем цели могут быть весьма противоречивы, например, головная боль любой хозяйки - как вкуснее, калорийнее и дешевле накормить семью;

• Игровые модели (компьютерные игры);

• Обучающие модели (всевозможные тренажеры);

• Имитационные модели (модели, в которых сделана попытка более или менее полного и достоверного воспроизведения некоторого реального процесса, например, моделирование движения молекул в газе, поведение колонии микробов и т.д.).

Существует также классификация моделей в зависимости от их изменения во времени. Различают

• Статические модели - неизменные во времени;

• Динамические модели - состояние которых меняется со временем.

Основные понятия

В технологии компьютерного моделирования можно выделить следующие основные понятия.

Модель - искусственно созданный объект, который воспроизводит в определенном виде реальный объект - оригинал.

Компьютерная модель - представление информации о моделируемой системе средствами компьютера.

Система - совокупность взаимосвязанных элементов, обладающих свойствами, отличными от свойств отдельных элементов.

Элемент - это объект, обладающий свойствами, важными для целей моделирования. В компьютерной модели свойства элемента представляются величинами - характеристиками элемента.

Связь между элементами описывается с помощью величин и алгоритмов, в частности вычислительных формул.

Состояние системы представляется в компьютерной модели набором характеристик элементов и связей между элементами. Структура данных, описывающих состояние, не зависит от конкретного состояния и не меняется при смене состояний, меняется только значение характеристик.

Если состояния системы функционально зависят от некоторого параметра, то процессом называют набор состояний, соответствующий упорядоченному изменению параметра. Параметры в системе могут меняться как непрерывно, так и дискретно. В компьютерной модели изменение параметра всегда дискретно. Непрерывные процессы можно моделировать на компьютере, выбирая дискретную серию значений параметра так, чтобы последовательные состояния мало чем отличались друг от друга, или, другими словами, минимизируя шаг по времени.

В свете введенных определений можно дать более строгие определения некоторым классам моделей.

Статистические модели - модели, в которых предоставлена информация об одном состоянии системы.

Динамические модели - модели, в которых предоставлена информация о состояниях системы и процессах смены состояний. Оптимизационные, имитационные и вероятностные модели являются динамическими моделями.

В оптимизационных и имитационных моделях последовательность смены состояний соответствует изменению моделируемой системы во времени. В вероятностных моделях смена состояний определяется случайными величинами.

В технологии КМ можно выделить несколько этапов.

Этапы компьютерного моделирования

Этапы КМ можно представить в виде схемы

Объект изучения	→	Формальная модель	→	Программирование модели
				↓
Информационная модель	←	Компьютерный эксперимент	←	Отладка/тестирование

Моделирование начинается с объекта изучения. На 1 этапе формируются законы, управляющие исследованием, происходит отделение информации от реального объекта, формируется существенная информация, отбрасывается несущественная, происходит первый шаг абстракции. Преобразование информации определяется решаемой задачей. Информация, существенная для одной задачи, может оказаться несущественной для другой. Потеря существенной информации приводит к неверному решению или не позволяет вообще получить решение. Учет несущественной информации вызывает излишние сложности, а иногда создает непреодолимые препятствия на пути к решению. Переход от реального объекта к информации о нем осмыслен только тогда, когда поставлена задача. В тоже время постановка задачи уточняется по мере изучения объекта. Т.о. на 1 этапе параллельно идут процессы целенаправленного изучения объекта и уточнения задачи. Также на этом этапе информация об объекте подготавливается к обработке на компьютере. Строится так называемая формальная модельявления, которая содержит:

• Набор постоянных величин, констант, которые характеризуют моделируемый объект в целом и его составные части; называемых статистическим или постоянными параметрами модели;

• Набор переменных величин, меняя значение которых можно управлять поведением модели, называемых динамическим или управляющими параметрами;

• Формулы и алгоритмы, связывающие величины в каждом из состояний моделируемого объекта;

• Формулы и алгоритмы, описывающие процесс смены состояний моделируемого объекта.

На 2 этапе формальная модель реализуется на компьютере, выбираются подходящие программные средства для этого, строиться алгоритм решения проблемы, пишется программа, реализующая этот алгоритм, затем написанная программа отлаживается и тестируется на специально подготовленных тестовых моделях. Тестирование - это процесс исполнения программы с целью выявления ошибок. Подбор тестовой модели - это своего рода искусство, хотя для этого разработаны и успешно применяются некоторые основные принципы тестирования. Тестирование - это процесс деструктивный, поэтому считается, что тест удачный, если обнаружена ошибка. Проверить компьютерную модель на соответствие оригиналу, проверить насколько хорошо или плохо отражает модель основные свойства объекта, часто удается с помощью простых модельных примеров, когда результат моделирования известен заранее.

На 3 этапе, работая с компьютерной моделью мы осуществляем непосредственно вычислительный эксперимент. Исследуем, как поведет себя наша модель в том или ином случае, при тех или иных наборах динамических параметров, пытаемся прогнозировать или оптимизировать что-либо в зависимости от поставленной задачи.

Результатом компьютерного эксперимента будет являться информационная модель явления, в виде графиков, зависимостей одних параметров от других, диаграмм, таблиц, демонстрации явления в реальном или виртуальном времени и т.п.

46.      Информационные модели. Объекты и их связи. Основные структуры в информационном моделировании. Примеры информационных моделей. Объектно-ориентированное программирование. Свойства ООП: инкапсуляция, наследование и полиморфизм. Класс и объектный тип. Структура класса, поля, методы и свойства. Абстрактные, виртуальные, динамические и перегружаемые методы.

ИНФОРМАЦИОННЫЕ МОДЕЛИ представляют объекты или процессы в образной или знаковой форме. Рисунки, фотографии, учебные плакаты – это  образные информационные модели. Примеры знаковых информационных моделей:  программа на языке программирования, формулы законов физики, химии, биологии,  периодическая таблица химических элементов, географическая карта.

Информационные модели (знаковые): описательная, табличная, математическая (интегральная, дифференциальная, имитационная, дискретная и др.).

Информационные модели (знаковые) по структуре организации данных: иерархическая, сетевая, табличная, линейная.

Описательная информационная модель – совокупность данных, содержащих текстовую информацию об объекте-оригинале. Для создания описательных информационных моделей используются естественные языки.

Табличная информационная модель – таблица, содержащая информацию об объекте-оригинале. Например, таблица, содержащая информацию о планетах Солнечной системы (расстояние, размеры, температуру, период обращения вокруг Солнца).

Математическая информационная модель – математические формулы, описывающие форму или поведение объекта-оригинала.

В том числе имитационная (математическая) модель. При имитационном моделировании воспроизводится алгоритм функционирования системы во времени – поведение системы; причем имитируются элементарные явления, составляющие процесс, с сохранением их логической структуры и последовательности протекания, что позволяет по исходным данным получить сведения о состояниях процесса в определенные моменты времени, дающие возможность оценить характеристики системы. Основным преимуществом имитационного моделирования является возможность решения сложных задач. Имитационные модели позволяют достаточно просто учитывать такие факторы, как наличие дискретных и непрерывных элементов, нелинейные характеристики элементов системы, многочисленные случайные воздействия и другие, которые часто создают трудности при аналитических исследованиях. В настоящее время имитационное моделирование – наиболее эффективный метод исследования систем, а часто и единственный практически доступный метод получения информации о поведении системы.

 

По структуре организации данных информационные модели могут быть иерархические, сетевые, модели линейной структуры, табличные.

Иерархическая информационная модель имеет упорядоченную структуру, где объект нижнего уровня связан только с одним объектом предыдущего уровня, но любой объект вышестоящего уровня может быть связан с несколькими объектами последующего уровня.

Современная классификация представителей животного мира  является иерархической информационной моделью.

Табличная информационная модель – таблица, содержащая информацию об объекте-оригинале. Например, таблица, содержащая информацию о планетах Солнечной системы (расстояние, размеры, температуру, период обращения вокруг Солнца).

В сетевой модели объекты не упорядочены по уровням. Вспомните сетевую модель баз данных.

В линейной структуре объекты соединены в одну цепь.

Существует три вида  связи :

• один-к-одному (рис. 1),

• один-ко-многим (рис. 2) и

• многие-ко-многим (рис. 3).

     Связь  один-к-одному существует, когда один экземпляр одного  объекта  связан с единственным экземпляром другого.  Связь  один-к-одному обозначается стрелкой:

Рис.1.  Связь  один-к-одному

     Связь  один-ко-многим существует, когда один экземпляр первого  объекта  связан с одним или более экземпляром второго  объекта , но каждый экземпляр второго связан только с одним экземпляром первого. Множественность  связи изображается двойной стрелкой:

Рис.2.  Связь  один-ко-многим

     Связь  многие-ко-многим существует, когда один экземпляр первого  объекта  связан с одним или большим количеством экземпляров второго и каждый экземпляр второго  объекта  связан с одним или многими экземплярами первого:

Рис.3.  Связь  многие-ко-многим

    Помимо множественности,  связи  могут подразделяться на безусловные и условные. В безусловной  связи  для участия в ней требуется каждый экземпляр  объекта . В условной  связи  принимают участие не все экземпляры объекта .  Связь  может быть условной как с одной, так и с обеих сторон

Пример информационной модели

Представьте себе, что нужно отгадать загадку. Вам предлагают перечень свойств реального предмета: круглое, зеле­ное, глянцевое, прохладное, полосатое, звонкое, зрелое, ароматное, сладкое, сочное, тяжелое, крупное, с сухим хвостиком...

Список можно продолжать, но вы, наверное, уже догадались, что речь идет об арбузе. Информация о нем дана самая разнообразная: и цвет, и запах, и вкус, и даже звук... Очевидно, ее гораздо больше, чем требуется для решения этой задачи. Попробуйте выбрать из всех пере­численных признаков и свойств минимум, по­зволяющий безошибочно определить объект. В русском фольклоре давно найдено решение: «Сам алый, сахарный, кафтан зеленый, бархат­ный».

Если бы информация предназначалась художнику для написания натюрморта, можно было ограничиться следующими свойствами объек­та: круглый, большой, зеленый, полосатый. Чтобы вызвать аппетит у сладкоежки выбрали бы другие свойства: зрелый, сочный, ароматный, сладкий. Для человека, выбирающего арбуз на бахче, можно предложить- крупный, звонкий, с сухим хвостиком.

 

Объектно-ориентированное программирование

ООП возникло в результате развития идеологии процедурного программирования, где данные и подпрограммы (процедуры, функции) их обработки формально не связаны. Для дальнейшего развития объектно-ориентированного программирования часто большое значение имеют понятия события (так называемое событийно-ориентированное программирование) и компонента (компонентное программирование, КОП).

Формирование КОП от ООП произошло, как случилось формирование модульного от процедурного программирования: процедуры сформировались в модули — независимые части кода до уровня сборки программы, так объекты сформировались в компоненты — независимые части кода до уровня выполнения программы. Взаимодействие объектов происходит посредством сообщений. Результатом дальнейшего развития ООП, по-видимому, будет агентно-ориентированое программирование, где агенты — независимые части кода на уровне выполнения. Взаимодействие агентов происходит посредством изменения среды, в которой они находятся.

Языковые конструкции, конструктивно не относящиеся непосредственно к объектам, но сопутствующие им для их безопасной (исключительные ситуации, проверки) и эффективной работы, инкапсулируются от них в аспекты (в аспектно-ориентированном программировании). Субъектно-ориентированное программирование расширяет понятие объект посредством обеспечения более унифицированного и независимого взаимодействия объектов. Может являться переходной стадией между ООП и агентным программирование в части самостоятельного их взаимодействия.

Первым языком программирования, в котором были предложены принципы объектной ориентированности, была Симула. В момент своего появления (в 1967 году), этот язык программирования предложил поистине революционные идеи: объекты, классы, виртуальные методы и др., однако это всё не было воспринято современниками как нечто грандиозное. Именно он стал первым широко распространённым объектно-ориентированным языком программирования.

Инкапсуляция 

Инкапсуляция — это свойство системы, позволяющее объединить данные и методы, работающие с ними, в классе и скрыть детали реализации от пользователя.

Наследование 

Наследование — это свойство системы, позволяющее описать новый класс на основе уже существующего с частично или полностью заимствующейся функциональностью. Класс, от которого производится наследование, называется базовым, родительским или суперклассом. Новый класс — потомком, наследником или производным классом.

Полиморфизм 

Полиморфизм — это свойство системы использовать объекты с одинаковым интерфейсом без информации о типе и внутренней структуре объекта.

Класс и объектный тип

Базовыми блоками объектно-ориентированной програм­мы являются объекты и классы. Содержательно объект мож­но представить как что-то ощущаемое или воображаемое и имеющее хорошо определенное поведение. Таким образом, объект можно либо увидеть, либо потрогать, либо, по край­ней мере, знать, что он есть, например, представлен в виде информации, хранимой в памяти компьютера. Дадим определение объекта, придерживаясь мнения Гради Буча: «Объект – осязаемая сущность, которая четко проявляет свое поведение».

Объект — это часть окружающей нас реальности, т. е. он существует во времени и в пространстве (впервые понятие объекта в про­граммировании введено в языке Simula ). Формально объект определить довольно трудно. Это можно сделать че­рез некоторые свойства, а именно: объект имеет состояние, поведение и может быть однозначно идентифицирован (дру­гими словами, имеет уникальное имя).

Класс — это множество объектов, имеющих общую структуру и общее поведение. Класс — описание (абстракция), которое показывает, как построить существующую во време­ни и пространстве переменную этого класса, называемую объектом.Смысл предложений «описание переменных клас­са» и «описание объектов класса» один и тот же.

Объект имеет состояние, поведение и паспорт (средство для его однозначной идентификации); структура и поведение объектов описаны в классах, переменными которых они яв­ляются .

Структура класса

По своей природе, класс – это генеральный контракт между абстракцией и всеми ее клиентами. Выражением обязательства класса служит его интерфейс. Класс задается своим типом (именем класса), информацией о суперклассах и реализуемых интерфейсах, а также своими членами (полями, методами и внутренними абстракциями). Члены класса могут реализовывать свойства объекта (поля и методы экземпляра), а могут реализовывать свойства собственного класса (статические поля и методы). Для поддержки принципа инкапсуляции, существует четыре основных уровня доступа к членам класса:

o                Открытый (public) доступ – члены класса видимы всем клиентам класса;

o                Защищенный (protected) – члены этого уровня видимы самому классу, его подклассам и абстракциям, находящимся с ним в одном пакете.

o                Пакетный (в java) – члены этого уровня доступны только самому классу и абстракциям, находящимися с ним в одном пакете.

o                Закрытый (private) – члены этого уровня видимы только изнутри самого класса.

 

Абстрактные методы и классы

Свойство: При построении сложной иерархии, для обеспечения полиморфизма программисты часто вынуждены вводить методы в классы верхнего уровня, даже если эти методы ещё не определены для этой специфической абстракции. Здесь можно было бы оставить пустые методы, но многие ОО языки предлагают такой специфический механизм, как определение абстрактных методов, то есть методов без реализации. Классы, имеющие хотя бы один абстрактный метод, часто называются абстрактными классами.

C++: В C++ абстрактные методы или чисто виртуальные функции получаются добавлением так называемого чистого описателя (=0) в определение метода. Абстрактные классы являются просто классами с одним или более абстрактным методом (или наследующие их). Вы не можете создать объект абстрактного класса.

OP: Object Pascal для выделения этих методов использует ключевое слово abstract. Кроме того, абстрактными классами являются классы, имеющие или наследующие абстрактные методы. Вы можете создать объект абстрактного класса (хотя компилятор выдаст предупреждающее сообщение). Это подвергает программу риску вызвать абстрактный метод, что приведёт к генерации ошибки времени выполнения и завершению программы.

Виртуальные методы

Наследование позволяет создавать иерархические, связанные отношениями подчинения, структуры данных. Следует, однако, заметить, что при использовании этой возможности могут возникнуть проблемы. Предположим, что в нашей графической программе необходимо определить объект Circle, который является потомком другого объекта Point:

Type

Circle = object (point)

Radius: Integer;

Procedure Show;

Procedure Hide;

Procedure Expand(ExpandBy: Integer);

Procedure Contact(ContactBy: Integer);

End;

Новый объект Circle соответствует окружности. Поскольку свойства окружности отличаются от свойств точки, в объекте-наследнике придется изменять процедуры Show и Hide, которые отображают окружность и удаляют её изображение с экрана. Может оказаться, что метод Init (см. предыдущий пример) объекта Circle, унаследованный от объекта Point, также использует методы Show и Hide, впредь во время трансляции объекта Point использует ссылки на старые методы. Очевидно в объекте Circle они работать не будут.

Можно, конечно, попытаться «перекрыть» метод Init. Чтобы это сделать, нам придётся полностью воспроизвести текст метода. Это усложни работу, да и не всегда возможно, поскольку исходного текста программы может не оказаться под рукой (если объект-родитель уже находиться в оттранслированном модуле).

Для решения этой проблемы используется виртуальный метод. Связь между виртуальным методом и вызывающими их процедурами устанавливается не во время трансляции (это называется ранним связанием), а во время выполнения программы (позднее связание.

Чтобы использовать виртуальный метод, необходимо в описании объекта после заголовка метода добавить ключевое слово virtual. Заголовки виртуальных методов родителя и наследника должны в точности совпадать.

 

Динамическое создание объектов

Переменные объектного типа могут быть динамическими, то есть размещаться в памяти только во время их использования. Для работы с динамическими объектами используются расширенный синтаксис процедур New и Dispose. Обе процедуры в этом случае содержат в качестве второго параметра вызов конструктора или деструктора для выделения или освобождения памяти переменной объектного типа:

New(P, Construct) или

Dispose(P, Destruct)

Где P - указатель на переменную объектного типа, а Construct или Destruct - конструктор и деструктор этого типа.

Действие процедуры New в случае расширенного синтаксиса равносильно действию следующей пары операторов:

New(P);

P^.Construct;

Эквивалентом Dispose является следующее:

Перегруженные методы

В процедурном программировании тоже существует понятие полиморфизма, которое отличается от рассмотренного механизма в  ООП . Процедурный полиморфизм предполагает возможность создания нескольких процедур или функций с одним и тем же именем, но разным количеством или различными типами передаваемых параметров. Такие одноименные функции называются  перегруженными , а само явление - перегрузкой (overloading). Перегрузка функций существует и в  ООП  и называется перегрузкой  методов