Численные методы

1. Метод простой итерации при решении уравнения с одной переменной.

2. Метод простой итерации для СЛАУ.

3. Интерполяционный многочлен Лагранжа. Вывод, оценка погрешности.

4. Метод трапеций для численного нахождения определенного интеграла: вывод формулы, оценка погрешности, геометрический смысл.

5. Методы численного интегрирования дифференциальных уравнений.

6. Метод наименьших квадратов.

1. Метод простой итерации при решении уравнения с одной переменной.

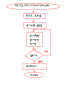
Дано F(x)=0 (1)

Заменим уравнение F( x ) = 0 равносильным уравнением X =f(x) (2)

Пусть на [a,b] содерж единств корень ур-я (2).

Выберем из интервала [a,b] произвольное число x₀ и подставим в правую часть (2). Получим число x₁: x₁=f(x₀)

Подставляем х₁ в правую часть (2) получим х₂ и т.д.

x_k = f(x_k-1) (3)

Последовательность х₀, x₁, …, x_k называют последовательностью приближений или итерационной последовательностью.

Последовательность приближений может быть как сходящейся, так и расходящейся.

Необходимое условие сходимости послед-ти {x_k}:

Пусть последовательность {x_k} сходится и функция а(ч) непрерывна, тогда последовательность сходится к корню ξ

Из сходимости => Сущ-ет lim x_k (при k -> ∞) = ξ

В (3) перейдем к пределу:

lim x_k (при k -> ∞) = lim f(x_k-1 )(при k -> ∞) = (непрерыв) f(lim x_k-1 (при k -> ∞)) =f(ξ)

ξ=f(ξ) и ξ- корень

Достаточные условия сходимости итерационного процесса выясняются следующей теоремой.

Пусть уравнение х=f(х) имеет единственный корень из отрезка [a; b] и выполнены условия:

1. f(х)определенна и дифференцируема на [a; b] ;

2. f(х)€[a; b]для всех x€[a; b] ;

3. существует такое вещественное число q, что |f '(х)|<=q<1 для всех х€[a; b].

Тогда итерационная последовательность x_n=f(x_n-1) (n=1, 2…) (4) сходится при любом начальном члене х₀€[a; b].

Доказательство.

Имеем x_n=f(x_n-1) (4)

Рассмотрим следующее приближение х_n+1=f(x_n).

По теореме Лагранжа о конечных приращениях имеем

х_n+1 - х_n=f(x_n)- f(x_n-1)=f '(c)(х_n-x_n-1), c€[х_n-1; x_n].

Переходим к модулям и принимая во внимание условие (3) теоремы, получим

|x_n+1-x_n|<=|f '(с)|· |x_n- x_n-1|<=q| x_n- x_n-1|,

|x_n+1- x_n|<= q| x_n - x_n-1|.

  При n=1, 2 … будем иметь:

|x₂-x₁|<= q| x₁ - x₀|,

|x₃-x₂|<= q²|x₁-x₀|, (6)

……………………

|x_n+1-x_n|<= qⁿ|x₁–x₀|.

Рассмотрим ряд

X₀+(x₁-х₀)+ (x₂-х₁)+…+ ( x_n - x_n-1)+… .(7)

Все члены ряда ограничены членами бесконечно убывающей геометрической прогрессии {qⁿ|x₁-x₀|}

Следовательно (7) сходится, причем абсолютно.

Имеем, раскрывая скобки в (7)

S_n+1 = x_n+1, где S_n+1 – частичная сумма ряда.

Из сходимости ряда следует, что существует lim S_n+1 (при n->∞) = ξ

Но lim S_n+1 (при n->∞) = lim х_n+1 (при n->∞) , т.е. последовательность {x_n} сходится.

Оценка погрешности метода

Пусть x_n— приближение к истинному значению корня уравнения ξ.

Имеем: x_n=S_n и ξ – сумма ряда (7)

Тогда обозначим через ∆x_n = |ξ-x_n| и ξ-x_n = (x_n+1-x_n)+(x_n+2-x_n+1)+…

∆x_n = |ξ-x_n| < = |x_n+1-x_n|+|x_n+2-x_n+1|+…< qⁿ|x₁-x₀| + qⁿ⁺¹|x₁-x₀| +… = qⁿ|x₁-x₀|(1+q+q²+…)= (геом прогрессия) qⁿ|x₁-x₀|*1/(1-q) = qⁿ/(1-q)*|x₁-x₀| (8)

На практике за начальное приближение можно выбрать х_n-1, а с учетом того, что qⁿ <=q, получим из (8)

∆x_n = q/(1-q)*|x_n-x_n-1| (9)

Пусть ε – требуемая точность. Тогда из (9) получим ∆x_n < q/(1-q)*|x_n-x_n-1| < ε и

|x_n-x_n-1| < ε(1-q)/q (10)

Неравенство (10 ) задает критерий остановок программы.