
Новая папка / № 23
.docРазноуровневое изучение тел вращения: определение, виды, свойства, построение, сечения плоскостью.
Как на базовом, так и на профильном уровне изучения математики при рассмотрении материала о телах вращения формального определения данного понятия не вводится.
Однако, в классах с углубленным изучением математики можно дать такое определение тела вращения: тело, образованное при вращении плоской ограниченной замкнутой фигуры вокруг прямой, лежащей в плоскости этой фигуры и не содержащей ее внутренних точек, называется телом вращения (Е. В. Потоскуев, Л. И. Звавич. Геометрия 10 класс: учебник для общеобразовательных учреждений с углубленным и профильным изучением математики).
То есть можно сказать, что изучение материала о телах вращения начинается сразу с рассмотрения конкретных видов тел вращения (цилиндра, конуса, шара, сферы).
ЦИЛИНДР

В общеобразовательных классах сначала дается определение кругового цилиндра, а после знакомства с такими его элементами, как основания и образующие, и прямого кругового цилиндра.
Цилиндром (точнее, круговым цилиндром) называется тело, которое состоит из двух кругов, не лежащих в одной плоскости и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов. Круги называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей кругов называются образующими цилиндра. Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований (учебник А.В.Погорелова).
Договариваются, что в дальнейшем будут рассматривать только прямой круговой цилиндр, называя его для краткости цилиндром.
После этого знакомятся с остальными элементами цилиндра - поверхность, высота, ось, радиус.
Поверхность цилиндра состоит из оснований и боковой поверхности. Боковая поверхность составлена из образующих.
Радиусом цилиндра называется радиус его основания.
Высотой цилиндра называется расстояние между плоскостями его оснований.
Осью цилиндра называется, прямая, проходящая через центры оснований.
Кроме этого с ребятами важно оговорить, что цилиндр может быть получен вращением прямоугольника вокруг одной из его сторон.
После чего для запоминания учащиеся знакомятся со свойствами цилиндра, которые даются с пояснениями:
-
Основания цилиндра равны, так как параллельный перенос есть движение.
-
У цилиндра основания лежат в параллельных плоскостях, так как при параллельном переносе плоскость переходит в параллельную плоскость.
-
У цилиндра образующие параллельны и равны, так как при параллельном переносе точки смещаются по параллельным прямым на одно и тоже расстояние.
Далее рассматриваются следующие сечения цилиндра плоскостью.
-
Если секущая плоскость проходит через ось цилиндра, то сечение представляет собой прямоугольник, две стороны которого – образующие, а две другие - диаметры оснований цилиндра. Такое сечение называется осевым.

-
Если секущая плоскость параллельна оси цилиндра, то в сечении получается прямоугольник.
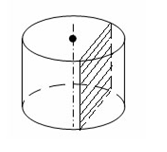
Доказывается теорема:
-
Плоскость, параллельная плоскости основания цилиндра, пересекает его боковую поверхность по окружности, равной окружности основания.
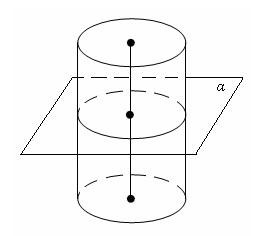
В классах с углубленным изучением математики, как правило, сначала дается общее определение цилиндрической поверхности и\иди цилиндра, а затем определение прямого и прямого кругового цилиндра.
Пусть
в некоторой плоскости
![]() задана
произвольная фигура
задана
произвольная фигура
![]() ,
не лежащая на одной прямой, и из точки
,
не лежащая на одной прямой, и из точки
![]() проведен
отрезок
проведен
отрезок
![]() ,
не лежащий в
,
не лежащий в
![]() .
Из каждой точки
.
Из каждой точки
![]() фигуры
фигуры
![]() проведен
отрезок
проведен
отрезок
![]() ,
параллельный и равный
,
параллельный и равный
![]() ,
который лежит по те же сторону от
,
который лежит по те же сторону от
![]() ,
что и отрезок
,
что и отрезок
![]() .
Фигура
.
Фигура
![]() ,
образованная всеми отрезками
,
образованная всеми отрезками
![]() ,
называется
цилиндром.
,
называется
цилиндром.
Цилиндр называется прямым, если его образующие перпендикулярны основанию.
Прямой цилиндр, основание которого круг, называется прямым круговым цилиндром (А.Д. Александров, А.Л. Вернер, В.И. Рыжик. Учебник для 10 класса школ с углубленным изучением математики).
После чего учащиеся также знакомятся с элементами цилиндра.
Кроме свойств цилиндра, рассматриваемых на базовом уровне, в профильных классах вводится такое свойство:
-
Все высоты цилиндра параллельны и равны друг другу.
Рассматриваются та же теорема и сечения, что и на общеобразовательном уровне. Дополнительно к этому
-
доказывается утверждение, что все сечения цилиндра плоскостями, параллельными плоскости основания, равны основаниям цилиндра и между собой;
-
вводится утверждение, что любое сечение прямого кругового цилиндра плоскостью, параллельной плоскости его основания, есть круг, а сечение его боковой поверхности – окружность этого круга;
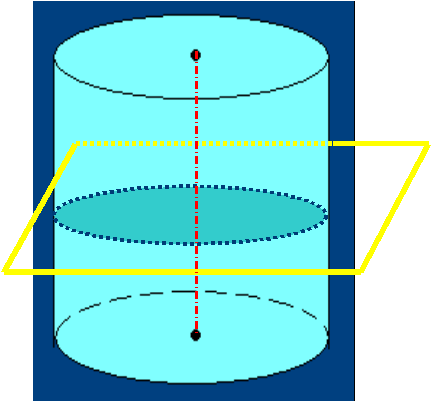
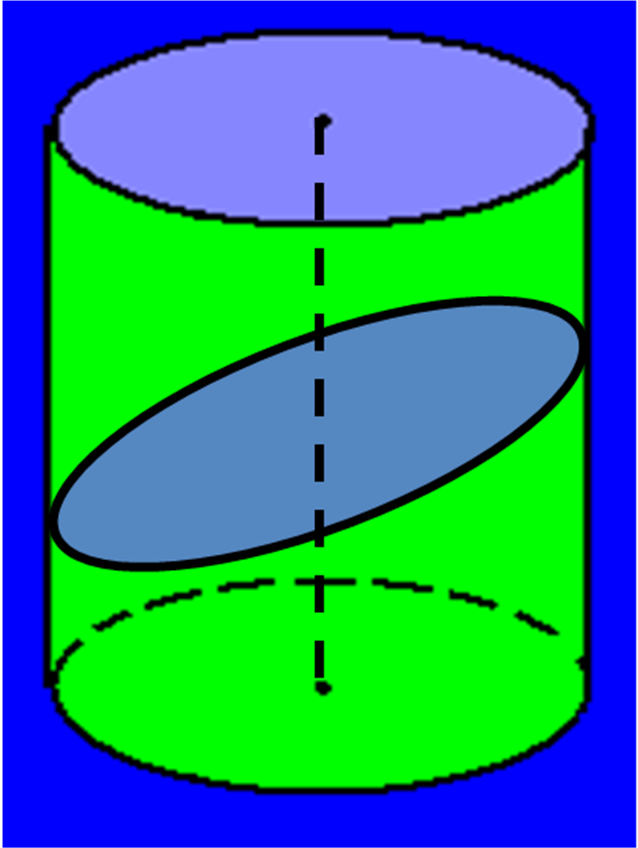
-
рассматривается сечение цилиндра плоскостью не параллельной ни основанию, ни образующим. В сечении получается эллипс.
Замечание: ни на базовом уровне, ни на профильном ничего не говорится о построении цилиндра.
КОНУС
Конус рассматривается по аналогичной схеме.
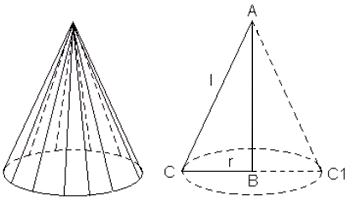
В общеобразовательных классах дается сначала определение кругового конуса и его образующих, а затем и определение прямого конуса.
Конусом (точнее, круговым конусом) называется тело, которое состоит из круга – основания конуса, точки, не лежащей в плоскости этого круга, - вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания. Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса.
Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания.
После этого знакомятся с остальными элементами конуса - поверхность, высота, ось.
Поверхность конуса состоит из основания и боковой поверхности.
Боковая поверхность составлена из образующих.
Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания, у прямого конуса основание высоты совпадает с центром основания.
Осью прямого кругового конуса называется, прямая, содержащая его высоту (учебник А.В.Погорелова).
Оговаривается, что конус может быть получен вращением прямоугольного треугольника вокруг одной из его сторон.
Никаких свойств конуса не рассматривается.
Рассматриваются следующие сечения конуса плоскостью.
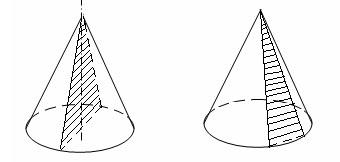
-
Если секущая плоскость проходит через ось конуса, то сечение представляет собой равнобедренный треугольник, основание которого диаметр основания конуса, а боковые стороны – образующие конуса. Такое сечение называется осевым.
-
Сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник, у которого боковые стороны являются образующими конуса.
Доказывается
теорема: плоскость, параллельная
плоскости основания конуса, пересекает
конус по кругу, а боковую поверхность
– по окружности с центром на оси конуса.
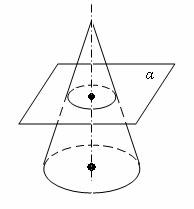
В классах с углубленным изучением математики, как правило, сначала дается общее определение конуса, а затем определение прямого кругового конуса.
Пусть
в некоторой плоскости задана какая-нибудь
фигура
![]() ,
не лежащая на одной прямой, а вне этой
плоскости - точка
,
не лежащая на одной прямой, а вне этой
плоскости - точка
![]() .
Фигура, образованная всевозможными
отрезками
.
Фигура, образованная всевозможными
отрезками
![]() ,
соединяющими точку
,
соединяющими точку
![]() с
точками фигуры
с
точками фигуры
![]() ,
называется конусом
с вершиной
,
называется конусом
с вершиной
![]() и
основанием
и
основанием
![]() .
.
Прямым круговым конусом или конусом вращения называется конус, основание которого - круг, а высота попадает в центр этого круга (А.Д. Александров, А.Л. Вернер, В.И. Рыжик. Учебник для 10 класса школ с углубленным изучением математики).
После чего учащиеся также знакомятся с элементами конуса.
Никаких свойств конуса не рассматривается.
Доказывается теорема (о сечении конуса). Пусть плоскость пересекает конус и параллельна плоскости его основания. Сечение конуса такой плоскостью подобно основанию конуса. Коэффициент подобия равен отношению расстояния от вершины конуса до плоскости сечения к высоте конуса.
Кроме сечений конуса плоскостью, рассматриваемых в общеобразовательных классах, на профильном уровне ещё можно рассмотреть сечения конуса плоскостью, когда в сечении получается эллипс (секущая плоскость пересекает все образующие конуса), парабола (секущая плоскость параллельна одной из образующих), гипербола (секущая плоскость параллельна двум образующим).
Изображение конусов.
Прямой круговой конус рисуют так. Сначала рисуют эллипс, изображающий окружность основания. Затем находят центр основания – точку О и вертикально проводят отрезок РО, который изображает высоту конуса. Из точки Р проводят к эллипсу касательные (опорные прямые) прямые (практически это делается на глаз, прикладывая линейку) и выделяют отрезки РА и РВ этих прямых от точки Р до точек касания А и В. Следует обратить внимание, что отрезок АВ – это не диаметр основания конуса, а треугольник АВР – не осевое сечение конуса. Осевое сечение конуса – это треугольник АРС: отрезок АС проходит через точку О. Невидимые линии рисуют штрихами; отрезок ОР часто не рисуют, а лишь мысленно намечают, чтобы изобразить вершину конуса Р прямо над центром основания – точкой О.
ШАР
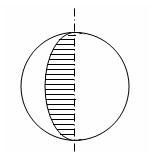
В общеобразовательных классах сначала дается определение шара, а затем сферы (шаровой поверхности).
Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии, не больше данного, от данной точки. Эта точка называется центром шара.
Граница шара называется шаровой поверхностью или сферой.
После этого рассматриваются элементы шара.
Любой отрезок, соединяющий центр шара с точкой шаровой поверхности, называется радиусом.
Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром.
Оговаривается, что шар можно получить при вращении полукруга вокруг его диаметра как оси, а сферу – полуокружности.
Рассматривают с доказательством теоремы:
-
Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость.
Плоскость, проходящая через центр шара, называется диаметральной плоскостью.
Сечение шара диаметральной плоскостью называется большим кругом, а сечение сферы – большой окружностью.
-
Любая диаметральная плоскость шара является его плоскостью симметрии. Центр шара является его центром симметрии.
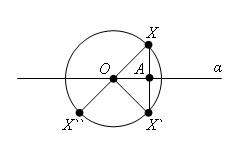
-
линия пересечения двух сфер есть окружность.
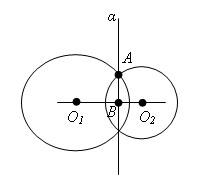
В классах с углубленным изучением математики, как правило, сначала дается определение сферы, а затем шара.
Сферой называется множество всех точек пространства, удаленных от данной точки, называемой центром, на одно и то же расстояние.
Отрезок, соединяющий любую точку сферы с ее центром, называется радиусом сферы.
Радиусом сферы называют также расстояние от любой точки сферы до ее центра.
Шаром называется множество всех точек пространства, расстояние от каждой из которых до данной точки - центра шара - не превосходит данного положительного числа, которое называется радиусом шара.
Доказывается теорема (о пресечении шара и сферы с плоскостью):
-
Если расстояние от центра шара до данной плоскости больше радиуса шара, то плоскость не имеет с шаром общих точек.
-
Если расстояние от центра шара до плоскости равно радиусу шара, то плоскость имеет с шаром и ограничивающей его сферой только одну общую точку.
-
Если расстояние от центра шара до плоскости меньше радиуса шара, то пересечение шара с плоскостью представляет собой круг. Центр этого круга находится в основании перпендикуляра, опущенного из центра шара на плоскость, или в самом центре шара, если плоскость проходит через центр. Пересечение плоскости со сферой представляет окружность указанного круга.
Построение шара.
Для построения достаточно ограничиться двумя-тремя пересекающимися образующими. Отложив от центра радиусы шара, проводят замкнутую кривую - контур шара.

