лабораторные на Pasca (Кудрявцев)l

74

Лабораторная работа № 7

ЦИКЛЫ

Циклы (многократно повторяемые действия) могут быть заданы в Turbo Pascal следующим образом:

a) Цикл со счетчиком:

for i := A to[downto] B do P

где i – переменная типа Integer; А и B – константы или выражения типа Integer; при to значение i при каждом повторе увеличивается на 1 (при А > В оператор Р не выполняется ни разу); при downto – уменьшается на 1 (при А < В оператор Р не выполняется ни разу); Р

–оператор (тело цикла),который может быть и составным:

for i := A to[downto] B do begin

<операторы>

end;

b) Цикл с завершением по нарушению условия:

while B do P;

где В – условие (при невыполнении условия оператор Р не выпол- няется ни разу); Р – оператор (тело цикла), который может быть и составным:

while B do begin

<операторы>

end;

Выполнение: проверяется условие В, и, если оно удовлетворено, то выполняется Р, а затем вновь проверяется В и т.д. Как только на очередном шаге окажется, что условие В не удовлетворяется, то выполнение цикла прекратится.

c)Цикл до выполнения условия (с завершением по достижению условия)

repeat <операторы>

i := 0; repeat

p := p i; i := i + 1 until i >= n;

write('n!=', p) End.

Пример 2. Составить программу, печатающую таблицу значений функции у=sqrt(x) на отрезке [0,3] с шагом 0,3.

Program t;

var i: integer; Begin

write('x', ' ': 6);

for i := 0 to 10 do write(i*0.3: 6: 1); writeln;

for i := 1 to 75 do write('-'); writeln;

write('sqrt(x)', ' '); for i := 0 to 10 do

write(sqrt(i*0.3): 6: 2) End.

Таблица будетизображена на экране в виде:

---------------------------------------------------------------------------------------------------

Пример 3. Не используя стандартные функции (за исключением abs), вычислить с точностью до 0.0001 функцию y=f(x). Считать, что требуемая точность достигнута, если очередное слагаемое по модулю меньше 0.0001, все последующие слагаемые можно уже не учитывать. Привести и значение функции у, найденное с помощью стандартных функций.

Program f1;

var x, y, n, u: real;

i := 0; s := 0; repeat

s := s + x; i := i + 1;

write('x', i + 1, '='); readln(x); until x < 0;

write('cp. арифм. =', s/i)

End.

Program s2;

var x, s: real; i: integer; Begin

write('x='); readln(x); i := 0; s := 0;

while x >= 0 do begin

s := s + x; i := i + 1;

write('x', i + 1, '='); readln(x) end;

write('cp. арифм. =', s/i)

End.

Пример 5. Дано целое n > 0. Составить программу, печатающую все простые числа из диапазона [2, n].

Program p1;

var n, m, k, p: integer; Begin

write('n='); readln(n); for m := 2 to n do

begin

p := 0;

for k := 2 to trunc(sqrt(m)) do if m mod k = 0 then p := 1;

if p = 0 then write(m,' ')

end

End.

Program p2;

var n, m, k: integer; t: boolean; Begin

write ('n='); readln(n); for m := 2 to n do

begin

k := 2; repeat

t := m mod k = 0; k := k + 1

until t or (k>= trunc(sqrt(m))); if not t then write (m, ' ')

end

end.

Недостатком программы р1 является неэкономное использование машинного времени: проверка на делимость делителем k каждый

раз осуществляется во всем диапазоне [2, 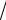m ].

В программе р2 выход из цикла организован с помощью булевой переменной t.

КОНТРОЛЬНЫЕ ЗАДАНИЯ

1. Сформировать таблицу значений функции у = f(x) на отрезке [a, b] с шагом h в виде:

3. Не используя стандартные функции (за исключением abs), вычислить с точностью до 0.0001 функцию y=f(x). Считать, что требуемая точность дос- тигнута, если очередное слагаемое по модулю меньше 0.0001, все последую- щие слагаемые можно уже не учитывать. Для задач 1) – 6) привести и значе- ние функции у, найденное с помощью стандартных функций.

4. Приближенно вычислить интегралы, используя метод средних прямо- угольников при n =100

b

ò f (x)dx = h[ f (x1 ) + f (x2 ) +K+ f (xn )],

a

7) – 9) – сравнить с результатомпредыдущего задания. 5. Вычислить:

1)Сколько членов суммы 1 + 1/2 + 1/3 + ... нужно взять, чтобы результат превысил 4?

2)Сколько членов суммы 1 + 1/4 + 1/9 + ... нужно взять, чтобы результат превысил 1.6?

3)Сколько членов суммы 1+1/2+1/4+1/8+1/16 + ... нужно взять, чтобы ре- зультатоказался не менее 1.999?

Числами Фибоначчи называют числа следующей последовательности: 1, 1, 2, 3, 5, 8, ... . Здесь каждое следующее число равно сумме двух предыдущих.

4)вычислить двадцатое число Фибоначчи;

5)вычислить сумму 10 первых чисел Фибоначчи;

6)найти первое число Фибоначчи, большее m (m > 1);

7)вычислить сумму всех чисел Фибоначчи, которые не превосходят 1000;

8)Вычислить сумму квадратов всех целых чисел, попадающих в интервал (ln x, ex), x > 1;

9)Вычислить количество точек с целочисленными координатами, попадаю- щих в круг радиуса r (r > 0) с центром в начале координат.

6. Решить следующие задачи:

1)Дано 15 вещественных чисел. Вычислить разность между максимальным и минимальным из них.

2)Дана непустая последовательность различных натуральных чисел, за кото- рой следует 0. Определить порядковый номер наименьшего из них.

3)Даны целое n > 0 и последовательность вещественных чисел, среди кото- рых есть хотя бы одно отрицательное число. Найти величину наибольшего среди отрицательных чисел этой последовательности.

4)Дано 12 вещественных чисел. Определить, образуют ли они воз- растающую последовательность.

5)Дана последовательность из 14 целых чисел. Определить, со скольких от- рицательных чисел она начинается.

6)Дано 15 вещественных чисел. Найти порядковый номер того из них, кото- рое наиболее близко к какому-нибудь целому числу.

7)Даны натуральное n и вещественные числа x1, у1, x2, у2, ..., xn, уn. Рассмат- ривая пары xk, уk как координаты точек на плоскости, определить радиус наименьшего круга (с центром в начале координат), внутрь которого попа- дают все эти точки.

8)Дана последовательность различных натуральных чисел, за которой следу- ет 0. Определить два наибольших числа среди них.

9)Дана последовательность различных натуральных чисел, за которой следу- ет 0. Определить, сколькоиз этих чисел больше предыдущего числа.