Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Алтайский государственный педагогический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

лабораторные на Pasca (Кудрявцев)l

.pdf

Скачиваний:

Добавлен:

18.03.2015

Размер:

1.63 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 394 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Составление линейных программ	33

программы обозначается служебным словом End, после которого ставится точка (End.).

В языке Turbo Pascal отсутствуют операторы ввода–вывода. Их роль играют процедуры Read, Readln, Write, Writeln, работа которых базируется на устройствах MS–DOS.

Процедура чтения Read обеспечивает ввод числовых данных, сим- волов, строк для последующей их обработки операторами програм- мы. Ее формат:

Read (FV, х1, x2, ..., хn);

где FV – имя устройства, откуда вводятся данные; х1, ..., хn – список идентификаторов вводимых переменных. По умолчанию FV равно CON (консоль), поэтому при вводе данных с клавиатуры FV можно не указывать.

Например:

Read(х,у);	{Вводятся значения переменных х и у}
Read(А);	{Вводится значение переменной А}

Вводимые значения набираются на клавиатуре минимум через один пробел и высвечиваются на экране. После набора данных для одной процедуры Read нажимается клавиша ввода (Enter).

Единственным отличием процедуры Readln от процедуры Read яв- ляется то, что после считывания значений всех переменных для од- ной процедуры Readln данные для следующей процедуры Readln будутсчитываться с начала новой строки.

В процедурах Read и Readln параметры можно не указывать:

Read;

Readln;

В обоих случаях вводится и отражается на экране произвольная строка символов. Ввод прекращается нажатием <Enter>.

Процедура вывода Write производит вывод числовых данных, сим- волов, строк и булевскихзначений. Формат:

Write(FV, y1, y2, ..., yn);

где FV – имя устройства, на которое осуществляется вывод.

34	Лабораторная работа № 2

По умолчанию FV равно CON (при выводе CON – экран); у1 , у2 , ..., уn – выражения, результаты выполнения которых выводятся на эк- ран, константы, имена переменных.

Процедура Writeln аналогична процедуре Write, но после вы- полнения происходит переходв начало следующей строки.

Например:

Write(55+66);

Write('Сумма 5 + 6 = ',5 + 6);

Writeln(x, y, Sum);

Форматированный вывод. В процедурах вывода на экран имеется возможность указать константу (или выражение), определяющую ширину поля вывода. Это значение указывается через двоеточие сразу после имени выводимой единицы:

Write(55+55:10,22:6); {результат:.......110....22}

(под число 110 отводится поле в десять позиций, под число 22 – в шесть).

Вещественные значения могут выводиться в форматах как с пла- вающей точкой, так и фиксированной точкой. В первом случае ука- зывается только ширина поля, во втором дополнительно фикси- руется количество символов в дробной части.

Например:

Write(655.04:15) {результат: 6.550400000Е+02}

Write(655.04:8:4) {результат: 655.0400}

Форматированный вывод позволяет оформлять выводимые данные в таблицы.

КОНТРОЛЬНЫЕ ЗАДАНИЯ

1.Составьте программы на языке Turbo Pascal для вычислений по фор- мулам:

1) y =

−ax +c

;

2) y =

c cos(

3x +b

;

x +c2

3x +c

4 + sin2 (x +b )

Составление линейных программ

(a2

+b 2 )x

x (a2 +b 2 )

y =

;

4) y =

;

a +b

e x sin

a +b

sin2 (x + y )+ cosx 2

z =

;

+ y 2e

x −y

x 2 +b

z = x -

;

b + sin2 (x

y )

y = (a + x )2 +a cos(a + x ) + a

;

a + x

u = sin (y -

)

y +b

x -

;

z 2 + x

9)y = sin 3px +tg 2 æç 3px + ap ö÷;

èø

ctg (x 2 +

);

10) y =

a +b

11) y = ln arctgx - sin(ax ) + 3ax ;

12) y = x	4	æ	x + p ö		;
12) y = x		ça sin 3x +bctg x - tg	c	÷	;
		è	c	ø

e x 2 ln

x 2 - x +c

+ 9x 3

;

13)

y =

2sin x

14)

u =

a + sin2 (x + y )

;

z +

x -

2bx a

z +

sin(x + y )

15)

y = ctg(4x + 3) + cos3

4x + 3

;

+e 2x +1 (x +b )ln

x +c

16)

y =

3 x 2

+ 4

;

x 2 - 3x

Лабораторная работа № 2

(

)

(

x 2

+1×e x

x 3

+ 2

x 2 + 1

17)

y =

)

;

ln(x 4 + e 2 )

18)

y = px

- x

2sinx

;

25)

y =

x 2 ln x

2 +

;

b + x

x 3

+ x 2 - 2x +c

19)

y = ln(x 2 +b )

(x -1)e x

;

26)

y =

tg3x

;

x 2 + e 2x

b +e −x ln

x 2 +

x 2 + 2x + 3

b ctg2 3x

20)

y = arcsin ç ln

;

27)

y = -

;

+ 2x

-c

21)

y =

+ ln

tg x

;

28)

y = (6x 2 - x + 2)

e −(x +4)

+ 4x 3

;

cosx

c +

e x sin

a +b

1+ x

x ln

x +

x 2 + 1

22)

y = -

a ctg x

;

29) y =

;

b cosx +c sin2 2x

x 2 +

x 3

23)

y =

x 2 - sin px

2 -ba

;

-e

cos

e x sin

30)

y =

x cos2x - x 2 sinx

x 2

- 3x +cb

24)

y =

;

b tg2 2x

Вычислить значения выражений:

1) 20 div 6;

20 mod 6;

2) 25 div 7;

25 mod 7;

3) 29 div 3;

29 mod 3;

4) 17 div 4;

17 mod 4;

5) 44 div 9;

44 mod 9;

6) 99 div 5;

99 mod 5;

7) 33 div 5;

33 mod 5;

8) 15 div 9;

15 mod 9;

9) 3 div 7;

3 mod 7;

10) 5 div 8;

5 mod 8;

11) 1 div 4;

1 mod 4;

12) 1 div 2;

1 mod 2;

13) 12 div 5;

12 mod 5;

14) 2 div 5;

2 mod 5;

15) 22 div 6;

22 mod 6;

16) 6 div 9;

6 mod 9;

17) 19 div 4;

19 mod 4;

18) 3 div 7;

3 mod 7;

19) 21 div 5

20 mod 7

20) 7 div 9

5 mod 9;

21) 23 div 7;

19 mod 6;

22) 9 div 11;

7 mod 11;

23) 25 div 9;

21 mod 8;

24) 11 div 13;

9 mod 13;

Составление линейных программ			37

25) 27 div 11;	23 mod 9;	26) 13 div 15;	11 mod 15;
27) 29 div 13;	25 mod 11;	28) 15 div 17;	13 mod 19;
29) 31 div 17;	27 mod 13;	30) 17 div 19;	15 mod 21.

3. Вычислить значения выражений:
1) – a mod b + a div be;	2) a mod b + ac div c
3) – ab div b mod c;	4) k mod n – k div c – 1;
5) c – b div (a + b) mod c;	6) a div be mod (ab);
7) a mod be + a div c;	8) ab mod ca div ba;
9) kn div a mod c;	10) a + b div (ab) + a mod b;
11) – ab mod cbc div a;	12) a mod b – (b – a) div cb;
13) k mod abc – c div ab;	14) kab div kab + a mod kb;
15) (k + b) mod kb div a + c;	16) a mod (a + b) c div ab;
17) ab div cb mod abc;	18) a + b mod kc + k div ab;
19) k div abc + ab mod kc;	20) nk div n – kn mod k + a;
21) a mod b div c mod a;	22) a – b mod ca + ca div b;
23) k mod (ab)c – c div a mod b;
24) b div ab mod c + b + c mod a;
25) k mod n + c + (a – b) div k;
26) (ab) mod (a + b) + ab mod cb;
27) (a + b) mod ab – a mod b div c;
28) k mod na – (k + a) div (b + k);
29) a mod b + c + (a + b) div ka;
30) a + b mod c + (a + b) div c.

Лабораторная работа № 3

ТИПЫ ДАННЫХ. ФУНКЦИИ ПРЕОБРАЗОВАНИЯТИПА

Любая константа, переменная, значение функции или выражения в Turbo Pascal характеризуется своим типом. Тип любого из этих объектов определяет множество допустимых значений, которые может иметь объект, а также множество допустимых операций, ко- торые применимы к объекту. Turbo Pascal характеризуется разветв- ленной структурой типов данных (рис.1).

	п	порядковые
т	п	порядковые
и	р	типы
п	о


ы	с
	т	вещественные
	т	вещественные
	ы	типы
	е
	е
	т
	и
	п
	ы

структурированные

типы

указатели

строки

процедурные

типы

целые типы

логический

тип

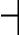символьный тип

перечисляемый

тип

тип - диапазон

массивы

записи

множества

файлы

объекты

Рис.1. Структура типов данных

Типы данных. Функции преобразования типа	39

Среди типов, используемых в языке, есть стандартные (предопреде- ленные) типы и типы, определяемые программистом.

Стандартные типы не требуют предварительного определения. Все

другие типы должны быть определены либо в разделе объявления типов, либо в разделе объявления переменных. В данной работе бу- дут описаны только простые типы данных.

Все простые типы, за исключением вещественных, называются по- рядковыми типами.

Для величин порядковых типов определены три стандартные функ-

ции: Odd, Pred, Succ.

Функция Odd(х) проверяет величину х на нечетность. Аргументом функции является величина типа Longint , результат равен True, ес- ли аргумент нечетный, и False – если четный.

Функция Pred(х) определяет предыдущее значение рассматривае- мой величины (например, Pred(2) равно 1).

Функция Succ(х) определяет последующее значение рассматри- ваемой величины (например, Succ(2) равно 3).

Функцию Pred(х) нельзя применять к первому элементу последо- вательности, а функцию Succ(х) – к последнему.

Целые типы. В Turbo Pascal имеется пять стандартных целых ти-

пов: Shortint, Integer, Longint, Byte, Word. Характеристика типов

приведена в таблице 1.

		Таблица 1

Тип	Диапазон	Формат
Shortint	–128..128	8–битовый знаковый
Integer	–32768..32767	16–битовый знаковый
Longint	–2147483648..2147483647	32–битовый знаковый
Byte	0..255	8–битовый беззнаковый
Word	0..65535	16–битовый беззнаковый

Над целыми числами определены операции: , +, –, div, mod. При использовании процедур и функций с целочисленными пара-

«Длинное целое», результатотносится к логическому типу.

40	Лабораторная работа № 3

метрами следует руководствоваться «вложенностью» типов, т.е. везде, где может использоваться Word, допускается использование Byte (но не наоборот). В Longint «входит» Integer, который, в свою очередь, включает в себя Shortint.

В таблице 2 содержится перечень встроенных процедур и функций, применимых к целочисленным типам:

		Таблица 2

Обращение	Тип результата	Действие
abs(х)	х	возвращает модуль х
chr(b)	char	возвращает символ, код которо-
		го равен b
dec(vx[,i])	как у vx	уменьшает значение vx на i,при
		отсутствии i – на 1
inc(vx[,i])	как у vx	увеличиваетзначение vx на i,
		при отсутствии i – на 1
odd(i)	boolean	возвращает True, если аргумент
		нечетное число; False, если
		четное
random	real	возвращает псевдослучайное
		число, равномерно распреде-
random(n)	integer	ленное на интервале 0 ≤ x <1
random(n)	integer	возвращает псевдослучайное
		возвращает псевдослучайное
		число, равномерно распреде-
		ленное на интервале 0 ≤ x < n
sqr (х)	как у параметра	возвращает квадрат аргумента

где b, w, i, l – обозначения соответственно типа Byte, Word, Integer, Longint; х – выражения любого из этих типов; vx – переменная; в квадратных скобках указан необязательный параметр.

При использовании разных целых типов в одном выражении они приводятся к базовому типу.

Например, при использовании Integer и Shortint базовым будет тип

Integer.

Типы данных. Функции преобразования типа	41

Логический тип. Стандартный логический тип Boolean представ- ляет такой тип данных, когда параметр может принимать два значе- ния True и False. При этом справедливы следующие условия:

false < true; ord(false) = 0; ord(true) = 1; succ(false) = true;

pred(true) = false.

Литерный (символьный) тип. Значением символьного типа Char является множество всех символов ПЭВМ. Каждому символу ПЭВМ предписывается целое число в диапазоне 0..255. Это число есть код внутреннего представления символа, его возвращает функция Ord. Для кодировки используется код ASCII (American Standard Code for Information Interchange). Первая половина символов с кодами 0..127

соответствует стандарту ASCII. Вторая половина символов с кодами 128..255 не ограничена жесткими рамками стандарта и может ме- няться на ПЭВМ разного типа. Во второй половине хранятся симво- лы национальных алфавитов, в том числе и русского языка. Симво- лы с кодами 0..31 относятся к служебным кодам.

К типу Char применима встроенная функция Chr(b), которая преоб- разует выражение типа Byte в символ и возвращает последний в ка- честве своего значения.

Перечисляемый тип. Перечисляемый тип определяется набором идентификаторов, с которыми могут совпадать значения парамет- ров. Список идентификаторов указывается в круглых скобках, идентификаторы разделяются запятыми. Объявление типа должно быть сделано в разделе объявлений, и ему должно предшествовать кодовое слово Type. Между значениями перечисляемого типа и по-

рядковыми номерами этих значений устанавливается следующее соотношение: первое значение в списке получает порядковый но- мер 0, второе – 1 и т.д. Максимальная мощность перечисляемого типа – 256 значений.

Пример 1.

Type

Operaс=(plus,minus,mult,divide);

Color=(black,white,blue,green,yellow,red,grey);

Month=(jan,feb,mar,apr,may,jun,jul,aug,sep,oct,nov,dec);

42	Лабораторная работа № 3

Логический и литерный типы являются частными случаями пере- числяемого типа, например:

Type

Boolean = (false, true);

Тип–диапазон. В любом порядковом типе можно выделить подмно- жество значений, определяемое минимальным и максимальным значениями. Такое подмножество определяет тип–диапазон. Объ- явление типа должно быть сделано в разделе объявлений типов.

Пример 2.

Type

Digit = –100..100;

Day = 1..31;

Ch = 'a'..'z';

Как видно из примеров, границы типа–диапазона разделяются спе- циальным символом – двумя последовательными точками (в отли- чие от принятого троеточия).

Вещественные типы. В Turbo Pascal имеется пять стандартных ве-

щественных типов: Real, Single, Double, Extended, Соmр. Харак-

теристики этих типов приведены в таблице 3.

			Таблица 3

Тип	Диапазон	Число	Размер в
Тип	Диапазон	значащих цифр	байтах
		значащих цифр	байтах
Real	2.9×10 – 39..1.7×1038	11 – 12	6
Single	1.5×10 – 45..3.4×1038	7–8	4
Double	5.0×10 –324..1.7×10308	15 – 16	8
Extended	3.4×10 – 4951..1.1×104932	19–20	10
Comp	–263 + 1..263– 1	19–20	8

Тип Comp фактически является типом целых чисел увеличенного диапазона, однако порядковым типом не является.

Доступ к типам Single, Double и Extended возможен только при осо- бых режимах компиляции. Эти типы рассчитаны на аппаратную поддержку арифметики с плавающей точкой и для их эффективно- го использования в состав ПЭВМ должен входить арифметический сопроцессор, что требует настройки компилятора.

<<< < Предыдущая 1 2 34 / 394 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.09.2019245.76 Кб4Курсовая 97.doc
#
08.12.201857.92 Кб3Курсовая по экономике Ч.Н.Е..docx
#
18.03.201571.2 Кб8КУРСОВАЯ.docx
#
27.09.2019251.17 Кб17Кутьмин. Освоение элементов актерского мастерст...rtf
#
16.11.2018129.02 Кб4лаборат. занятия по СРЯ.doc
#
18.03.20151.63 Mб32лабораторные на Pasca (Кудрявцев)l.pdf
#
18.03.201554.27 Кб14Лабы по ООП.doc
#
16.11.2019714.63 Кб6Лбова, Табарев. синкретизм.docx
#
18.03.201514.62 Кб10лексика.docx
#
27.10.20181.15 Mб85Лексические трудности при переводе (методичка).doc
#
18.03.2015238.61 Кб117Лекция 1. история телекоммуникаций.docx