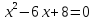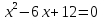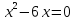Ответ: 20 см- ширина листа; 30 см- длина листа.

Пример 3. Тело брошено вертикально вверх со скоростью V₀=30 м/с. Через какое количество времени оно будет на высоте Н=40 м?

Решение.

Этап формализации. Перед решением задачи желательно повторить соответствующий материал из курса физики. Выясняется, что на рассматриваемое физическое явление существенное влияние оказывает скорость, с которой выполняется бросание: чем выше скорость, тем большей высоты тело достигнет.

С уроков физики учащимся известно, что движение тела брошенного вертикально вверх – равнозамедленное и подчиняется следующему закону:

, (1)

Где g- ускорение свободного падения тела,.

Уравнение (1) является математической моделью решаемой физической задачи.

Этап исследования построенной модели сводится к решению уравнения (1) относительно t.

После подстановки и преобразований получим уравнение: t² -6t+8=0. Корнями этого уравнения являются числа 2 и 4.

Этап интерпретации результатов заключается в переводе решения уравнения (1) на язык исходной физической задачи.

Корни уравнения t₁=2 и t₂=4 показывают, что тело будет на высоте в 60 м два раза, через 2 с и через 4 с после начала движения.

После решения этой задачи целесообразно провести с учащимися следующую исследовательскую работу.

Изменяя условия задачи, учитель может привести примеры квадратных уравнений, которые имеют два корня, не имеют корней или имеют корни с противоположными знаками, и выявить физический смысл этих решений.

Рассмотрим таблицу:

№	Н, м	Уравнение	Корни	Вывод
1	40		2 и 4	На уровне 40 м тело окажется два раза.
2	45		3 и 3	Наибольшая высота подъема 45 м.
3	60		Нет действительных корней	Высоты в 60 м тело не достигнет.
4	0		0 и 6	Тело брошено из исходного положения.

Таблица 1

Пример 4. Нефтяная компания ежедневно отправляет на свои автозаправочные станции 120 000 л бензина (равное количество на каждую станцию). Подсчитано, что в выходные дни выгоднее четыре автозаправки закрывать, а предназначенный для них бензин распределять (в равной мере) среди остальных. При этом каждая автозаправка увеличит количество реализуемого бензина на 8 000 л (это их предельная вместимость). Сколько автозаправочных станций имеет нефтяная компания? Какова вместимость каждой автозаправки.

Решение. Опишем текстовую модель данной экономической задачи.

Этап 1. Обозначим через х – количество автозаправочных станций, которыми владеет нефтяная компания, тогда 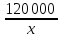- количество реализуемого бензина на каждой автозаправке в обычные дни, а

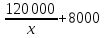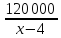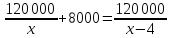– в выходные дни. Так как в выходные дни не работают четыре автозаправки, то - количество бензина, реализуемого на работающих автозаправках в выходные дни. Исходя из описанных условий составим уравнение:, (3)

Уравнение (3) является математической моделью исходной экономической задачи.

Этап 2. После выполнения преобразований уравнение (3) примет вид: 120 000(x-4)+8000·x(x-4)=120 000x. После выполнения тождественных преобразований получаем следующее квадратное уравнение: x²-4x-60=0, отсюда x₁=-6 и x₂=10.

Этап 3. Исходя из полученных результатов, в соответствии с условием задачи нефтяная компания имеет 10 автозаправочных станций, предельная вместимость каждой из которых равна: (л).

Пример 5. Из круглого бревна, толщина которого d см, следует вырезать балку прямоугольного сечения. Прочность балки пропорциональна ab² (a, b – измерения сечения балки в см). При каких значениях a и b прочность балки будет наибольшей.

Решение.

Прежде чем приступить к решению задачи, учащимся следует пояснить, что под толщиной круглого бревна понимается диаметр его более тонкого конца. Факторами на прочность балки являются диаметр бревна, форма и размеры сечения, вид древесины, из которой балка изготовлена (но при решении задачи эти условием можно пренебречь).

Этап формализации. Обозначим прочность балки через Р, а коэффициент пропорциональности через k (k>0). Из курса физики известно, что P=kab². Тогда математическая задача может быть сформулирована следующим образом: «При каких значениях переменных a и b функция Р принимает наибольшее значение? ». Выполним чертеж (рис.9)

Пусть АВ=b, AD=a, BD=d, тогда b²=d²-a² .

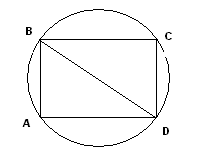
Отсюда получаем, P(a)=ka(d²-a²) (4), причем

a(0;d). Уравнение (4) –математическая модель приведенной задачи.

Рис.9

Этап исследования построенной модели. Для нахождения решения математической задачи найдем производную функции представленной в уравнении (4) . Найдем критические точки функции: 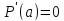, 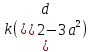=0, получим:

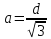или 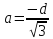, так как a(0;d), то не удовлетворяет условию задачи. Таким образом, на заданном интервале функция 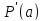имеет одну критическую точку

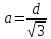
0 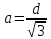d (Рис. 10)

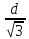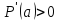При а (0;) , значит функция Р(а) возрастает на (0;),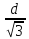

при а (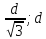) , значит функция Р(а) убывает на (). Таким образом, так как функция Р(а) непрерывна на заданном промежутке и имеет на нем один экстремум, точку максимума, то в этой точке функция достигает своего наибольшего значения. Из равенства b²=d²-a² получаем, что 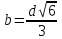. Значит функция Р принимает наибольшее значение пр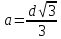и и .

Этап интерпретации результатов. Исходя из найденных значений переменных a и b, получаем, что прочность балки составляет .

После того как решение исходной задачи завершено, целесообразно сделать следующий вывод:

Если размеры прямоугольного сечения будут отличны от оптимальных, то прочность балки уменьшается, при этом она может не выдержать нагрузки, либо срок ее службы будет гораздо меньше, что экономически невыгодно.

В данном случае учащимся можно предложить следующую исследовательскую работу:

Будем варьировать значения переменных a и b.

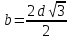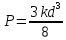1. При a=, . Прочность балки , по сравнению с наибольшей уменьшится на 2,5%.

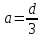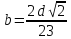2. При , . Прочность балки составит 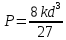и будет меньше наибольшей прочности на 23,1%.

3. При , 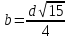прочность балки 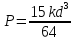. Такая прочность меньше наибольшей на 39,1%. Школьникам следует пояснить, что уменьшение прочности балки при размерах прямоугольного сечения, отличных от оптимальных может привести к уменьшению срока ее службы, либо балка не выдержит нагрузки, а с экономической точки зрения это невыгодно.

14