Задача 5

Вывести формулу для определения длины стрелы автомобильного крана, с помощью которого можно построить здание высоты Н и ширины 2c плоской крышей.

Решение:

Так как автомобильный кран может перемещаться вокруг всего здания, то крюк его крана достанет до любой точки здания, если он достанет (рис. 5) до середины крыши (имеется в виду середина по ширине).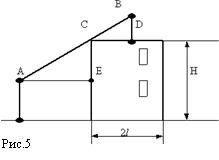

Рассмотрим кран, который находится в точке О, подает деталь на середину крыши. Пусть угол наклона стрелы при этом составляет . Тогда BC= =; AC = =, где h = АО – высота подвеса стрелы крана. В таком случае длина стрелы крана +(1)

Из формулы (1) видно, что для совершения указанной работы краном, установленным в другой точке (ближе к зданию или дальше от него), потребуется кран с другой длиной стрелы, поскольку при таком перемещении меняется угол . Определим наивыгоднейшее место установки крана, т.е. такое место, с которого заданная работа может быть выполнена краном с наименьшей длиной стрелы. Для этого, очевидно, достаточно определить, при каком, из промежутка (0;) функция l принимает наименьшее значение.

Найдем производную функции

Производная обращается в нуль лишь в одной точке ₀= arctgи функция l достигает своего наименьшего значения при ₀= arctg.

Найдя из полученной формулы значение ₀ и подставив его в формулу (1), мы и получим наименьшее возможное значение стрелы. Эти формулы и используются на практике.

Деревообработка. Важное народнохозяйственное значение имеет рациональный раскрой древесины. Комплексное решение таких задач требует применения довольно глубоких методов классической и современной математики. Однако отдельные задачи такого рода можно решить, используя только производную.

Задача 6

На лесопильных рамах (они предназначены для продольного пиления) бревна часто распиливают на квадратный брус и четыре доски (рис. 9) с максимально возможной площадью поперечного сечения. Какой должна быть расстановка пил для такой распиловки?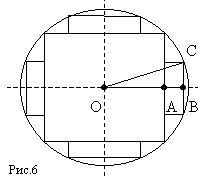

Решение:

Из рис. 6 видно, что для ответа на вопрос задачи достаточно определить толщину выпиливаемых досок. Так как сторона квадрата, вписанного в окружность радиуса r, равна r, то ОА = . Пусть толщина доски АВ = х, тогда ее ширина 2ВС = =, а площадь поперечного сечения:

S(x) = 2= .Требуется узнать, при каком х из отрезка [0;] функция S достигает наибольшего значения.

Найдем производную : S'(x) =.

Критическая точка: x₀=Так как S(0) = S, а S(x₀)' > 0, то доски толщиной 0,10d имеют наибольшую площадь поперечного сечения.

Ответ: 0,10d.

Сельское хозяйство. Усилению политехнической и трудовой направленности обучения математике способствует решение задач практического характера. Многие из этих задач сводятся, как известно, к нахождению наибольшего или наименьшего значения функции на некотором промежутке.

Задача 7

Пастбищные водопоильные желоба для коров иногда устраивают из трех одинаковых досок, сбивая их под некоторым тупым углом величины . Каким должен быть угол , чтобы получился желоб наибольшей вместимости? (рис. 7)

Решение:

Обозначим через х величину угла BAD, а через h ширину досок, тогда

АВ = ВС = CD = h, AE = hcosx, AD = h + 2hcosx, BE = hsinx.

Желоб представляет собой призму, основанием которой служит трапеция ABCD, а высота равна длине сбиваемых досок. Обозначив длину досок через l, найдем объем желоба. V(x) = l h² (1+cosx)sinx. Требуется узнать при каком значении х из интервала (0; ) функция V принимает наибольшее значение.

Найдем производную функции V:

V' = l h²(cosx(l + cosx) – sin²x) = l h² (2cos²x + cosx – 1) =2 l h² (cosx – )(cosx +1),

замечаем, что на рассматриваемом интервале производная существует и обращается в нуль только при х = , причем при 0 < х < производная положительна, а при < х < отрицательна. Значит, функция V достигает своего наибольшего значения на интервале (0; ) при х = .

Зная оптимальное значение x, найдем искомое значение α:

.

Ответ:

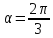
Приложение 2

Задачи, решаемые методом математического моделирования

Пример 1. В арифметической прогрессии второй член равен 6. При каком значении d<2, произведение первого, третьего и шестого членов арифметической прогрессии будет наименьшим.

Решение.

Этап 1. Известна формула для нахождения n-го члена арифметической прогрессии a_n=a₁+d(n-1). Найдем, первый, третий и шестой члены исходя из того что а₂=6: a₁=6-d; a₃=6+d; a₆=6+4d.

Обозначим через S- произведение a₁, a₃ и a₆, получим

S=(6-d)·(6+d)·(6+4d)=(36-d²)·(6+4d)=216-6d²+144d-4d³ при условии d<2

Уравнение S=-4 d³ -6d²+144d+216 является математической моделью представленной алгебраической задачи.

Этап 2. Найдем производную функции S: S’=-12d²-12d+144.

S’=0, -12d²-12d+144=0,

d²+d-12=0, отсюда d=3 или d=-4.

Этап 3 . Так как по условию задачи d<2, то, исходя из полученных результатов делаем вывод, что d=-4.

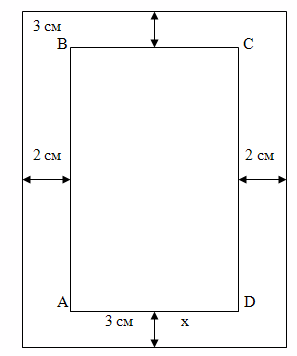
Пример 2. На бумаге текст должен занимать 384 см². Верхнее и нижнее поля должны быть по 3 см, а левое и правое по 2 см. если учитывать только экономию бумаги, то каковы должны быть наиболее выгодные размеры страницы?

Решение:

Этап 1. Пусть длина печатного текста будет х см, причем 0<х<384, а его ширина составляет 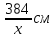. Значит размеры страницы будут соответственно равны (х+4) см и 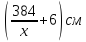. Тогда площадь страницы составляет 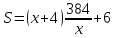, (1). Уравнение (1) является математической моделью данной задачи.

Рис.8

Этап 2. Выполнив преобразования в уравнении (1), получим

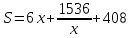. Найдем производную S(x):

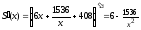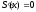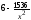, при =0 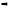6х²=1536 х₁ = 16 или х₂ = - 16 (0;384).

Этап 3. Итак, размер листа должен быть 16+4=20 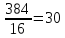(см), (см).